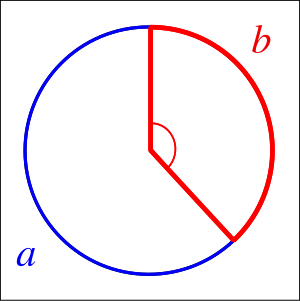Différences entre versions de « Nombre d'or »
(illustration du nombre d'or) |
(déplacement images) |
||
| Ligne 4 : | Ligne 4 : | ||
== Définition == | == Définition == | ||
| − | + | [[Fichier:Golden ratio line2.svg|vignette]] | |
Le nombre d'or est une proportion, définie initialement en géométrie comme l'unique rapport a/b entre deux longueurs a et b telles que le rapport de la somme a + b des deux longueurs sur la plus grande (a) soit égal à celui de la plus grande (a) sur la plus petite (b). | Le nombre d'or est une proportion, définie initialement en géométrie comme l'unique rapport a/b entre deux longueurs a et b telles que le rapport de la somme a + b des deux longueurs sur la plus grande (a) soit égal à celui de la plus grande (a) sur la plus petite (b). | ||
| Ligne 14 : | Ligne 14 : | ||
C'est pour cette raison que ce rapport est souvent appelé: La divine proportion. | C'est pour cette raison que ce rapport est souvent appelé: La divine proportion. | ||
| − | + | ||
== Valeur du nombre d'or == | == Valeur du nombre d'or == | ||
| + | [[Fichier:Rectangles d or.svg|vignette]] | ||
Ce nombre irrationnel est l'unique solution positive de l'équation x^2 = x + 1. Il vaut exactement (1+√5)/2 | Ce nombre irrationnel est l'unique solution positive de l'équation x^2 = x + 1. Il vaut exactement (1+√5)/2 | ||
| Ligne 25 : | Ligne 26 : | ||
φ = (1 + √5)/2 = 1/2 + √5/2 ≈ 1.61803398875 | φ = (1 + √5)/2 = 1/2 + √5/2 ≈ 1.61803398875 | ||
| − | + | ||
== Équations remarquables == | == Équations remarquables == | ||
| Ligne 60 : | Ligne 61 : | ||
== Suite de Fibonacci == | == Suite de Fibonacci == | ||
| + | |||
| + | [[Fichier:Fibonacci spiral 34.svg|vignette]] | ||
La suite de Fibonacci a été découverte par Léonardo Fibonacci en étudiant la croissance des générations de lapins. | La suite de Fibonacci a été découverte par Léonardo Fibonacci en étudiant la croissance des générations de lapins. | ||
| Ligne 74 : | Ligne 77 : | ||
La nature utilise fréquemment la suite de fibonacci comme base de construction. (pétale, pomme de pin, etc..) On appelle ceci de la phyllotaxie. | La nature utilise fréquemment la suite de fibonacci comme base de construction. (pétale, pomme de pin, etc..) On appelle ceci de la phyllotaxie. | ||
| − | |||
== Angle d'or == | == Angle d'or == | ||
Version du 27 janvier 2021 à 00:21
L'article wikipedia sur le Nombre d'Or étant déjà jugé comme un bon article, pour éviter de réinventer la roue, il est déjà possible de se référer à cet article.
Le nombre d'or est aussi fréquemment appelé du nom de la lettre grecque Phi, Φ, φ, 𝜑
Définition
Le nombre d'or est une proportion, définie initialement en géométrie comme l'unique rapport a/b entre deux longueurs a et b telles que le rapport de la somme a + b des deux longueurs sur la plus grande (a) soit égal à celui de la plus grande (a) sur la plus petite (b).
C'est à dire lorsque (a+b)/a = a/b
Voici la même définition avec d'autres mots: Trois points alignés, déterminant deux segments forment une section dorée (un rapport égal à Phi), s'il y a de la petite partie à la grande, le même rapport que de la grande au tout.
Le nombre d'or est le seul rapport qui met en résonance la partie avec le tout. On peut donc le voir comme étant une résonance (fractale) entre la créature et son créateur.
C'est pour cette raison que ce rapport est souvent appelé: La divine proportion.
Valeur du nombre d'or
Ce nombre irrationnel est l'unique solution positive de l'équation x^2 = x + 1. Il vaut exactement (1+√5)/2
Soit environ 1.6180339887
Une nombre irrationnel est un nombre qu'il n'est pas possible de réduire en ratio. Soit en fraction. Contrairement à π, phi n'est pas un nombre transcendant (un nombre transcendant n'est racine d'aucune équation polynomiale)
φ = (1 + √5)/2 = 1/2 + √5/2 ≈ 1.61803398875
Équations remarquables
On peut déduire plusieurs particularités de cette équation:
φ² = φ + 1 ≈ 2.6180339887
1/φ = φ - 1 ≈ 0.6180339887
√5 = φ + 1/φ ≈ 1.6180339887 + 0.6180339887 ≈ 2.236067977
Progression géométrique et arithmétique
Grâce aux équations remarquable ci-dessus, le nombre d'or est certainement le seul nombre pour lequel on peut faire coïncider une progression géométrique et une progression arithmétique.
| x-3 | x-2 | x-1 | 0 | x1 | x2 | x3 |
|---|---|---|---|---|---|---|
| 1/φ3 | 1/φ² | 1/φ | 1 | φ | φ² | φ3 |
| 0.235 | 0.382 | 0.618 | 1 | 1.618 | 2.618 | 4.236 |
La progression géométrique s'obtient en augmentant la puissance (comme sur l'exemple théorique de la première ligne. La deuxième ligne montrant concrètement ce que ça donne dans le cas de Phi) Le résultat approché est indiqué en notation à virgule sur la troisième ligne.
La progression arithmétique s'obtient en additionnant deux nombres successifs de la suite pour trouver le suivant.
Par exemple: 0.618 + 1 = 1.618 => 1.618 + 1 = 2.618 ... etc.
Attention, sur la 3ème ligne se sont des valeurs approchées, l'exemple d'addition marche bien, car c'est le moment de la suite où le chiffre 1 intervient et qu'il est donc facile de l'additionner. Pour les autres il faut utiliser la valeur exacte.
Suite de Fibonacci
La suite de Fibonacci a été découverte par Léonardo Fibonacci en étudiant la croissance des générations de lapins.
La suite de Fibonacci est une suite d'entiers dans laquelle chaque terme est la somme des deux termes qui le précèdent. Elle commence généralement par les termes 0 et 1 (parfois 1 et 1) et ses premiers termes sont: 0, 1, 1, 2, 3, 5, 8, 13, 21, etc.
Les quotients de deux termes consécutifs de la suite de Fibonacci sont les meilleures approximations du nombre d'or. 0 1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597 2584 4181 6765 10946 17711 …
C'est à partir du quotient de 144/89 que l'approximation atteint la précision qui est couramment utilisée du nombre d'or.
144/89 = 1.617977
La nature utilise fréquemment la suite de fibonacci comme base de construction. (pétale, pomme de pin, etc..) On appelle ceci de la phyllotaxie.
Angle d'or
L'angle d'or est similaire, mais pour un angle. On retrouve ceci pour le positionnement des feuilles sur la tige de nombreuses plantes. L'avantage est d'utiliser l'irrationalité du nombre d'or. Si je pose une feuille à chaque rotation de l'angle d'or je ne vais jamais retomber exactement au dessus d'une autre feuille. Ainsi je maximise le captage solaire. (si j'utilise des fractions entières ça ne marche pas. Par exemple si je tourne d'un quart de tour.. je vais retomber sur la même feuille chaque 4 feuilles.)
L'angle d'or vaut: 137,51°. (et son complément 222,49°)
On retombe ainsi sur le fameux nombre 137.
L'alignement central des menhirs de Clendy a un azimut de 222° ... C'est la marque que les bâtisseurs de mégalithes utilisaient ces propriétés de géométrie sacrée.