Chambre de Khéops
La chambre haute de la grande pyramide, la chambre du roi ou chambre de Khéops.
Voici ce qu'on trouve sur wikipedia... https://fr.wikipedia.org/wiki/Chambres_et_couloirs_de_la_pyramide_de_Kh%C3%A9ops#La_chambre_du_roi
Les mesures de Flinders Petrie: http://www.ronaldbirdsall.com/gizeh/petrie/c7.html (point 52)
La chambre est en Syénite, une sorte de granite qui ne continent PAS de quartz.
https://fr.wikipedia.org/wiki/Sy%C3%A9nite
Tous les images des frères morton en 1910...
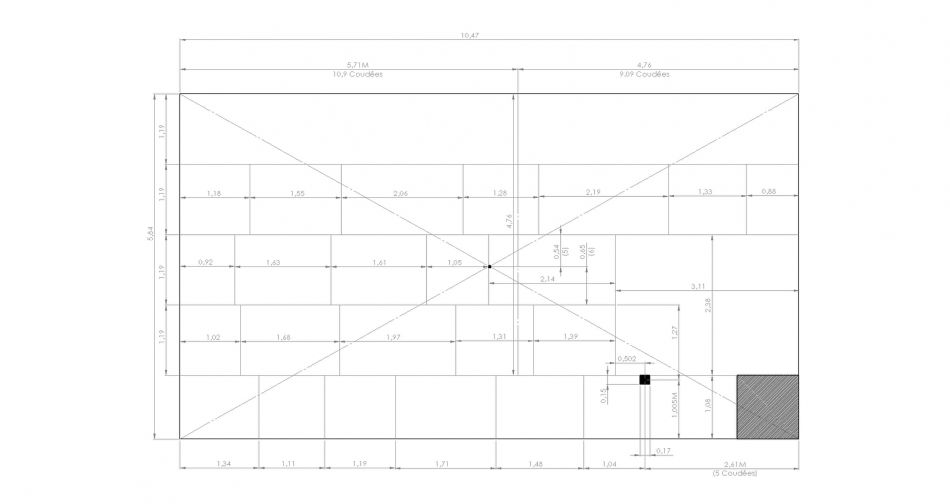
Plan de la chambre du Roi de la pyramide de Khéops
Voici le plan selon les mesures de Gilles Dormion redessiné par l'apprenti-sage.
Vitesse de la lumière dans la chambre haute ?
https://larazzodeltempo.it/2021/camera-re-scoperta/
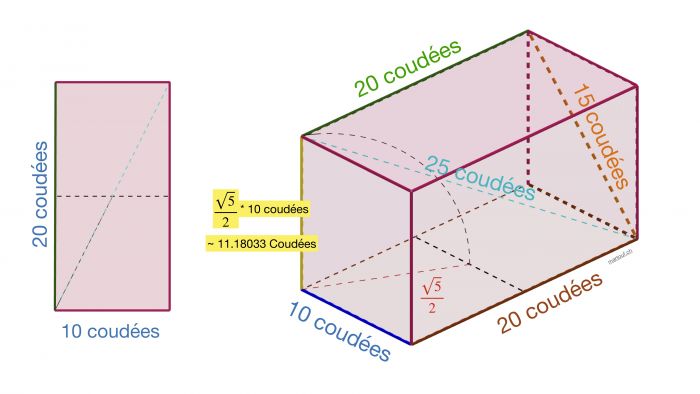
La géométrie de la chambre
La géométrie de la chambre montre un bi-carré et en volume un triangle 3-4-5.
En astro-géométrie, Le bi-carré étant typique du rectangle solsticial de Karnak et le triangle 3-4-5 du rectangle solsticial de Carnac.
Avec ce chambre on a le lien entre les deux.
Voici le moment précis d'une explication de Howard Crowhurst sur le sujet: https://www.youtube.com/watch?v=6kIKeA3PmMQ&feature=youtu.be&t=4818
on marque les diagonale du bi-carré..
On relève la moitié de la diagonale... et hop on a la hauteur !
- √ 5 = diagonale
- √ 5 / 2
On peut aussi faire un bi-carré vertical dans la hauteur...
Georges Juvenne.. architecte des monuments historique.
Diagonale du mur du fond ( le carré. Le mur proche de l'entrée ou celui proche du sarcophage) = 3/2
→ on élimine la racine !! (√ 5/2)^2 + 1^2 = 5/3 + 4/4 = 9/4 → √9/4 = 3/2
si on prend la grande diagonale en volume.... on a un triangle 3-4-5 → diagonale = 5/2 (côté = 2= 4/2 et voir ci-dessus diagonale du carré = 3/2)
Mesures de la chambre de Khéops par Flinders Petries
Flinders Petrie a mesuré la chambre dans toutes les dimensions et à plusieurs niveau. Ses mesures sont en pouce (2.54 cm)
Ce livre est aussi disponibles en format web (ocr) ici: http://www.ronaldbirdsall.com/gizeh/petrie/c7.html (point 52 pour la page sur les mesure de la chambre de Kheops)
|
|
N. |
N.E. |
E. |
S.E. |
S. |
S.W. |
W. |
N.W. |
|
Top |
412.14 |
+ 0' 4" |
206.30 |
– 0' 35" |
411.88 |
+ 1' 35" |
206.04 |
– 1' 4" |
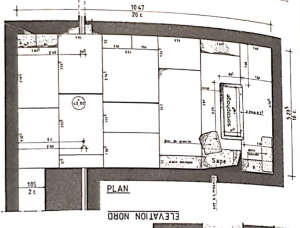
Plan de Gilles Dormion
En 1988 L'architecte Français Gilles Dormion a participé à l'installation d'une ventilation dans la pyramide de Khéops. A cette occasion il a pu accéder à pas mal d'endroit et il a fait des plans. On trouve dans son livre de 1998 des plans qu'il a réalisé en 1996 (d'après le cartouche du plan).
Il y a un passage du livre qui dit qu'il utilise la coudée de 52,35 cm mesurée par J. Dorner. Donc c'est étonnant, est-ce que Gilles Dormion a fait ses propres mesures ou est-ce qu'il a repris les mesures de Dorner pour faire ses plans ?
On voit la longueur de 10,47 mètre, de la chambre ce qui correspond en effet à une coudée de 52,35 cm.
Livre de Gilles Dormion: la Chambre de Chéops, Analyse architecturale....
Gamme musicale
Selon Stéphane Cardinaux dans géométrie sacrée tome 2 p286
La chambre haute donne des dimensions qui permettent de construire une gamme diatonique de ptolémée avec une bonne précision.
→ soit aussi gamme naturelle..
- 20/10 = 2.000 = DO (0%)
- 20/11.18 = 1.789 ≈ SI (4.5%)
- 25/15 = 1.666 = LA (0%)
- 15/10 = 1.500 = SOL(0%)
- 20115 =1.333 = FA (0%)
- 25/20 = 1.250 = MI (0%)
- 11.18/10 = 1.118 ≈ RE (0.6%)
Pour entendre ce que ça donne, voici un petit aperçu de cette gamme dans le générique des vidéeo de l'apprenti-sage..
Tracé régulateur selon Stéphane Cardinaux:
A la p.285 il présente un tracé régulateur de la grande pyramide. Il trouve que la chambre haute se positionne à 3cm près sur son tracé.
Il ajoute un rectangle sacré inscrit dans le triangle de la coupe de la pyramide. Ce rectangle montre les prolongements des "canaux de ventilation" de la chambre du roi. Il fait ensuite un double carré inscrit verticalement depuis la droite et ainsi positionne la base de la chambre.
Positionnement de la chambre dans la pyramide
Ce dessin montre que l'on peut inscrire la pyramide dans un rectangle d'or où le grand côté est l'arrête....
- de là on voit que la diagonale du rectangle d'or passe par la chambre du roi....
- de là on voit que la diagonale du carré de construction du rectangle d'or passe aussi par la chambre du roi....
- les 2 diagonales se croisent !
- on a donc là un effet de résonance en ce lieu... mais pas un tracé directeur.
Dans le film LRDP à 58min 18, il est dit:
- h = la hauteur visible
- h/2 = le sommet des chevrons de la chambre haute
- h/3 = le plafond de la chambre haute
- h/4 = le sommet de chevron de la chambre médiane
- h/5 = le plancher de la chambre basse
- h/7 = le plancher de la chambre médiane
Selon Quentin Leplat, il y a un triple carré qui permet de positionner la chambre haute. https://www.youtube.com/watch?t=1111&v=SXNNVbDTIrM
Le triple carré est aussi ici: c'est 82 coudée de haut... et donc 246 de large pour atteindre le côté le plus éloigné du bord de la pyramide.
Voir le dessin ici: http://www.cerclesdanslanuit.com/pi.php
Il existe une relation remarquable entre l'aire de la base de la pyramide et l'aire du niveau de la chambre du roi, dont le sol se situe à 82 coudées (Gilles Dormion, La Chambre de Chéops, 2004) au-dessus du niveau du sol. L'aire de la base vaut 440^2 coudées^2, soit 193 600 coudées^2 soit encore 2×96 800 coudées^2. Les côtés du niveau de la chambre du roi valent 2×(220 – 82×11/14) = 311,14 coudées. L'aire de ce niveau est donc égale à 96 809,88 coudées^2. Première propriété : l'aire du niveau de la chambre du roi est égale, à 0,01 % près, à la moitié de l'aire de la base de la pyramide.
A creuser...
guasco p230
La hauteur du sol de la chambre haute est égale à la différence de hauteur entre le triangle (phi) de la pyramide et le triangle idéal équilatéral. Ce qui équivaut pour lui a une énergie ! ... car il associe le côté du triangle à espace-temps et masse pour le côté au sol. (Modifier un des facteurs crée une énergie... en physique nucléaire on modifie des masses pour avoir de l'énergie... en balistique on utilise l'espace et le temps... soit la vitesse... L'alchimiste ne touche que le temps !)
Ce que je ne comprends pas c'est qu'au schéma suivant cette hauteur se retrouve dans les chambres de décharge de la chambre haute !!
Sarcophage
Sarcophage est un mot grec qui signifie "mangeur de chair"... c'est pas tout à fait pareil que le mot égyptien neb-ankh qui est le panier de vie. Voir cette conférence => https://www.youtube.com/watch?v=QcgoXyGToWY
Cette boite est-elle donc pour y mettre un mort ou pour donner la vie ?
Selon Roger Guasco:
La rosée brûle le SEL de Roger Gusaco. (pdf)
Il ne faut pas oublier de parler du coffre de la Chambre du Roi: Sa longueur extérieure mesure officiellement 2,292 m et la longueur intérieure 1,985 m. Si l'on calcule le rapport entre ces deux dimensions, on retrouve 115,47 !
La demi-longueur, 2,292 : 2, est égale à 1,146, dimension que l'on retrouve dans la pyramide dite intérieure. Le retrait des parois, étant de 0,866, on s'aperçoit alors que 114,6 + 0,866 = 115,466 (PLAN 9, Fig. A). p227-228
0,866 = √ 3 / 2 = cos π /6
http://www.ronaldbirdsall.com/gizeh/petrie/c2.html Pétrie:
- Extérieur : longueur de 2,2764m ± 5 mm, largeur de 97,8 cm ± 2 mm et hauteur de1m0492 ± 2 mm.
- Intérieur : longueur moyenne de 1m982 ± 3 mm, largeur de 68,1 cm ± 2 mm et profondeur de 87,4 cm± 2 mm.
sa surface au sol est de 0,98 x 2,28 = √5 = 2,236 m² ± 0,0016. la surface du profil intérieur du coffre qui mesure 1,982 x 0,874 = 1,73226 m² = √3 ± 0,0002
Pourrions-nous trouver ailleurs, dans les dimensions de ce coffre, le nombre suivant de la suite de Fibonacci, à savoir le 8, dont la racine est 2,828 ? En mesurant de la même manière les surfaces des faces extérieure et intérieure de l’objet, nous pouvons constater que la surface au sol (2,236) + la surface intérieure du petit coté du coffre (0,5958) nous donne 2,831 = √8 ± 0,003.
Il est intéressant de noter que le volume intérieur du coffre est de 1,1806 m³, ce qui, converti en coudée nous donne 8,2247 c³. Or, cette valeur est exactement le produit du nombre PI et du nombre PHI².
1,982 x 0,874 x 0,681 = π x Φ en coudée cube ± 0,006. La valeur exacte est comprise dans les marges d’erreur.
Concernant le volume du coffre, nous pouvons également nous apercevoir que le volume extérieur est le double du volume intérieur.
Voir aussi
- La grande pyramide gizeh
- Mesure de la pyramide de Khéops
- encore quelques image de synthèse: http://www.kheops-project.com/galerie/la-chambre-du-roi.html
- où est passé le bloc qui trainait dans la chambre du roi ? => https://pyramidales.blogspot.com/2011/02/pyramide-de-kheops-les-deux-entrees-et.html
- exploration sous la chambre: http://www.gizapyramid.com/aboveking.htm
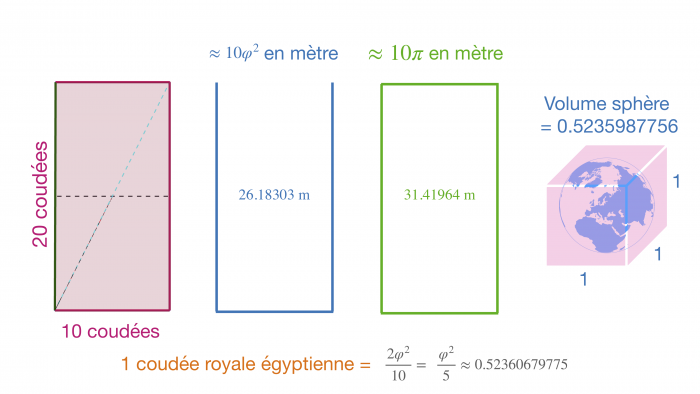
- Coudée royale égyptienne