Mètre

Kilometre definition

Le mètre est une unité de mesure de longueur qui équivaut à un 1/10 millions de la longueur du quart du méridien terrestre qui passe par les pôles.

Voici la chronologie de l'invention du mètre issues des recherches cités sur cette page: https://martouf.ch/2021/03/le-metre-une-matrice-universelle-a-lorigine-mysterieuse/

Wikipedia

Voici l'histoire du mètre inventé lors de la révolution française pour en finir avec les unités en rapport avec la longueur du pied et du coude du roi.... ainsi on défini une mesure universelle liée à la taille de la Terre.

Puis les astronomes, Méchain et Delambre sont envoyés mesurer le méridien de Barcelone à Dunkerque pour établir cette mesure. Ça n'as pas été une mince affaire. Il se trouve même que le mètre provisoire était plus précis que le nouveau ! Le mètre actuel a changé plusieurs fois de définition, mais pas de longueur. Il est 0.2 mm trop court !

Méchain a eu des soucis avec ses mesures à Barcelone. Il se trouve qu'il a fait deux fois des calculs et à trouvé deux valeurs différentes ! Il était effondré, car il n'a pas trouvé l'erreur. Il a même voulu cacher puis brûler ses carnets. Il ne voulait plus rentrer. Sa femmes est allée le chercher à Barcelone.

Il avait découvert des erreurs aussi dans le fondement de la définition. Soit le fait que la figure de la Terre n'est pas celle que l'on croyait et que l'on ne peut pas extrapoler le mètre ainsi avec un méridien si court.

Méchain est retourné à Barcelone pour refaire ses calcul et mesures qui le hantait. Mais il est mort de la malaria là bas. Il n'y jamais fini.

Delambre a repris ses carnets et a masqué l'erreur. La mesure d'un méridien faite en amérique du sud a été utilisée comme nouvelle source de donnée. Le mètre a été proclamé, il est le fruit de cet effort révolutionnaire qui vise à l'universalité.

Les conquêtes passent le mètre reste. Adapdation de ce que Napoléon aurait dit.

https://www.techniques-ingenieur.fr/actualite/articles/mesure-du-1er-metre-une-erreur-qui-changea-le-monde-2715/

Procés-verbaux de la chambre des députés - France. Chambre des députés

La fixation provisoire de la longueur du mètre en 1793 et 18 germinal 3 et révoquée et la version définitive est adoptée le 19 frimaire an 8 (10 décembre 1799). Elle vaut 3 pieds 11 lignes 296/1000 https://books.google.ch/books?id=2TIwAAAAYAAJ&pg=PA536&lpg=PA536&dq=La+fixation+provisoire+de+la+longueur+du+m%C3%A8tre&source=bl&ots=_LjnLfCX_I&sig=N272dDWk2qdraqhydRDWXBs535s&hl=fr&sa=X&ved=2ahUKEwjm693OzdzfAhUQl4sKHfIFBpAQ6AEwA3oECAcQAQ#v=onepage&q=La%20fixation%20provisoire%20de%20la%20longueur%20du%20m%C3%A8tre&f=false

Le problème

Triangle-des-bâtisseurs-origine-coudée-royale-égytienne.png

Fleur-de-vie-origine-coudee-royale-egyptiennen-2048x1816.png

Il se trouve que le mètre a un lien tout à fait précis avec la coudée royale égyptienne déjà utilisée dans l'égypte antique.

Mais aussi avec le pied Drusien mesure 33.3396 cm. Soit ~1/3 de mètre. https://enseignement-latin.hypotheses.org/tag/pied-drusien

Mais encore avec l'empan correspond à 1/5 de mètre.

Définition de la coudée royale

coudée royale égyptienne = π/6 en mètre = (φ²)/5 => 0,523598.... → soit le 1/6ème de la circonférence d'un cercle de 1 mètre de diamètre.
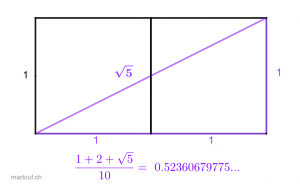
coudée royale égyptienne = (1+2+√5)/10 en mètre => 0,523606... → 1/10 du périmètre du triangle des bâtisseurs en mètre (triangle rectangle dont l'hypoténuse est la diagonale d'un double carré.)

Cette double définition nous rappelle bien la philosophie hermétique, qui présente toujours des polarités. On a ici une définition masculine basée sur un double carré, tout en droites. Et l'on a une définition féminine tout en rondeur déterminée à l'aide d'un cercle. C'est le compas et l'équerre.

Pour en savoir plus => https://martouf.ch/2019/11/quest-ce-que-la-geometrie-sacree-introduction/

Simple coïncidence ?

Occurrences du mètre dans des constructions anciennes

Il se trouve que de nombreuses constructions anciennes ont des mesures en mètres. Notamment des pierres angulaire. Mais aussi des largeur de portes, des murs, etc...

Il y a aussi des objets qui ont des mesures en mètre.

Ça fait beaucoup de coincidences.

Voici une liste: https://martouf.ch/2020/12/liste-de-la-presence-du-metre-avant-son-invention-officielle/

Le disque de Nebra
Stonehenge
le disque de chevroche
Les blocs en H de Puma Punku
L'église de Saint-Nectaire contient une niche de 1 mètre et une pierre de 1 coudée l'un à côté de l'autre
La diagonale des pierres angulaires de la Cathédrale de Fribourg fait 1 mètre
La pierre angulaire de la cathédrale de Laon comporte le mètre
La largeur de la porte gauche de la façade de la cathédrale Notre-Dame de Paris mesure exactement 2,000 m.
La largeur des portes du donjon du Château de Chambord mesure 1,000 m et 90,0 cm
Les deux gravures fichées dans les murs de l’Abbatiale de St- Nectaire du 11ème siècle mesurent 1,00m et 52,4 cm
La grande pierre fichée dans le mur de l’abbatiale de Conques mesure 1,00 m.- EGLISE DE ST DIERY , la porte mesure 100 cm ± 0,1.
La salle du coricancha à Cuzco mesure 10m de long à ± 0.01 et largeur des murs de 1m ± 0,005
La porte du soleil a Tiahuanaco fait 3 mètres de haut et 4 mètres de large
L'Ahu de Tongariki sur l'ile de Pâques fait 100m de long
Les Grottes de Barabar, notamment celle de sudama montrent plein de mesure en mètre
La distance entre le sol et le centre du conduit du mur Nord de la chambre du roi de la pyramide de Khéops fait 1 mètre. Cette chambre a aussi des dimensions qui montrent de manière numérique π et φ pour autant qu'on les mesures en mètre....
La Distance Olympie - Mycène = 100 km
Sur le planétarium de Gizeh: les pyramides sont placées sur les orbites moyenne des planètes à une échelle de 1:100 millionième en mètre !

La page des mesure des bloc H de PumaPunku https://digi.ub.uni-heidelberg.de/diglit/stuebel_uhle1892/0165/image Pour la citation le permalien est: https://digi.ub.uni-heidelberg.de/diglit/stuebel_uhle1892/0165

Le livre en entier.. tiahanacu et pumapuku https://digi.ub.uni-heidelberg.de/diglit/stuebel_uhle1892/0004

L'avis de Quentin Leplat

Quentin Leplat a pas mal creusé la question:

L'avis des zététiciens

Ils réfutent tout.... la taille précise de la coudée et la présence du mètre dans l'antiquité du seul fait que l'histoire du mètre est bien documentée et ne raconte pas ceci... le reste n'est que coincidence....

Quelques sources et références

Rapport de l’Académie des sciences sur le choix d’une unité de mesure, en annexe de la séance du 26 mars 1791

https://www.persee.fr/doc/arcpa_0000-0000_1886_num_24_1_13098_t1_0394_0000_6

Instruction sur les mesures déduites de la grandeur de la Terre : uniformes pour toute la République, et sur les calculs relatifs a leur division décimale https://archive.org/details/instructionsurl00fran/page/12/mode/2up

Les origines du système métrique en France et la Convention du mètre de 1875, qui a ouvert la voie au Système international d'unités et à sa révision de 2018

https://www.sciencedirect.com/science/article/pii/S1631070518301695

Talleyrand et l’établissement du système métrique http://www.talleyrand.org/politique/talleyrand_systeme_metrique.html

Le système métrique des poids et mesures ; son établissement et sa propagation graduelle, avec l'histoire des opérations qui ont servi à déterminer le mètre et le kilogramme

https://archive.org/details/lesystmemtri00bigo/page/n13/mode/2up

Décret proposé par le comité d'agriculture et de commerce sur l'uniformité à établir dans les poids et mesures, lors de la séance du 8 mai 1790

https://www.persee.fr/doc/arcpa_0000-0000_1883_num_15_1_6816_t1_0443_0000_4

Résolution 6 de la 11e CGPM (1960) https://www.bipm.org/fr/CGPM/db/11/6/

Résolution 1 de la 17e CGPM (1983) https://www.bipm.org/fr/CGPM/db/17/1/

Base du système métrique décimal, ou mesure de l’arc du méridien compris entre Dunkerque et Barcelone https://gallica.bnf.fr/ark:/12148/bpt6k110604s.image.f1

Les unités de longueur à la fin du XVIIIe siècle

http://aviatechno.net/unites/pieds.php

Mesures linéaires

https://www.geo-anse.com/geo/Inventaire/l_lineaires.htm

Mesure du 1er mètre : une erreur qui changea le monde

https://www.techniques-ingenieur.fr/actualite/articles/mesure-du-1er-metre-une-erreur-qui-changea-le-monde-2715/

La coudée Égyptienne et le complot métrique

https://irna.fr/La-coudee-Egyptienne-et-le-complot-metrique.html

Le mètre, Pi et Phi selon l’astro-géométrie : un mythe

https://irna.fr/Le-metre-Pi-et-Phi-selon-l-astro-geometrie-un-mythe.html Les contradictions des chercheurs numérologues

https://irna.fr/Les-contradictions-des-chercheurs-numerologues.html

Piste à creuser sur la famille Méchain

La famille Méchain, vien de Laon. La cathédrale de Laon contient une pierre angulaire qui marque le mètre !

Pierre François André Méchain, né à Laon le 16 août 1744 et mort à Castellón de la Plana (Espagne) le 20 septembre 1804. https://fr.wikipedia.org/wiki/Pierre_M%C3%A9chain

Comme l'histoire officielle nous le raconte. Pierre Méchain a eu des soucis de mesure. Il a même voulu faire disparaitre ses carnets.

Il effectue également, avec Jean-Baptiste Delambre, une mesure de l'arc du méridien Dunkerque-Barcelone afin de déterminer précisément le mètre, mais il refuse de communiquer ses mesures à cause d'une anomalie de 3 secondes d'arc qui l'obsède jusqu'à sa mort, au point de la cacher dans ses notes. C'est d'ailleurs pour refaire la mesure qu'il retourne en Espagne, où il meurt de la fièvre jaune, le 20 septembre 18041. C'est son collègue Delambre qui s'est aperçu en 1806 de l'erreur de calcul de Méchain (écart de mesure de 0,229 mm)

Le projet de mesure du méridien avait du plomb dans l'aile.

Fait intéressant, c'est que son propre fils, Jérôme Isaac Méchain, se trouvait à la même époque en égypte, avec la campagne Napoléonienne. ( 19 mai 1798 au 31 août 1801 https://fr.wikipedia.org/wiki/Campagne_d'Égypte)

S'était un des 4 astronomes de la commission des sciences et des arts.

Est-ce que face à cette incertitude des mesures, le mètre ne serait pas revenu d'égypte avec la famille Méchain ?

Jérôme Isaac Méchain, Élève astronome, il est nommé consul général en Orient, puis bibliothécaire adjoint de l'Institut d'Égypte à partir du 8 septembre 1800.

Il quitte prématurément l'Égypte, et fait par la suite une carrière consulaire.

Car que faisaient les scientifiques en égypte ?.... et bien certains, comme Edmée Jomard s'intéressait beaucoup au systèmes de mesure des égyptiens.

(Monge aussi était en égypte... c'était le 1er au sommet de la grande pyramide !)

Voici son livre de Edmée Jomard, "Mémoire sur le système métrique des anciens égyptiens, contenant des recherches sur leurs connoissances géométriques et sur les mesures des autres peuples de l'antiquité" https://digi.ub.uni-heidelberg.de/diglit/jomard1809bd3_1_1/0502/image

Il indique cette citation sur la première page de son livre:

On se convaincra, d'après ces recherches, que les mesures itinéraires, des anciens sont plus exactes qu'on ne le croit. En les comparant au plan de la terre, tel qu'il nous est connu, il est souvent difficile, quelquefois même impossible, de décider si les erreurs que l'on croit apercevoir dans ces itinéraires, doivent être rejetées plutôt sur le compte des anciens que sur l'imperfection de nos connoissances actuelles.
"Recherches sur la géographie systématique et positives des anciens, par M. Gosselin"

Donc les savants de la campagne d'égypte sont conscients que les mesures des anciens ne sont pas moins bonnes que le leurs... Donc potentiellement valables.

"Il est donc naturel de pense que l'étude des monnumens laissés par les Égyptiens y fera retrouver leur système métrique: c'est là la fin essentielle de notre travail, notre but n'étant pas de donner un tableau de toutes les mesures appartenant aux divers peuples et cités par les auteurs. Outre que cette recherche serait hors du plan de l'ouvrage et au-dessus de nos forces, elle se trouvera faite en partie, pour ainsi dire, par la seule détermination des mesures égyptiennes. Celles-ci, en effet ont donné naissance à beaucoup d'autres, telles, par exemple, les mesures hébraïque, ainsi que l'atteste positivement S. Épiphane. "
Description de l'Egypte ou Recueil des observations et des recherches qui ont été faites en Egypte pendant l'expédition de l'armée française. Tome 7: https://gallica.bnf.fr/ark:/12148/bpt6k28004p/f10.image#

Bon, la définition du mètre est antérieure.... là aussi il faudrait savoir d'où elle vient.

Histoire du mètre au 17ème siècle

Si la présence du mètre en des temps reculé est controversée. Elle ne l'est pas au 17ème siècle. L'idée du mètre n'est pas sortie d'un chapeau à la révolution française.

La plus ancienne définition est celle de l'Abbé Mouton:

Vers 1670, Gabriel Mouton, vicaire de l'église Saint-Paul à Lyon, après avoir montré, par les trop nombreux exemples que présente le passé, combien il est difficile de conserver aux mesures une longueur invariable, certaines dépendaient de la longueur du pied du roi, il propose un ensemble de mesures linéaires, dites par lui géométriques, qu'il assujettit à la division décimale.

Autrement dit, il propose l'utilisation de la base 10 alors qu'à l'époque on passait d'une unité à son multiple ou sous multiple en multipliant ou divisant le plus souvent par 6 ou 12. (base 6, base 12)

Il appelle alors milliare, centuria, decuria, virga, virgula decima, virgula centesima, virgula millesima.

L’appellation virga pourrait provenir de verge, tige de balancier car Mouton pensait retrouver cette longueur en tout point du globe, avec un pendule battant la même période.

Le milliare ou mille serait la longueur de l'arc de 1' (une minute) de grand cercle de la Terre(méridien), de sorte que la virga et la virgula (1/1 000 ou 1/10 000 du mille géométrique) auraient répondu à la toise et au pied.

Gabriel Mouton est donc le premier physicien à proposer la définition d'un étalon universel de longueur basé sur la dimension du globe terrestre : la virgula geometrica, définie comme la six-cent-millième partie d'un degré d'un arc de méridien.

Avec les données actuelles la virgula = 111,111 km / 600 000 = 0,18 m

Et la virga = 1,80 m n’était pas très loin de la toise.

On voit que le projet de Mouton correspond, dans le principe, à celui qui a été réalisé, plus de 120 années plus tard, par notre système métrique.

https://fr.wikipedia.org/wiki/Gabriel_Mouton

Et c'est fou le nombre de savants liés à l'histoire de la métrologie et notamment de la définition et la mesure du mètre utilisé actuellement qui sont allés en égypte ! ... et on nous le dit jamais dans les manuels scolaires !

Pour moi le cas le plus emblématique est Edmée Jomard. Il dit dans son Mémoire sur le système métrique des anciens égyptiens… :

" Mais le périmètre de la grande pyramide de Memphis avoit 30 secondes du degré propre à l’Egypte, autrement cinq stades compris chacun 600 fois dans ce même degré: l’apothème avoit un stade; le côté, 500" .

La longueur du degré du méridien propre à l’égypte (30° de latitude) mesure 110852.4248 m. Si on divise cette longueur par 120 on obtient 923.8m pour le périmètre de la pyramide, soit 230.942 m pour un côté.

=> Calculateur de de degré de méridien: https://martouf.ch/outils/calculateur-longueur-degre-meridien-terre.html

Ce qui à une coudée près correspond aux 440 coudées officiellement admises. (mais avec de grandes variations suivants les auteurs !) La différence s’explique probablement à savoir si l’on prend en compte le socle de la pyramide où non !

Donc il cherche là un lien entre la taille de la grande pyramide et la mesure de la Terre.

Jomard n'est pas le premier. Un Certain Newton s'y est beaucoup intéressé aussi, ceci afin de vérifier sa théorie de la gravitation !

Newton cherche une mesure de la Terre dans la grande pyramide de Gizeh

Newton veut faire valider sa théorie de la gravité en se basant sur les mesure de la grande pyramide.

Le physicien (et alchimiste) Newton avait besoin d'une mesure précise de la Terre pour affiner sa théorie de la gravité. Il pensait pouvoir retrouver la taille d'un degré de méridien en fonction d'une mesure ancienne égyptienne encodée dans la dimension de la grande pyramide de Giezh. (voir aussi sa dissertation sur le unités de mesure anciennes)

Il a voulu utiliser les mesures de l'astronome anglais John Greaves, un passionné d'unités de mesure antiques qui a visité la pyramide en 1638. https://fr.wikipedia.org/wiki/John_Greaves_(astronome)

Mais ça ne semblait pas suffire. Newton a aussi compté sur les mesure du savant italien Burattini, qui a vécu en égypte entre 1637 et 1641 et y a mesuré la pyramide.

Tito (Livio) Burattini vécut de 1637 à 1641 en Égypte où il prépara une triangulation cartographique du pays, mesura de nombreuses pyramides, obélisques et monuments et essaya de les classifier.

En 1675 paraît son ouvrage Misura Universale, dans lequel il renomme l'unité de mesure universelle proposée par John Wilkins en mètre (metro cattolico, traduction acceptable, dans le contexte socio-religieux de l'époque, de mesure universelle) et la redéfinit comme étant la longueur d'un pendule qui oscille avec une demi-période d'une seconde, soit une longueur correspondant à environ 993,9 mm actuels. Méconnue à l'époque de Burattini, la gravitation fait cependant que cette valeur puisse varier selon le lieu. Il faudra néanmoins attendre plus d'un siècle pour qu'en 1791 l'Académie des sciences redéfinisse cette unité pour lui donner une valeur plus constante.

Misura Universale, où est établie une mesure universelle de longueur: le mètre, défini comme la longueur d'un pendule qui oscille avec une demi-période d'une seconde. https://fr.wikipedia.org/wiki/Tito_Livio_Burattini

https://holistique.wordpress.com/2008/01/29/le-pendule-le-metre-et-la-seconde/

En 1675, Burattini publie Misura Universale, ouvrage dans lequel il renomme la mesure universelle de Wilkins en mètre universel « metro cattolico » (qui signifie "mesure universelle") et la redéfinit comme étant la longueur d'un pendule qui oscille avec une demi-période d'une seconde, soit environ 993,9 mm actuels.

Pendulum2secondclock

Il imagine ainsi un système d’écriture fondé non sur un alphabet mais sur un système idéographique compréhensible internationalement. Il travaille six ans à ce projet qu’il présente dans An Essay towards a Real Character and a Philosophical Language. Dans cet ouvrage, Wilkins propose également l'adoption d'une mesure universelle (universal measure), d'unités décimales, basée sur le principe d'un pendule battant une seconde, et dont la longueur fondamentale est de 38 pouces prusses (1 prussian inch = 26,15 mm), soit de 993,7 mm. https://fr.wikipedia.org/wiki/John_Wilkins

Le savant Italien Tito Livio Burattini redéfinira quelques années plus tard cette unité et la renommera le mètre (metro cattolico).

(au passage, la théorie de la gravité n'était pas connue... vu que Newton ne l'avait pas finalisée... mais le mouvement du pendule dépend de la gravité et donc de la latitude du lieu.... et là je t'invite à voir ce qu'il se passe si tu te places au pôle.... avec quelle valeur, on va dire... emblématique.... on simplifie la formule ... et ce que ça peut signifier comme définition du mètre ! A mon avis on avait là la véritable valeur du mètre, le st-graal de générations de chercheurs.. un mètre en lien avec la terre et avec la géométrie sacrée. ... et on découvre que notre version du mètre est fausse... que la version provisoire était plus juste que la version définitive.... Je ferai un article là dessus un jour... mais d'abord je vais te laisser chercher... :p )

Mais finalement Newton a utilisé les travaux de Jean Picard qui a mesuré en 1669-1671 un degré de méridien. Et du coup on a eu pour la première fois depuis Eratosthène une mesure de la circonférence de la Terre un peu plus juste.

https://fr.wikipedia.org/wiki/M%C3%A9ridienne_(g%C3%A9od%C3%A9sie)#La_m%C3%A9ridienne_de_Picard https://gallica.bnf.fr/ark:/12148/btv1b7300361b.image

Dommage que Newton ne connaissait pas les renfoncements des 8 faces de la grande pyramide... c'est justement ce qui montre le taux d'aplatissement de l'éllipsoïde qu'est la Terre.. et ce que Newton cherchait... (une idée.... au passage... à vérifier pour toi qui aime les énigmes... 😉 )

Expédition géodésique française

Voyage aller et retour de La Condamine 1735 1744

Au cours du XVIIIe siècle, l'Académie des sciences organisa plusieurs expéditions scientifiques, outre-mers, afin de pouvoir répondre à un certain nombre de questions scientifiques, notamment sur la forme exacte de la Terre (était-elle parfaitement sphérique, aplatie aux pôles ou aplatie à l'équateur ?).

La Condamine, par son sens de l'organisation et des contacts humains, sauve du désastre l'expédition française qui, après bien des péripéties, obtient la mesure de trois degrés du méridien de Quito. On pensa longtemps que les résultats produits par les instruments et les conditions de mesure de l'époque restaient chargés d’incertitudes, mais « Plus de deux cents ans plus tard, les géodésiens constateraient que leurs mesures étaient d’une étonnante exactitude, largement supérieure à celles que Maupertuis avait effectuées en Laponie. »

C’est au cours de ce long périple que La Condamine aura aussi « l’idée d’utiliser la “longueur d’un pendule à secondes à l’équateur, à l’altitude de Quito” comme “mesure naturelle” […] définie par l’attraction gravitationnelle de la Terre plutôt que d’une mesure arbitraire comme le pied d’un roi qui fournirait un instrument normalisé à l’usage de toutes les nations ». Il anticipe ainsi sur ce qui, cinquante an plus tard, allait inspirer aux savants français l’invention du mètre.

https://fr.wikipedia.org/wiki/Charles_Marie_de_La_Condamine

basée sur: Robert Whitaker, La femme du cartographe, (The Mapmaker’s Wife, a True Tale of Love, Murder, and Survival in the Amazon, 2004), traduit par Odile Demange, Payot & Rivages, 2018

Malgré les nombreuses tribulations de cette expédition, les résultats rapportés produisaient des effets à court, moyen et long terme. Le résultat le plus immédiat en fut évidemment la valeur du degré d'arc de méridien proche de l'équateur. Dans son compte-rendu à l'Académie royale des sciences du 14 novembre 1744 (donc sept ans après celui de Maupertuis), Bouguer attribuait au degré à la latitude moyenne de la chaîne une valeur de 56 753 toises, après réduction au niveau de la mer et à la température d'étalonnage de sa toise. La Condamine avait obtenu 56 749 toises. Ce résultat, il est vrai, ne fit que confirmer ce que l'on savait depuis le retour de l'expédition de Laponie, à savoir que la figure de la Terre correspondait à un sphéroïde aplati vers les pôles.

https://fr.wikipedia.org/wiki/Exp%C3%A9ditions_g%C3%A9od%C3%A9siques_fran%C3%A7aises

Dit dans: https://www.youtube.com/watch?v=aByCkU80o0w&t=878s

La figure de la Terre n'est pas un élipsoïde de révolution. Donc ça remet en cause la mission. Si chaque méridien a une longueur propre, alors on ne peut pas extrapoler un méridien en mesurant juste un bout ! Il a donc fallu reprendre la mesure du méridien du pérou/équateur mesuré 60 ans plus tôt par La Condamine 1735 1744. https://fr.wikipedia.org/wiki/Exp%C3%A9ditions_g%C3%A9od%C3%A9siques_fran%C3%A7aises https://fr.wikipedia.org/wiki/Charles_Marie_de_La_Condamine

Lacaille et la méridienne du Cap

Envoyé en 1751 au cap de Bonne-Espérance pour faire un catalogue d'étoiles australes et observer la parallaxe de la Lune, l'abbé Nicolas-Louis de Lacaille complétait ses travaux par l'observation d'un arc de méridien auquel il attribuait la valeur de 57 037 toises par degré à la latitude (sud) de 33° 18′. Il mesurait aussi la longueur du pendule simple battant la seconde. L'impact de ces expéditions sur les connaissances scientifiques du milieu du XVIIIe siècle peut être comparé à celui de l'exploration spatiale sur les connaissances scientifiques de la fin du XXe siècle.

Lacaille et le mètre provisoire

Le mètre provisoire de 1740 de l'abbé Louis Lacaille, plus long de 0,095 mm que le mètre réel, est remplacé en 1799, après 6 ans, par le "mètre vrai" de Delambre et Méchain qui est plus court de 0,23 mm que le mètre réel.

https://fr.wikipedia.org/wiki/Nicolas-Louis_de_Lacaille

Il effectue une longue mission dans l'hémisphère austral, d'octobre 1750 à juin 1754, où il est envoyé pour mesurer l'arc du méridien.

L'Académie retient, sans le savoir, une grandeur étalon deux fois plus éloignée de la vérité que ne l'était la valeur provisoire retenue en 1793. Le "mètre vrai" de Delambre et Méchain devient en 1799 "la référence", l'étalon principal du système métrique.

C'est encore la valeur la plus fausse qui est confirmée pour la France en 1872 et pour le commerce international en 1903, c'est à dire "le mètre vrai" de Delambre et Méchain trop court de 0,23 mm..

Il en résulte, que sur la base de la grandeur du mètre international, la plus récente mesure de la longueur du méridien est de 40007,864 km

http://www.mesures.org/

Mesure de la Terre à des périodes anciennes

Au delà de la mesure du mètre, c'est reconnaitre que les anciens savaient mesurer la Terre. Donc voilà un historique des mesure de la Terre.

http://www.mesures.org/MesureursDeTerre.htm

Saint Epiphane (438-496), évêque de Pavie.
D'après F. Jedrzejewski (p.63) " le chemin sabatique" des Hébreux évalué par St Epiphane
Est de 2000 coudées de 0,56 m et vaut 6 stades grecs de 186,6 m = 600 x 0,3111 m
Conclusion le méridien est de 0,3111 x 600 x 10 x 60 x 360 = 40 318 km

L'abbé Moreux

L'abbé Moreux a écrit tout un livre qui s'appelle la Science mystérieuse des pharaons.

https://archive.org/details/collection_complete_POUR_COMPRENDRE_ABBE_THEOPHILE_MOREUX_et_autres_auteurs/La%20science%20myst%C3%A9rieuse%20des%20pharaons%20%281943%2C%20Abb%C3%A9%20Th.%20Moreux%29/page/38/mode/2up

A la p.40 commence le chapitre dédié à l'astronomie.

Dès qu’on eut acquis la conviction que la Terre ressemblait à une boule lancée dans l’espace, comme Mars, la Lune ou Jupiter, il vint à l’idée des savants de mesurer une portion du Globe pour en déduire sa grosseur réelle. Un méridien est un grand cercle passant par les pôles : il contient donc 360 degrés. Or, si nous avions la valeur de un degré, une simple multiplication nous dirait la longueur de la circonférence entière. Mais alors, comment savoir qu’on a parcouru un degré en allant du Nord au Sud ? Ici, l’astronome intervient : toutes les fois que nous montons vers le Nord, un examen, même superficiel, de la voûte céleste indique à l’observateur que son pôle monte dans le ciel.

Dans les régions septentrionales, l’étoile polaire est presque au-dessus de nos têtes, et, tout compte fait, le pôle céleste monte de un degré dans le ciel lorsque nous avons parcouru un degré sur la Terre.

Tel est le principe de la méthode. Les applica tions ne furent cependant pas sans difficultés. Quelle était la marche à suivre pour mesurer un degré ?

Au xvie siècle, un médecin nommé Fernel, s’était amusé à compter le nombre de tours qu’avaient fait les roues de sa voiture en allant de Paris à Amiens. Le procédé était au moins ingénieux, mais il ne pouvait être susceptible d’une grande précision ; et cependant Fernel était arrivé ainsi à établir, pour la valeur du degré, 57 070 toises ou 111 532 m. 43, et ce n’était déjà pas si mal, ainsi que nous allons le voir.

(...)

Nous venons de voir qu’en fait, notre mètre reste encore une unité de pure conven tion fondée sur un principe manifestement faux. Puisque tous les méridiens diffèrent entre eux, il est bien évident qu’une unité de longueur ne peut êtie basée sur leur grandeur variable elle-même.

Il y aurait eu un moyen de mettre tout le monde d’accord ; mais personne n’y a songé et ce moyen le voici : prendre comme grandeur linéaire l’axe terrestre lui-même, ce fameux rayon polaire qui, lui, est invariable, tout au moins pendant des millions d’années. 11 est vrai qu’au temps de la Révo lution, nul savant n’était à môme de déterminer la valeur du rayon polaire de notre globe, constante qui dépend de l’aplatissement du sphéroïde terrestre.

(...)

Conclusion : à l’heure actuelle nous pourrions posséder une unité de longueur précise et inva riable, basée sur la valeur du rayon polaire.

Eh bien, cette unité, nous la trouvons à la base même de la construction de la Grande Pyramide et nous allons voir comment.

Les Egyptiens comptaient les longueurs en pouces et en coudées, mais il y avait deux systèmes de mesure ; les mesures ordinaires pour le peuple et les mesures sacrées, employées seulement par les prêtres. C’est la coudée sacrée qui a servi aux cons tructeurs de la Pyramide de Khéops ; on la dé signe souvent aussi sous le nom de coudée pyramidale et l’on sait qu’elle était divisée elle-même en 25 pouces pyramidaux.

Or, chose étrange, le pouce pyramidal était très voisin du pouce anglais, puisqu’il faut 999 pouces pyramidaux pour faire 1 000 pouces anglais. Ceci nous donne pour le pouce pyramidal : 25 mm. 4 264 et pour la coudée pyramidale ou sacrée :

25,4264 x 25 = 0m. 635660.

La coudée sacrée qui a servi aux architectes égyptiens dans la construction de la Grande Pyra raide valait donc 635mm,660.

Multipliez maintenant cette coudée par 10 mil lions et vous trouverez 6.356.600 mètres : c’est pré cisément la valeur que notre science actuelle assigne à la longueur du rayon polaire de la Terre ; le nombre des kilomètres est exact ; l’écart no porte que sur le chiffre suivant 6 au lieu de 7, mais nos mesures actuelles comportent encore une incerti tude du même ordre de grandeur.

Ainsi, la coudée sacrée représenterait la dix- millionième partie du rayon polaire de la Terre et cela avec une valeur exacte à un centième de millimètre près !

(p.48)

Le mètre dans la pyramide de Khéops

La pyramide de Khéops comporte plusieurs endroits qui montrent que le mètre pourrait bien être connu ou indirectement connu des bâtisseurs.

C'est notamment les dimensions de la chambre de Khéops qui nous le montre.

le canal à côté de l'entrée de la chambre a son centre (qu'on trouve en faisant une croix entre les angles du carré) exactement à 5 coudées royales égyptienne du bord du mur Est. Mais également exactement à 1m (à 5mm près) de hauteur par rapport au sol.
le sol de la chambre de Khéops peut être coupé en deux triangles égaux, de 5.235m pour le petit côté de 10,47m pour le grand et donc d'une hypoténuse de 11,7m. Ce triangle a donc une surface de 27,4 m^2 et un périmètre de 27,4 m !!! Identique ! .. mais uniquement si on s'exprime en mètre! (on retrouve ici une forme du fameux nombre 273) qui correspond à la proportion π/4.)
Si l'on utilise la longueur du côté de la base de la pyramide de Khéops (440 coudées royales ~= 230m) pour réaliser un rectangle d'or, on peut créer le cercle circonscrit de ce rectangle. La circonférence de ce cercle fait 1,618 Km. Soit le nombre d'or en km. Ce résultat "numérologique" n'est possible uniquement si on utilise le mètre.

voir aussi