Différences entre versions de « Coudée royale égyptienne »
(liste de valeurs de coudées) |
(karnak) |
||
| (5 versions intermédiaires par le même utilisateur non affichées) | |||
| Ligne 68 : | Ligne 68 : | ||
* la paume = le long côté + le petit côté - hypoténuse | * la paume = le long côté + le petit côté - hypoténuse | ||
| − | On retrouve ici aussi le principe de la suite de | + | On retrouve ici aussi le principe de la [[suite de Fibonacci]]. |
| − | Ces unités sont reliées entre elles par un facteur du nombre d'or. Ce qui permet de les retrouver par la suite de | + | Ces unités sont reliées entre elles par un facteur du nombre d'or. Ce qui permet de les retrouver par la suite de Fibonacci: |
* 1 paume + 1 palme = 1 empan | * 1 paume + 1 palme = 1 empan | ||
* 1 palme + 1 empan = 1 pied | * 1 palme + 1 empan = 1 pied | ||
| Ligne 78 : | Ligne 78 : | ||
<youtube>https://www.youtube.com/watch?v=0wkqocwcc-Q</youtube> | <youtube>https://www.youtube.com/watch?v=0wkqocwcc-Q</youtube> | ||
| + | |||
| + | |||
| + | Avec ce système de mesures, on obtient une cohérence stupéfiante des unités de mesures. On a là aussi un moyen numérologique d'exprimer des constantes mathématiques si on les exprimes en mètre ! (de la même manière que dans la [[chambre de Khéops]]... ) | ||
| + | |||
| + | * 5 empans de 20cm donnent 1 mètre. | ||
| + | * 5 pieds de 32,36 cm, soit le périmètre du pentagone inscrit dans le cercle, donnent 1,618 m le [[Nombre d'or|Nombre d'Or]] en [[mètre]]. | ||
| + | * 5 coudées de 52,36 cm donnent 2,618 m soit le carré du Nombre d'Or en mètre. | ||
| + | * 6 coudées de 52,36 cm donnent 3,1416 m soit la constante [[Pi]] exprimée en mètre. | ||
| + | * 6 pieds de 32,36 cm valent 1 toise, soit 1,9416 mètre soit le rapport des deux constantes Pi et Phi. π/φ = 1,9416 | ||
== Observations == | == Observations == | ||
| Ligne 91 : | Ligne 100 : | ||
ou encore vus sous un autre angle: | ou encore vus sous un autre angle: | ||
[https://www.google.com/search?sxsrf=ALeKk01zAnmUS_o4NctM2VeaPGKxd9cNDA%3A1614714236808&source=hp&ei=fJU-YMS2LoyZkwWph46gDA&iflsig=AINFCbYAAAAAYD6jjN3t_aCxjFUUZqYpUEXgC3z3ZZzL&q=%CF%80-%CF%86+%2B+1&oq=%CF%80-%CF%86+%2B+1&gs_lcp=Cgdnd3Mtd2l6EAMyBggAEBYQHjIGCAAQFhAeOgIIADoICAAQxwEQrwE6AgguOgQIABATOgQIABAeOgYIABAeEBM6BggAEAgQHjoGCAAQBxAeOgYIABAFEB46CAgAEAgQChAeOggIABAWEAoQHlC9CFiFvgFgs8gBaANwAHgDgAH8BYgBySySAQ4xLjEwLjAuMS4yLjQuMZgBAKABAaABAqoBB2d3cy13aXo&sclient=gws-wiz&ved=0ahUKEwjE5Pujr5LvAhWMzKQKHamDA8QQ4dUDCAY&uact=5 π-φ + 1 = 2,52355866484].. ≈ la coudée royale | [https://www.google.com/search?sxsrf=ALeKk01zAnmUS_o4NctM2VeaPGKxd9cNDA%3A1614714236808&source=hp&ei=fJU-YMS2LoyZkwWph46gDA&iflsig=AINFCbYAAAAAYD6jjN3t_aCxjFUUZqYpUEXgC3z3ZZzL&q=%CF%80-%CF%86+%2B+1&oq=%CF%80-%CF%86+%2B+1&gs_lcp=Cgdnd3Mtd2l6EAMyBggAEBYQHjIGCAAQFhAeOgIIADoICAAQxwEQrwE6AgguOgQIABATOgQIABAeOgYIABAeEBM6BggAEAgQHjoGCAAQBxAeOgYIABAFEB46CAgAEAgQChAeOggIABAWEAoQHlC9CFiFvgFgs8gBaANwAHgDgAH8BYgBySySAQ4xLjEwLjAuMS4yLjQuMZgBAKABAaABAqoBB2d3cy13aXo&sclient=gws-wiz&ved=0ahUKEwjE5Pujr5LvAhWMzKQKHamDA8QQ4dUDCAY&uact=5 π-φ + 1 = 2,52355866484].. ≈ la coudée royale | ||
| + | |||
| + | |||
| + | 666 mètres font 1272 coudées | ||
| Ligne 143 : | Ligne 155 : | ||
* 52,39 cm : Newton, Dissertation upon the Sacred Cubit of the Jews. | * 52,39 cm : Newton, Dissertation upon the Sacred Cubit of the Jews. | ||
* 52,37 cm : H. Carter, JEA 3 (1916): 150; Petrie, Pyramids and Temples, 181. | * 52,37 cm : H. Carter, JEA 3 (1916): 150; Petrie, Pyramids and Temples, 181. | ||
| − | |||
* 52,4 cm : J. J. Champollion-Figeac (1824, pp. 289–329) gave a value of 52.4 cm for the royal cubit in “Observations sur les coudées égyptiennes découvertes dans les mines de Memphis.” | * 52,4 cm : J. J. Champollion-Figeac (1824, pp. 289–329) gave a value of 52.4 cm for the royal cubit in “Observations sur les coudées égyptiennes découvertes dans les mines de Memphis.” | ||
| − | |||
* 52,3 cm : Armando Mei, Université de Naples : utilise la valeur 52,3 cm dans ses publications. (2018) | * 52,3 cm : Armando Mei, Université de Naples : utilise la valeur 52,3 cm dans ses publications. (2018) | ||
* 52,3 cm : Nora E. Scott, “Egyptian Cubit Rods”, Department of Egyptian Art, The Metropolitan Museum of Art Bulletin 2016, p. 1, | * 52,3 cm : Nora E. Scott, “Egyptian Cubit Rods”, Department of Egyptian Art, The Metropolitan Museum of Art Bulletin 2016, p. 1, | ||
| Ligne 154 : | Ligne 164 : | ||
* 52,5 cm
: Budge, E.A.W., (1960). An Egyptian Hieroglyphic Dictionary, with an Index of English
Words, King List and Geographical List with Indexes, List of Hieroglyphic Characters, Coptic and Semitic Alphabets, etc. Vol. I. A-Kha, Frederick Ungar Publishing Co., New York. | * 52,5 cm
: Budge, E.A.W., (1960). An Egyptian Hieroglyphic Dictionary, with an Index of English
Words, King List and Geographical List with Indexes, List of Hieroglyphic Characters, Coptic and Semitic Alphabets, etc. Vol. I. A-Kha, Frederick Ungar Publishing Co., New York. | ||
* 52,5 cm : Lepsius Die Längenmaße der Alten, (1884) | * 52,5 cm : Lepsius Die Längenmaße der Alten, (1884) | ||
| − | * 52,5 cm : Carlotti , (1995), ‘Quelques réflexions sur les unités de mesure utilisées en architecture pharaonique’, Les Cahiers de Karnak 10, pp. 127-140 | + | * 52,5 cm : Carlotti , (1995), ‘Quelques réflexions sur les unités de mesure utilisées en architecture pharaonique’, Les Cahiers de [[Karnak]] 10, pp. 127-140 |
* 52,37 cm, John Legon, qui s’appuie sur les travaux de Petrie pour comprendre l’implantation du complexe de Gizeh. | * 52,37 cm, John Legon, qui s’appuie sur les travaux de Petrie pour comprendre l’implantation du complexe de Gizeh. | ||
| − | * 52,35 cm, Manu Seyfzadeh (DOI : 10.4236/ad.2018.62008 ), qui s’appuie sur la publication de Glen Dasch qui déduit de la grande pyramide une coudée dont la variation est comprise entre 52,30 cm et 52,38 cm. Dash, G. (2012). New Angles on the Great Pyramid. | + | * 52,35 cm, Manu Seyfzadeh (DOI : 10.4236/ad.2018.62008 ), qui s’appuie sur la publication de Glen Dasch qui déduit de la grande pyramide une coudée dont la variation est comprise entre 52,30 cm et 52,38 cm. Dash, G. (2012). New Angles on the Great Pyramid.AERAGRAM, 13 , 10-19) |
| − | |||
* 52,35 cm : Mark H. Stone, The Cubit, a history of measurement commentary. (Noté que cet auteur écrit que Dieter Arnold accorde à la coudée royale la valeur de 52,3 à 52,4 cm. page 3) | * 52,35 cm : Mark H. Stone, The Cubit, a history of measurement commentary. (Noté que cet auteur écrit que Dieter Arnold accorde à la coudée royale la valeur de 52,3 à 52,4 cm. page 3) | ||
| Ligne 170 : | Ligne 179 : | ||
* [[Coudée royale égyptienne]] | * [[Coudée royale égyptienne]] | ||
* [[mètre]] | * [[mètre]] | ||
| + | * [[Coudée de Nippur]] | ||
* [[Liste d'unités de mesure]] | * [[Liste d'unités de mesure]] | ||
* [[Mesure des portes de monuments|Mesure des portes]] | * [[Mesure des portes de monuments|Mesure des portes]] | ||
Version actuelle datée du 27 novembre 2023 à 23:14
La coudées royale égyptienne est une unité de mesure ancienne qui vaut 52,36 cm.
Elle a été utilisée pour la construction de la grande pyramide de Gizeh. On la retrouve également plus tard dans la construction des cathédrales, intégrée dans le système de la quine des bâtisseurs. (coudée, pied, empan, palme, paume)
Voir ce qu'on en dit sur wikipedia... (avec des guerres d'écriture):
https://fr.wikipedia.org/wiki/Coud%C3%A9e_royale_%C3%A9gyptienne
Définition
La définition de la coudée est encore sujette à discussion. Les zététiciens y voient une large variance de quelques centimètres. Alors que les archéologues depuis longtemps déterminent cette coudée avec précision.
La définition est géométrique. Mais là il y a deux écoles.
- coudée royale égyptienne = π/6 en mètre = (φ2)/5 => 0,523598.... → soit le 1/6ème de la circonférence d'un cercle de 1 mètre de diamètre.
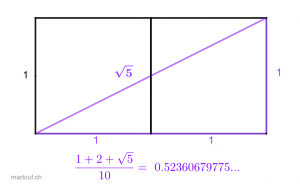
- coudée royale égyptienne = (1+2+√5)/10 en mètre => 0,523606... → 1/10 du périmètre du triangle de l'équerre des bâtisseurs en mètre (triangle rectangle dont l'hypoténuse est la diagonale d'un double carré.)
Cette double définition nous rappelle bien la philosophie hermétique, qui présente toujours des polarités. On a ici une définition masculine basée sur un double carré, tout en droites. Et l'on a une définition féminine tout en rondeur déterminée à l'aide d'un cercle. C'est le compas et l'équerre.
Volume de la sphère
Le volume d'une sphère inscrite dans une cube de 1 de côté vaut 0.52359877... fois le volume du cube.
Soit: (4/3) * π * rayon^3 = 4/3 * π * (1/2)^3 = 0.523598775598... = π/6
En image:
- https://www.pinterest.ch/pin/81768549474121498/
- https://brucelyonsblog.wordpress.com/2010/04/10/unknown-squared-circle-more-than-meets-the-eye-p7/
Mesure
L'architecte Gilles Dormion a mesuré les dimensions de la pyramide de Khéops et notamment la chambre du roi.
Grâce à la géométrie particulière de cette chambre à base d'un double carré, il est possible de déterminer la dimension de la coudée royale égyptienne.
La chambre est en syènite (un sorte de granite sans quartz), une pierre très solide qui s'use très peu et ces pierres sont protégées au coeur de la pyramide.
Gilles Dormion a mesuré 10,47 mètres de long pour cette chambre de 20 coudées de long. Il en déduit donc une coudée royale de 0.5235 mètre.
(A vérifier, il y a un passage de livre qui dit qu'il a repris les valeurs de Dorner pour les mesures qu'il a indiquées sur ses plan de 1996. Est-ce que Dormion a vraiment fait des mesures ?)
Equerre des bâtisseurs
L'équerre des bâtisseurs est un outil pratique qui permet, avec un simple triangle issus d'un double carré de déterminer toutes les mesures de la quine des bâtisseurs.
C'est l'avantage du nombre d'or. C'est que les multiplications et divisions se remplacent par des additions et soustractions ! C'est l'avantage de ce nombre qui est en même temps une suite géométrique et une suite arithmétique !! (on le voit bien avec la suite de fibonacci)
(On retrouve le même genre de raisonnement sur les règles à calcul qui utilisent la propriété des puissances pour remplacer des multiplications par des additions)
La taille de l'équerre est calibrée sur l'empan, soit la longueur entre le pouce et l'auriculaire écarté. Cette mesure semble normalisée à 20cm.
Donc on se retrouve avec un triangle de 1 empan (20cm) pour le long côté et un demi empan (10cm) pour le côté court. Du coup la diagonale du double carré, soit l'hypoténuse du triangle vaut √5 fois le petit côté. (22,360679775... cm)
En combinant ces longueurs on peut générer toutes les autres unités de mesure de la quines des bâtisseurs.
- La coudée = le périmètre du triangle de l'équerre
- Le pied = le petit côté + l'hypoténuse
- L'empan = le long côté
- La palme = hypoténuse + le petit côté - le long côté
- la paume = le long côté + le petit côté - hypoténuse
On retrouve ici aussi le principe de la suite de Fibonacci.
Ces unités sont reliées entre elles par un facteur du nombre d'or. Ce qui permet de les retrouver par la suite de Fibonacci:
- 1 paume + 1 palme = 1 empan
- 1 palme + 1 empan = 1 pied
- 1 empan + 1 pied = 1 coudée
J'explique l'équerre ici en vidéo:
Avec ce système de mesures, on obtient une cohérence stupéfiante des unités de mesures. On a là aussi un moyen numérologique d'exprimer des constantes mathématiques si on les exprimes en mètre ! (de la même manière que dans la chambre de Khéops... )
- 5 empans de 20cm donnent 1 mètre.
- 5 pieds de 32,36 cm, soit le périmètre du pentagone inscrit dans le cercle, donnent 1,618 m le Nombre d'Or en mètre.
- 5 coudées de 52,36 cm donnent 2,618 m soit le carré du Nombre d'Or en mètre.
- 6 coudées de 52,36 cm donnent 3,1416 m soit la constante Pi exprimée en mètre.
- 6 pieds de 32,36 cm valent 1 toise, soit 1,9416 mètre soit le rapport des deux constantes Pi et Phi. π/φ = 1,9416
Observations
π - φ = 1.52355866484...
Donc:
Coudée ≈ π - φ^2
=> voir: https://youtu.be/JswiB6d87cU?t=4770
5 coudées ≈ π et 6 coudées ≈ phi
ou encore vus sous un autre angle: π-φ + 1 = 2,52355866484.. ≈ la coudée royale
666 mètres font 1272 coudées
Le pape sixte V avait tout compris...
http://egypte.chez.com/coudee.html
(366/360)(φ/π) = 0.5150362148
La distance entre le soleil et la Terre est souvent indiquée étant la base d'une Unité Astronomique: l'UA. https://fr.wikipedia.org/wiki/Unit%C3%A9_astronomique 149 597 870 700 mètres.
La distance de la Terre à Mars varie beaucoup au cours du temps. Voici un simulateur pour bien comprendre. => https://www.geogebra.org/m/sya5amCr Cependant on peut aussi comparer la distance moyenne de la Terre à Mars comme étant la distance moyenne de mars au soleil, moins la distance de la Terre au soleil, (soit une UA).
Donc au plus loin (aphélie), mars est à 249 230 000 km (1,666 02 UA) du soleil et au plus près (périhélie) 206 655 000 km (1,381 4 UA). La moyenne entre ces deux valeurs nous donne: 1,52371 UA, soit une valeur qui rappelle fortement les 0,5236 de la coudée. Coïncidence ou pas ?
Par un raccourci on peut donc dire qu'à l'échelle du système solaire on retrouve la même proportion mètre coudée royale. Unité astronomique et orbite moyenne de mars. Ceci est expliqué en image chez Quentin Leplat.
Djed-efrê
Si l'on divise la distance du pôle nord jusqu'à la pyramide de Djedefrê, par le diamètre de la Terre, on trouve l'expression de la coudée royale...
6678282,8 mètres / (2*6378,137) = 523.529268813
J'utilise 2 fois le rayon équatorial pour trouver le diamètre.
Des statistiques pour prouver la valeur de la coudées
il y a 1 chance sur 2901 de trouver un étalon qui soit en rapport en même temps avec π et phi... avec une précision de 99.99% => 0.5236 mètre Si on considère que à partir d'une chance sur 20 c'est significatif et 1/100 c'est très significatif... alors on est juste.
Pour télécharger l'outil, fait par Quentin Leplat : https://messagedelanuitdestemps.org/publications-scientifiques/pi-phi-le-metre-et-la-coudee-royale-simple-coincidence-le-test-de-probabilite/
Compilation de valeur de coudées royale égyptiennes
Valeurs déduites de la mesure des pyramides de l’ancien empire :
- 52,374 cm : Pétrie à l’issue de plusieurs années d’arpentage et de mesure.
- 52,35 cm : Gilles Dormion.
- 52,33 à 52,375 : à partir des mesures de la base de la grande pyramide de Pétrie, Cole, Lehner et Dorner
Valeurs employées par différents auteurs (Historiens, Égyptologues, Anthropologues…) dans leurs études et publications :
- 52,39 cm : Newton, Dissertation upon the Sacred Cubit of the Jews.
- 52,37 cm : H. Carter, JEA 3 (1916): 150; Petrie, Pyramids and Temples, 181.
- 52,4 cm : J. J. Champollion-Figeac (1824, pp. 289–329) gave a value of 52.4 cm for the royal cubit in “Observations sur les coudées égyptiennes découvertes dans les mines de Memphis.”
- 52,3 cm : Armando Mei, Université de Naples : utilise la valeur 52,3 cm dans ses publications. (2018)
- 52,3 cm : Nora E. Scott, “Egyptian Cubit Rods”, Department of Egyptian Art, The Metropolitan Museum of Art Bulletin 2016, p. 1,
- 52,35 cm : Jean François Sagey : 1834, Traité de métrologie ancienne et moderne, Paris, Hachette.
- 52,31 cm : Carter, H.& Gardiner ,A.H., (1917).The tomb of Ramesses IV and theTurin plan of a royal tomb, JEA, Vol. 4 , pp. 130-158.
- 52,31 cm : Weeks, K.R., (1979).The Berkeley Map of the Theban Necropolis: Report of the Second Season, 1979, University of California, Berkeley.
- 52,3 cm : Monnier Franck, Petit Jean Pierre, The use of the ‘ceremonial’ cubit rod as a measuring tool. An explanation, 2016
- 52,5 cm : Budge, E.A.W., (1960). An Egyptian Hieroglyphic Dictionary, with an Index of English Words, King List and Geographical List with Indexes, List of Hieroglyphic Characters, Coptic and Semitic Alphabets, etc. Vol. I. A-Kha, Frederick Ungar Publishing Co., New York.
- 52,5 cm : Lepsius Die Längenmaße der Alten, (1884)
- 52,5 cm : Carlotti , (1995), ‘Quelques réflexions sur les unités de mesure utilisées en architecture pharaonique’, Les Cahiers de Karnak 10, pp. 127-140
- 52,37 cm, John Legon, qui s’appuie sur les travaux de Petrie pour comprendre l’implantation du complexe de Gizeh.
- 52,35 cm, Manu Seyfzadeh (DOI : 10.4236/ad.2018.62008 ), qui s’appuie sur la publication de Glen Dasch qui déduit de la grande pyramide une coudée dont la variation est comprise entre 52,30 cm et 52,38 cm. Dash, G. (2012). New Angles on the Great Pyramid.AERAGRAM, 13 , 10-19)
- 52,35 cm : Mark H. Stone, The Cubit, a history of measurement commentary. (Noté que cet auteur écrit que Dieter Arnold accorde à la coudée royale la valeur de 52,3 à 52,4 cm. page 3)
Source:
Voir aussi
- géométrie sacrée
- Nombre d'or
- Coudée royale égyptienne
- mètre
- Coudée de Nippur
- Liste d'unités de mesure
- Mesure des portes
- Funk Hellet => https://geobiologieblog.files.wordpress.com/2015/12/la-revue-du-caire-funk-hellet-12-26.pdf
- Ce qu'en pensent les zététiciens => https://irna.fr/La-coudee-Egyptienne-et-le-complot-metrique.html
- Analyse métrologique de la coudée royale Egytienne. http://messagedelanuitdestemps.org/wp-content/uploads/2017/10/Analyse-me%CC%81trologique-de-la-coude%CC%81e-royale-Egytienne..pdf
- les travaux de Jean-Pierre Petit sur la coudées royales égyptienne => https://www.jp-petit.org/science/Coudee_francais.pdf
- la coudée de Nippur une variante: https://messagedelanuitdestemps.org/metrologie-historique/de-la-coudee-de-nippur-a-la-coudee-egyptienne/
- https://fr.wikipedia.org/wiki/Syst%C3%A8me_de_mesure_ancien#Liens_externes
- http://regardsdupilat.free.fr/mesureprehistorique.html
- https://messagedelanuitdestemps.org/critique-des-theories-officielles-de-lhistoire/face-aux-chercheurs-alternatifs-historiens-et-les-archeologues-campes-sur-des-positions-fragiles/
- https://www.academia.edu/41264775/Extrait_Essai_Guillaume_Bergandi_Chapitre_3_La_Coud%C3%A9e_Royale_%C3%89gyptienne
C'est pas sorcier nous montre une canne des bâtisseurs: