Différences entre versions de « Quine des bâtisseurs »
(catégorie) |
(→les dimensions des sous unités : coudée de barabar) |
||
| (8 versions intermédiaires par le même utilisateur non affichées) | |||
| Ligne 1 : | Ligne 1 : | ||
[[Fichier:Quine-batisseurs-Pentagramme-nombre-dor-geometrie-sacree--15.png|thumb|300px]] | [[Fichier:Quine-batisseurs-Pentagramme-nombre-dor-geometrie-sacree--15.png|thumb|300px]] | ||
| + | [[File:Pige ou canne des batisseurs.jpg|thumb|Reconstitution d'une pige des bâtisseurs ou canne des bâtisseurs, issue de la quine d'unité de mesure: coudée, pied, empan, palme, paume]] | ||
La système de "quine des bâtisseurs" (aussi appelé parfois "pige des bâtisseurs" ) est construit sur la base d'une division en proportion dorée. (au lieu de la division décimale). | La système de "quine des bâtisseurs" (aussi appelé parfois "pige des bâtisseurs" ) est construit sur la base d'une division en proportion dorée. (au lieu de la division décimale). | ||
| Ligne 30 : | Ligne 31 : | ||
* pied : 32,36 cm | * pied : 32,36 cm | ||
* coudée: 52,36 cm | * coudée: 52,36 cm | ||
| + | |||
| + | On peut compléter avec l'étalon de [[Grottes de Barabar|Barabar]] qui veut 84,72 cm. | ||
| + | Puis dans la même logique on a 137,07, c'est marrant sachant que 137° est l'angle doré. La proportion dorée exprimée sur la circonférence d'un cercle. | ||
Vu que le nombre d'or permet une double progression géométrique (multiplication) ET arithmétique (addition), il est possible de déterminer les mesures des subdivisions également par des additions. | Vu que le nombre d'or permet une double progression géométrique (multiplication) ET arithmétique (addition), il est possible de déterminer les mesures des subdivisions également par des additions. | ||
| + | |||
| + | De la quine de base on peut dériver d'autres unités de mesures. | ||
| + | |||
| + | * Le pouce de 2,54 cm correspond à 1/3 de paume. | ||
| + | * Le yard correspond à 3 pieds, soit 0.97 m, ou la moitié d'une toise. | ||
| + | * La toise correspond à 6 pieds, soit, 1,941 mètre. | ||
| + | * Le [[mètre]] correspond à 5 empan. | ||
Soit: | Soit: | ||
| Ligne 57 : | Ligne 68 : | ||
Voir dans '''c'est pas sorcier''' à propos des cathédrales. Précisément à 14min: https://youtu.be/152Yprx1WDs?t=835 | Voir dans '''c'est pas sorcier''' à propos des cathédrales. Précisément à 14min: https://youtu.be/152Yprx1WDs?t=835 | ||
| + | |||
<youtube>https://youtu.be/152Yprx1WDs?t=835</youtube> | <youtube>https://youtu.be/152Yprx1WDs?t=835</youtube> | ||
| + | == Numérologie des constantes mathématiques == | ||
| − | + | Avec ce système de mesures, on obtient une cohérence stupéfiante des unités de mesures. On a là aussi un moyen numérologique d'exprimer des constantes mathématiques si on les exprimes en mètre ! (de la même manière que dans la [[chambre de Khéops]]... ) | |
| − | * | + | |
| − | * | + | * 5 empans de 20cm donnent 1 mètre. |
| − | * | + | * 5 pieds de 32,36 cm, soit le périmètre du pentagone inscrit dans le cercle, donnent 1,618 m le [[Nombre d'or|Nombre d'Or]] en [[mètre]]. |
| − | * | + | * 5 coudées de 52,36 cm donnent 2,618 m soit le carré du Nombre d'Or en mètre. |
| − | + | * 6 coudées de 52,36 cm donnent 3,1416 m soit la constante [[Pi]] exprimée en mètre. | |
| − | + | * 6 pieds de 32,36 cm valent 1 toise, soit 1,9416 mètre soit le rapport des deux constantes Pi et Phi. π/φ = 1,9416 | |
| − | + | ||
| − | + | On peut trouver ces rapports chez Christian Cambois... | |
| − | + | ||
| + | https://www.facebook.com/profile/100005596861299/search/?q=soit%201%2C9416%20m%C3%A8tre%20 | ||
| + | |||
| + | Voici un des ses livres qui évoque ces relations: "Homme et Ange noués: Dictées de l'au-delà et recherches intuitives " | ||
| + | https://amzn.to/43AgzYl | ||
== La pige et canne des batisseurs == | == La pige et canne des batisseurs == | ||
| Ligne 93 : | Ligne 110 : | ||
<youtube>https://www.youtube.com/watch?v=cTuQ9zC8Bws</youtube> | <youtube>https://www.youtube.com/watch?v=cTuQ9zC8Bws</youtube> | ||
| + | === sources === | ||
| + | * Jean-Pierre Gousset, Dessin technique et lecture de plan, Éditions Eyrolles, 2011, p. 103 | ||
| + | * Yves Chevalier et Céline Bryon-Portet, Petits essais de philosophie maçonnique concrète : Essais philosophiques, Primento, 2015, p. 47 | ||
| + | * https://fr.wikipedia.org/wiki/Ligne_(unit%C3%A9) | ||
| + | * https://fr.wikipedia.org/wiki/Pige_(mesure) | ||
| + | * http://www.eventdispatcher.fr/canne-des-batisseurs/ | ||
| + | * http://www.crcb.org/la-canne-de-larchitecte/.html | ||
| + | * https://au-vent-des-etoiles.sitego.fr/la-canne-des-batisseurs.html | ||
| + | * http://www.lieuxdenergies.fr/archives/2014/03/01/29336414.html | ||
| + | * https://www.trusatiles.org/2016/11/canne-d-architecte-de-maitre-batisseur-de-maitre-de-l-oeuvre.html | ||
| + | |||
| + | |||
| + | == Equerre des bâtisseurs == | ||
| + | [[Fichier:Triangle-des-bâtisseurs-origine-coudée-royale-égytienne.png|vignette]] | ||
| + | |||
| + | La pige présentée ci-dessus semble un outil très théorique et peu pratique. L'équerre des bâtisseurs semble bien plus pertinent, et on trouve des traces archéologiques et historique (dans des gravures) d'équerre, mais pas de pige ! | ||
| + | |||
| + | L'équerre des bâtisseurs est un outil pratique qui permet, avec un simple triangle issus d'un double carré de déterminer toutes les mesures de la quine des bâtisseurs. | ||
| + | |||
| + | C'est l'avantage du [[nombre d'or]]. C'est que les multiplications et divisions se remplacent par des additions et soustractions ! | ||
| + | C'est l'avantage de ce nombre qui est en même temps une suite géométrique et une suite arithmétique !! (on le voit bien avec la suite de fibonacci) | ||
| + | |||
| + | (On retrouve le même genre de raisonnement sur les règles à calcul qui utilisent la propriété des puissances pour remplacer des multiplications par des additions) | ||
| + | |||
| + | La taille de l'équerre est calibrée sur l'empan, soit la longueur entre le pouce et l'auriculaire écarté. Cette mesure semble normalisée à 20cm. | ||
| + | |||
| + | Donc on se retrouve avec un triangle de 1 empan (20cm) pour le long côté et un demi empan (10cm) pour le côté court. Du coup la diagonale du double carré, soit l'hypoténuse du triangle vaut √5 fois le petit côté. (22,360679775... cm) | ||
| + | |||
| + | En combinant ces longueurs on peut générer toutes les autres unités de mesure de la quines des bâtisseurs. | ||
| + | |||
| + | * La coudée = le périmètre du triangle de l'équerre | ||
| + | * Le pied = le petit côté + l'hypoténuse | ||
| + | * L'empan = le long côté | ||
| + | * La palme = hypoténuse + le petit côté - le long côté | ||
| + | * la paume = le long côté + le petit côté - hypoténuse | ||
| + | |||
| + | On retrouve ici aussi le principe de la suite de fibonacci. | ||
| + | |||
| + | Ces unités sont reliées entre elles par un facteur du nombre d'or. Ce qui permet de les retrouver par la suite de fibonacci: | ||
| + | * 1 paume + 1 palme = 1 empan | ||
| + | * 1 palme + 1 empan = 1 pied | ||
| + | * 1 empan + 1 pied = 1 coudée | ||
| + | |||
| + | J'explique l'équerre ici en vidéo: | ||
| + | |||
| + | <youtube>https://www.youtube.com/watch?v=0wkqocwcc-Q</youtube> | ||
== Références à creuser == | == Références à creuser == | ||
| Ligne 121 : | Ligne 184 : | ||
[[Catégorie:Unité de mesure]] | [[Catégorie:Unité de mesure]] | ||
[[Catégorie:Cathédrale]] | [[Catégorie:Cathédrale]] | ||
| − | [[Catégorie:Géométrie | + | [[Catégorie:Géométrie]] |
Version actuelle datée du 7 mars 2024 à 00:58
La système de "quine des bâtisseurs" (aussi appelé parfois "pige des bâtisseurs" ) est construit sur la base d'une division en proportion dorée. (au lieu de la division décimale).
C'est un système d'unité de mesure qui a été utilisé notamment pour la construction des cathédrales.
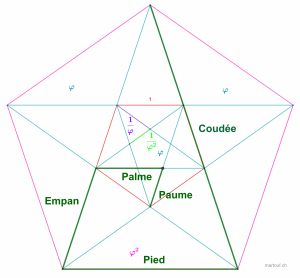
Il y a un lien entre les subdivision des unités de mesure paume, palme, empan, pied, coudée, c'est une progression géométrique et arithmétique de raison du nombre d'or.
Ainsi on peut déterminer les proportions par la géométrie sacrée dans une étoile inscrite dans une pentagone. C'est un pentagramme.
Ainsi nous avons un lien entre les subdivisions. (c'est déroutant pour nous qui sommes habitué à des subdivision décimale), mais il faut encore donne une taille, une échelle à ces proportions. Il y a 2 liens connus.
- L'empan fait 20cm. Soit 1/5 de mètre.
- La coudée est la même que la coudée royale égyptienne. Soit ~ 52,36.. cm
Les cahiers de Boscodon décrivent très bien ce système de mesure.
http://jayh1.free.fr/docs/livre/l_art_des_batisseurs_romans.pdf
C'est un cahier d'explication de la géométrie sacrée qui est basé sur les mesures et les tracés des abbayes de Boscodon et Sénanque.
les dimensions des sous unités
Ainsi avec la raison de nombre d'or, on peut déterminer la longueur équivalente en cm de chaque subdivision.
- paume : 7,64 cm
- palme : 12,36 cm
- empan : 20 cm
- pied : 32,36 cm
- coudée: 52,36 cm
On peut compléter avec l'étalon de Barabar qui veut 84,72 cm. Puis dans la même logique on a 137,07, c'est marrant sachant que 137° est l'angle doré. La proportion dorée exprimée sur la circonférence d'un cercle.
Vu que le nombre d'or permet une double progression géométrique (multiplication) ET arithmétique (addition), il est possible de déterminer les mesures des subdivisions également par des additions.
De la quine de base on peut dériver d'autres unités de mesures.
- Le pouce de 2,54 cm correspond à 1/3 de paume.
- Le yard correspond à 3 pieds, soit 0.97 m, ou la moitié d'une toise.
- La toise correspond à 6 pieds, soit, 1,941 mètre.
- Le mètre correspond à 5 empan.
Soit:
- 34 lignes dans une paume (lat. palmus minor)
- 55 lignes dans une palme (lat. palmus maior)
- 89 lignes dans un empan (une palme plus une paume)
- 144 lignes dans un pied (un empan plus une palme)
- 233 lignes dans une coudée (un pied plus un empan)
On retrouve là un extrait de la suite de Fibonacci qui est très utilisée dans la nature pour crée des proportions au nombre d'or. Il suffit de faire le rapport entre deux nombres consécutifs.
La création de la suite se fait en additionnant deux nombre consécutif pour trouver le suivant.
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987...
Ainsi on obtient une "canne royale" de 555 lignes de long.
Ces lignes permettent de créer d'autres unités de mesure intermédiaire comme le pouces ou le doigts.
- 864 lignes dans une toise (~= 24 paumes)
- 12 lignes dans un pouce (~= 1⁄3 paume)
- 9 lignes dans un doigt (~= 1⁄4 paume)
- 4 lignes dans un grain d'orge (~= 1⁄9 paume)
Voir dans c'est pas sorcier à propos des cathédrales. Précisément à 14min: https://youtu.be/152Yprx1WDs?t=835
Numérologie des constantes mathématiques
Avec ce système de mesures, on obtient une cohérence stupéfiante des unités de mesures. On a là aussi un moyen numérologique d'exprimer des constantes mathématiques si on les exprimes en mètre ! (de la même manière que dans la chambre de Khéops... )
- 5 empans de 20cm donnent 1 mètre.
- 5 pieds de 32,36 cm, soit le périmètre du pentagone inscrit dans le cercle, donnent 1,618 m le Nombre d'Or en mètre.
- 5 coudées de 52,36 cm donnent 2,618 m soit le carré du Nombre d'Or en mètre.
- 6 coudées de 52,36 cm donnent 3,1416 m soit la constante Pi exprimée en mètre.
- 6 pieds de 32,36 cm valent 1 toise, soit 1,9416 mètre soit le rapport des deux constantes Pi et Phi. π/φ = 1,9416
On peut trouver ces rapports chez Christian Cambois...
https://www.facebook.com/profile/100005596861299/search/?q=soit%201%2C9416%20m%C3%A8tre%20
Voici un des ses livres qui évoque ces relations: "Homme et Ange noués: Dictées de l'au-delà et recherches intuitives "
La pige et canne des batisseurs
A partir d'un système géométrique, il est possible de construire un étalon utilisable au quotidien.
Dans le film BAM, (Bâtisseurs de l'Ancien Monde) pascal waringo, un compagnon du tour de France explique la quine.
- https://www.batisseurs-medievaux.fr/snrb-mailhoc
- https://martouf.ch/2018/11/mes-notes-a-propos-du-documentaire-bam-les-batisseurs-de-lancien-monde/
Les archéologues du projet "Guedelon" de reconstruction d'un château philippien moderne, on recréé des cannes de bâtisseurs. Voir: Francis Gouge, « Guédelon. Le passé recomposé », in Le Monde, « Science & médecine », 18 septembre 2013, page 4
Tentative de retrouver le lien vers l'article: mais 16 septembre .. le même ?
=> https://www.lemonde.fr/sciences/article/2013/09/16/le-passe-recompose_3478549_1650684.html
sources
- Jean-Pierre Gousset, Dessin technique et lecture de plan, Éditions Eyrolles, 2011, p. 103
- Yves Chevalier et Céline Bryon-Portet, Petits essais de philosophie maçonnique concrète : Essais philosophiques, Primento, 2015, p. 47
- https://fr.wikipedia.org/wiki/Ligne_(unit%C3%A9)
- https://fr.wikipedia.org/wiki/Pige_(mesure)
- http://www.eventdispatcher.fr/canne-des-batisseurs/
- http://www.crcb.org/la-canne-de-larchitecte/.html
- https://au-vent-des-etoiles.sitego.fr/la-canne-des-batisseurs.html
- http://www.lieuxdenergies.fr/archives/2014/03/01/29336414.html
- https://www.trusatiles.org/2016/11/canne-d-architecte-de-maitre-batisseur-de-maitre-de-l-oeuvre.html
Equerre des bâtisseurs
La pige présentée ci-dessus semble un outil très théorique et peu pratique. L'équerre des bâtisseurs semble bien plus pertinent, et on trouve des traces archéologiques et historique (dans des gravures) d'équerre, mais pas de pige !
L'équerre des bâtisseurs est un outil pratique qui permet, avec un simple triangle issus d'un double carré de déterminer toutes les mesures de la quine des bâtisseurs.
C'est l'avantage du nombre d'or. C'est que les multiplications et divisions se remplacent par des additions et soustractions ! C'est l'avantage de ce nombre qui est en même temps une suite géométrique et une suite arithmétique !! (on le voit bien avec la suite de fibonacci)
(On retrouve le même genre de raisonnement sur les règles à calcul qui utilisent la propriété des puissances pour remplacer des multiplications par des additions)
La taille de l'équerre est calibrée sur l'empan, soit la longueur entre le pouce et l'auriculaire écarté. Cette mesure semble normalisée à 20cm.
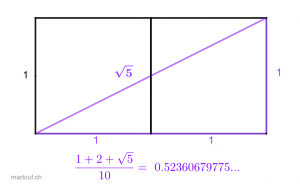
Donc on se retrouve avec un triangle de 1 empan (20cm) pour le long côté et un demi empan (10cm) pour le côté court. Du coup la diagonale du double carré, soit l'hypoténuse du triangle vaut √5 fois le petit côté. (22,360679775... cm)
En combinant ces longueurs on peut générer toutes les autres unités de mesure de la quines des bâtisseurs.
- La coudée = le périmètre du triangle de l'équerre
- Le pied = le petit côté + l'hypoténuse
- L'empan = le long côté
- La palme = hypoténuse + le petit côté - le long côté
- la paume = le long côté + le petit côté - hypoténuse
On retrouve ici aussi le principe de la suite de fibonacci.
Ces unités sont reliées entre elles par un facteur du nombre d'or. Ce qui permet de les retrouver par la suite de fibonacci:
- 1 paume + 1 palme = 1 empan
- 1 palme + 1 empan = 1 pied
- 1 empan + 1 pied = 1 coudée
J'explique l'équerre ici en vidéo:
Références à creuser
- https://fr.wikipedia.org/wiki/Grain_(unit%C3%A9)
- https://fr.wikipedia.org/wiki/Anciennes_unit%C3%A9s_de_mesure_fran%C3%A7aises
- https://fr.wikipedia.org/wiki/Anciennes_unit%C3%A9s_de_mesure_fran%C3%A7aises#Unit%C3%A9s_de_longueur
- https://fr.wikipedia.org/wiki/Canne_(unit%C3%A9)
- https://books.google.fr/books?id=RQP2c4uyz9oC&printsec=frontcover#v=onepage&q&f=false
- https://fr.wikipedia.org/wiki/Pige_(mesure)
- https://www.ledifice.net/7033-4.html
- https://web.facebook.com/howard.crowhurst/posts/2161669153954326?_rdc=1&_rdr
- https://martouf.ch/2018/07/le-nombre-dor-base-systeme-unite-mesure/canne-des-batisseurs-de-cathedrale/
Réfutation de notre zététicien préféré