Coudée locale
La coudée locale est une unité de mesure propre à la latitude d'un lieu.
Il s'agit du cosinus de l'angle de la latitude courante.
Par exemple à la latitude de 45° => le cosinus (45°) = √2/2 => soit la moitié de la diagonale d'un carré de 1 mètre. => 70,71... cm
https://www.wolframalpha.com/input/?i=cos%2845%29
Résonance entre le lieu et l'édifice
En astro-géométrie, c'est une pratique courante de marquer au sol des formes géométriques liées à la latitude d'un lieu. C'est une manière de faire entrer en résonance le lieu et la construction. Une manière de créer de l'harmonie.
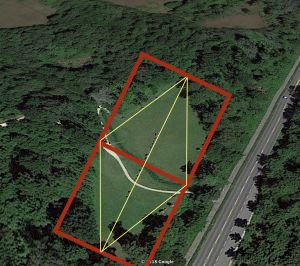
Une manière de faire est le rectangle solsticial qui marque la course du soleil à une latitude donnée.
Une autre manière de faire est d'utiliser une unité de mesure propre à la latitude du lieu. C'est ce qu'on appelle la coudée locale.
La coudée locale des menhirs de Clendy
Un bel exemple de coudée locale se trouve à Yverdon avec les alignements de menhirs de Clendy. https://fr.wikipedia.org/wiki/Alignement_de_Clendy
C'est un site qui date de -4800, l'architecte et chercheur en géobiologie Stéphane Cardinaux a fait un relevé du schéma directeur. Il s'agit d'un double carré. Une forme très courante en géométrie sacrée. On la trouve notamment à la base de la chambre de Khéops de la grande pyramide de Gizeh.
Le double carré des menhirs de Clendy a une dimension de 47.9 mètre pour le côté d'un carré.
- https://www.geniedulieu.ch/78-genie-du-lieu/98-qu-est-ce-que-la-geometrie-sacree
- https://www.ursusmajor.ch/downloads/megalithanlage-yverdon-clendy-v-4_7.pdf
Le site des menhirs de Clendy est à la coordonnée: 46.7774, 6.6569
Cosinus(46.7774°) = 68,4835
=> https://www.wolframalpha.com/input/?i=cos%2846.7774%29&assumption=%22TrigRD%22+-%3E+%22D%22
La coudée locale est donc de 68,4835 cm.
Donc la mesure de 47.9 mètre correspond à 47,9/0,684835 = 69.9438 coudées locales => on peut raisonnablement arrondir à 70 coudées locales.
Le 7 étant un nombre récurrent sur ce site quand on l'étudie du point de vue de la géobiologie. (7 lignes H de chaque côté de l'axe centrale et 21 lignes H de chaque côté du petit axe), on peut raisonnablement penser que la volonté des bâtisseurs était de marquer 70 coudées locales pour le côté du carré.
Source: livre de Stéphane Cardinaux: Géométries sacrées. p.214
Détermination de la coudée locale
Comment déterminer la coudée locale d'un lieu ?
C'est simple, il suffit de positionner un bâton de 1 mètre, dans la direction de l'étoile polaire et la projection au sol du bâton (le cosinus de l'angle) marque la coudée locale.
En fait l'angle de la hauteur l'étoile polaire par rapport à l'horizon indique l'angle de la latitude. Puis on prend la projection au sol, (le cosinus) pour obtenir la coudée locale.
On peut aussi utiliser le soleil, mais il faut sa position la plus haute, soit lors du solstice d'été. De là, soit on procède comme avec l'étoile polaire, en pointant le bâton en direction du soleil et en mesurant sa projection au sol. Soit on peut aussi planter le bâton (gnomon) dans le sol verticalement et mesurer la longueur de l'ombre.
Donc la technique est simple et ne nécessite par de calcul pour déterminer la coudée locale d'un lieu.
Cependant, le bâton doit avoir la longueur de 1 mètre ..... comment est-ce possible il y a 6000 ans ??? ... c'est l'enquête que je mène... voir la page dédiée au mètrear...
- https://fr.wikipedia.org/wiki/Gnomon
- https://fr.wikipedia.org/wiki/Histoire_de_la_navigation_astronomique