- Comme tout le monde, je l'utilise tous les jours, quand je fais des achats, quand je me déplace.
- Comme tout le monde, je croyais tout savoir de lui.
- Comme tout le monde, je pensais que son origine n'avait aucun mystère…
- A l'école d'ingénieur, je pensais qu'on m'avait tout appris de lui…
Jusqu'au jour où j'ai découvert que des faits inexpliqués restaient ignorés par les historiens et les archéologues…

Le Mètre est universel, il est omniprésent. Il est avec nous ici, en ce moment même. Tu le vois chaque fois que tu regardes par la fenêtre ou lorsque tu allumes la télévision. Tu ressens sa présence quand tu pars au travail, quand tu vas à l'église, ou quand tu paies tes factures.... 💊
Regardes autour de toi, je suis certain qu'il est là et que tu ne fais même plus attention à lui..
Il a servi à confectionner tes habits..
Il a servi à dimensionner la pièce et les meubles qui t'entourent..
Il porte bien son nom de maître....
La vérité sur le mètre...
Si tu veux rester dans tes croyances, c'est le moment de quitter cette page, tu pourra faire des beaux rêves et penser ce que tu veux.
Si tu veux continuer de découvrir l'origine de cette matrice qu'est le mètre, alors continue la lecture et partons à l'aventure.
N'oublie pas, je ne t'offre que la vérité, rien de plus.
- Nous irons en pleine révolution française découvrir la philosophie qui motive et anime vraiment les révolutionnaires.
- Nous nous intéresserons à leurs lectures....
- Nous irons voir pourquoi Gaspard Monge, un des 5 membres de la commission qui a déterminé la définition du mètre a pillé les bibliothèques du Vatican, de Venise, Bologne et de Pavie.... Il a ramené en France des livres anciens et des papyrus égyptiens.
- Nous verrons que de nombreux monuments anciens dans le monde ont des dimensions en mètre !! Ceci sans que les archéologues ne s'en préoccupent !
- C'est le cas notamment des pierres angulaires de plusieurs cathédrales.
- Nous explorerons pourquoi de nombreux protagonistes de l'histoire du mètre se sont intéressés à la pyramide de Khéops....
- ... Jusqu'au point que Napoléon lui même est allé voir les pyramides, avec son armée, mais aussi avec 167 scientifiques recrutés par le même Gaspard Monge évoqué ci-dessus.
- Pourquoi avoir besoin d'autant de scientifiques pour mener une guerre ?
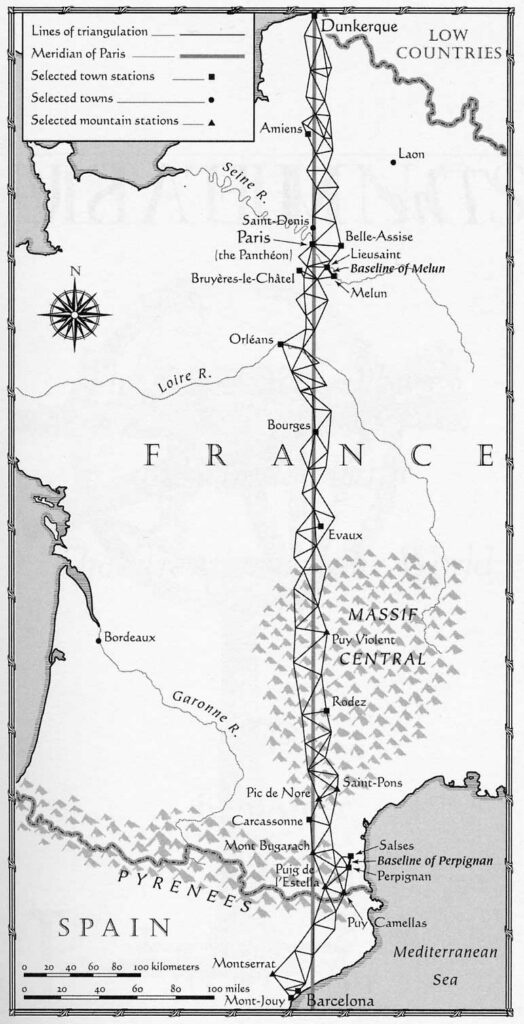
- Nous évoquerons le récit de l'aventure rocambolesque de la mesure du méridien entre Dunkerque et Barcelone par Méchain et Delambre... et de la terrible erreur faite par Méchain qui l'a rendu suicidaire.... Il voulait brûler ses carnets... sa femme a du venir le chercher dans un monastère abandonné dans les montagnes au dessus de Barcelone où il s'était reclus....
- Fait également étrange, que faisait le fils Méchain en égypte et pourquoi il est rentré plus tôt que les autres de la campagne d'égypte ?
- Nous verrons aussi que le postulat de base de la mesure du méridien entre Dunkerque et Barcelone était voué à l'échec... et n'a pas pu être utilisé !! (contrairement à ce que nous disent la plupart des livres d'histoire !)
- Nous étudierons le rôle joué par les Francs Maçons dans cette histoire. Quand on pense à eux, on pense tout de suite à l'équerre et au compas. Mais un autre outil de maçon, le fil à plomb est peut être plus important dans cette histoire.
1er épisode de la saga....
Le sujet est vaste, il faut quelques prémices de base pour bien comprendre de quoi on parle... et c'est peut être par manque de connaissances de base que finalement personne pendant 200 ans n'a remarqué qu'il y a des "bugs" dans l'histoire de la création du mètre !
Voici une petite vidéo facultative qui pose le décors et montre à l'aide d'un pamplemousse les bases des moyens de repères sur notre planète. Qu'est-ce qu'un méridien, un équateur, une latitude, une longitude....
Si tu veux creuser encore plus sur les outils de "navigation" sur notre planète.... voici cette page...
Mais commençons plutôt par le 1er épisode de la saga du mètre. Nous allons remettre en forme la chronologie des événements, ceci pour avoir des faits solides sur lesquels ensuite découvrir la véritable origine du mètre...
C'est parti dans le Terre-ier du Lapin blanc.....
Résumé des points clés sur l'origine du mètre en vidéo
La définition du mètre a été changée
Si l'on cherche la définition actuelle du mètre on va nous indiquer que c'est "la longueur du trajet parcouru par la lumière dans le vide pendant une durée d'un 299 792 458e de seconde"
C'est une définition issue d'un raisonnement circulaire, car le nombre 299 792 458 est en fait la vitesse de la lumière en mètre par seconde !
La définition d'origine, établie durant la révolution française, n'est pas ça du tout. C'est le 10 000 0000 ème du 1/4 du méridien, la circonférence de la Terre qui passe par les pôles. (la définition du méridien aussi a changée, maintenant elle désigne la moitié du cercle d'un pôle à l'autre)
La définition du mètre nécessite donc de mesurer la circonférence de la Terre.
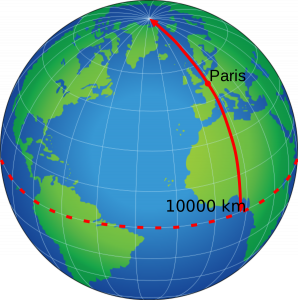
Chronologie de l'histoire d'une mesure universelle
vers -200
Eratosthène, alors à la tête de la bibliothèque d'Alexandrie, mesure la circonférence de la Terre avec une précision inégalée pendant 2000 ans: 39 375 km (aujourd'hui on mesure la circonférence qui passe par les pôles à 40 007,864 km)
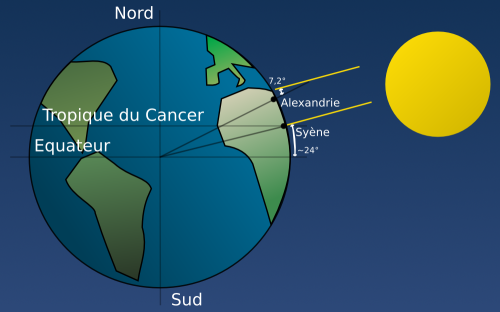
829
Le Calife Al-Ma'mūn crée l'observatoire de Bagdad. Il engage de nombreux scientifiques qui collectent et traduisent des textes scientifiques, notamment perses et grecs. Afin de vérifier les théories astronomiques de l'époque Al-Ma'mūn fait mesurer la circonférence de la Terre. Ses arpenteurs déterminent 37 000 km.
C'est également sous le règne de Al-Ma'mūn que vécu le mathématicien Al-Khwârizmî dont le nom a donné le mot "algorithme". Ce dernier est celui qui a importé d'Inde le zéro et la notation positionnelle décimale et l'a diffusée dans tout le monde arabe. (Ce qui nous fait appeler à tord les chiffre que nous utilisons des "chiffres arabes").
832
Le Calife Al-Ma'mūn visite les pyramides de Gizeh à la recherche de trésors. l'égyptologue Salima Ikram nous explique que Al Mamoun ne cherchait pas n'importe quel trésor... mais des cartes du monde et des objets magiques. (Probablement ceux décrits dans le papyrus Westcar). Peut être que le Calife voulait confirmer sa mesure de la Terre ?
L'entrée de la pyramide de Khéops, actuellement utilisée par les touristes est attribuée à Al Mamoun. Cependant l'explication n'est pas exacte. Al-Mamoun n'a pas créé le passage, il l'a juste agrandi.
Murtada Ibn al-Khafîf a écrit sur l'entrée dite d'al-Ma'moun, de la Grande Pyramide : "Le Commandeur des Fidèles le Mamune [al-Ma'moun], Dieu lui fasse miséricorde, étant entré dans le pays d'Égypte, et ayant vu les Pyramides, eut envie de les démolir , pour le moins quelqu'une d'elles, afin de savoir ce qui était dedans. Sur quoi on lui parla ainsi : Vous désirez une chose qui ne vous est pas possible. Si vous l'entreprenez et que vous n'en veniez pas à bout, ce sera une honte au Commandeur des Fidèles. À quoi il répondit : Je ne puis me passer d'en découvrir quelque chose. Il fit donc travailler à la brèche qui y était déjà commencée, et y fit de grandes dépenses." - p.50 de l'égypte de Murtadi fils du gaphiphe. (ibn-el-afif)
Il est plus logique qu'il ait élargit la brèche, car sur 920m de périmètre ce serait un sacré coup de chance de tomber juste là où il y a les couloirs et en plus de passer du bon côté pour contourner les bouchons de granit. La brèche devait probablement être une sortie plutôt qu'une entrée !
995
Le mathématicien, astronome, physcien, philosophe (etc..) persan Al-Biruni calcula le rayon de la Terre à 6 339,6 km (ce résultat fut utilisé en Europe au XVIe siècle). La méthode est originale, Il part du principe bien sage que les angles sont facile à mesurer, mais les distance difficile à évaluer. Dans le sud du Khwārizm, sur la rive gauche de l'Amū Daryā, il mesure la hauteur d'une montagne par des visées à l'astrolabe. Puis, depuis le sommets de la montagne, bien à angle droit à l'aide d'un fil à plomb, il mesure l'angle de l'horizon. Le reste n'est que calcul de trigonométrie.
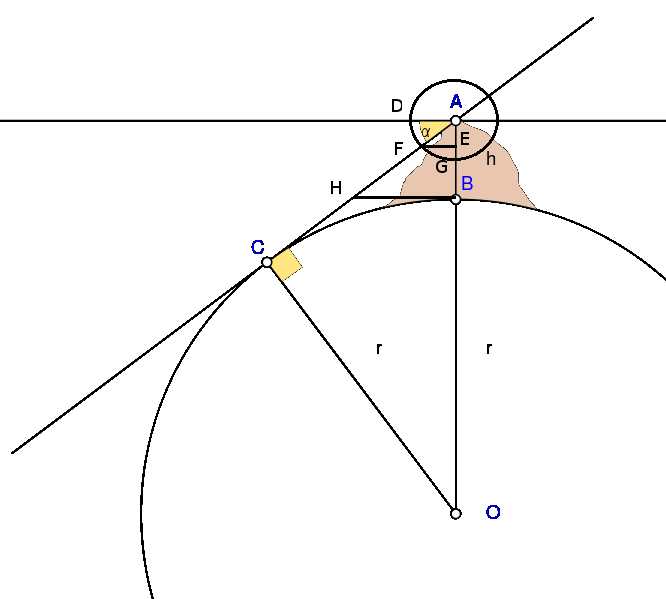
Al-Biruni laisse le premier écrit qui subdiviser l'heure de manière sexagésimale en minutes, secondes, tiers et quarts, en 1000, lors d'une discussion sur les mois juifs.
1528
Le médecin du roi de France Henri II, Jean Fernel publie Cosmotheoria un livre dans lequel il décrit comment il a mesuré un degré de méridien entre Paris et Amiens. Il a compté le nombre de tours de roue de sa voiture, soit 17024. De là il détermine un degré de méridien de 340480 pieds soit 56 746 toises (1,959m) donc 40 019 km. Une précision impressionnante !
Plusieurs essais ont été fait les siècles suivants, mais pas avec autant de précision. Pour le détail des essais voir cette chronologie des mesures de la Terre.

1583
Galileo Galilei, âgé de dix-neuf ans, découvre, en chronométrant à l'aide de son pouls, la régularité des oscillations des lustres de la cathédrale de Pise. De retour chez lui, il compare les oscillations de deux pendules et travaille à la loi de l'isochronisme des pendules, dont le Néerlandais Christian Huygens découvrira la vraie loi de l'isochronisme rigoureux en 1659.

Grâce à Euclide, qui l'éblouit, Galilée réoriente ses études de médecine vers les mathématiques. Dès lors, il se réclame de Pythagore, de Platon et d'Archimède et contre le géocentrisme aristotélicien.
1585
L'ingénieur, mathématicien, physicien néerlandais Simon Stevin publie en français la traduction de son petit traité "De Thiende" (la disme) dans L'arithmétique.
Stevin fait la promoton du système décimal. Il déclare que l'utilisation universelle du système décimal est inéluctable.
Il propose une notation dans la quelle les décimales sont affectées de leur puissance de dix, marquées par un petit cercle autour de l'exposant. Une notation qui ne sera pas très utilisée.
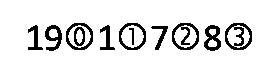
Son traducteur en latin est Willebrord Snell (souvent dit Snellius). Voir ci-dessous.
1617
Le mathématicien, physicien néerlandais Willebrord Snell, dit Snellius se veut être le nouvel Eratosthène batave. Il calcule le rayon de la Terre.
Il mesure le 1° de méridien entre les villes d'Alkmaar et de Berg-op-Zoom, via 14 points de triangulation. C'est la première mesure opérée par triangulation.
Il obtient 107,395 km la valeur actuellement mesurée étant de 111,281 km.
Il fait partie d'un comité pour déterminer les instruments de navigation pour la marine Hollandaise. Dans ce comité on retrouve Simon Stevin, qui fait la promotion du système décimal.
C'est un élève de Joseph Juste Scaliger. Durant ses voyages en Europe, à Prague, il rencontre notamment Tycho Brahe et Kepler.
1636-1640
L'astronome anglais John Greaves a appris les langue orientales en s'intéressant aux œuvres des astronomes de l'Antiquité orientale. Il enseigne à Oxford. Il collecte des manuscrits grecs et arabes pour le compte de l'archevêque de Canterbury.
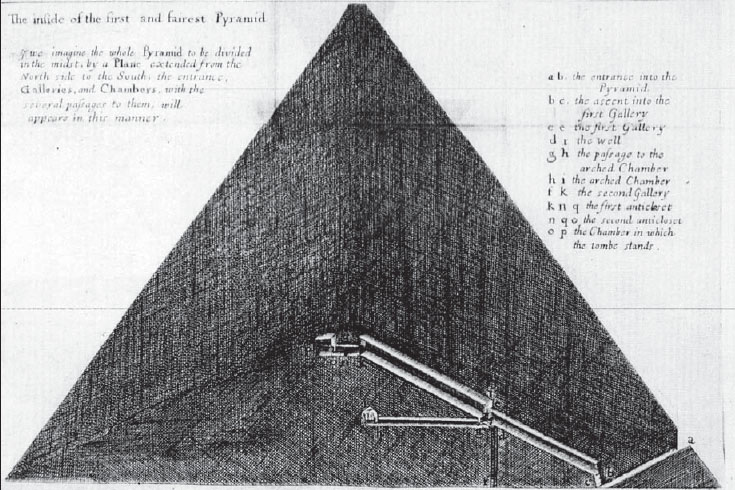
En 1636 il part en voyage à Rome puis en égypte. Il a pour objectif de cataloguer toutes les mesures utilisées dans le monde antique et moderne, et d'en décrire les valeurs et les relations. En 1639 il visite et mesure les pyramides. En 1646 il publie un livre avec ses mesures de la grande pyramide de Gizeh. "Pyramidographia, or, A description of the pyramids in Ægypt"
1644
Marin Mersenne, un moine français publie le livre Cogitata physico-mathematica dans lequel il propose d'utiliser le pendule comme base pour une unité de mesure de longueur.
Mersenne est un érudit qui a déjà publié en 1633 un livre nommé Harmonie universelle, pendant longtemps une référence dans le domaine de la musique. Ce livre se base notamment sur les découvertes acoustiques de Vincenzo Galilei, le père de Galileo avec qui Mersenne correspondait.
En 1626, Mersenne se lie d'amitié avec René Descartes et publie des traductions d'Euclide, d'Apollonius de Perge (qui habitait Alexandrie), d'Archimède, de Serenus, de Ménélas et de Maurolycus. Il aime comparer les théories des anciens et des modernes.
En 1635 Mersenne crée l'Academia Parisiensis, une académie dans laquelle par ses lettres et les réunions qu'il organise, il met en contact 140 savants et préfigure l'académie des sciences et le système de publication scientifique.
1658
Le Hollandais Christian Huygens, membre de l'académie de Mersenne, travaille sur le pendule oscillant dans l'idée de réguler des horloges. Il découvre la formule de l'isochronisme rigoureux en décembre 1659 : lorsque l'extrémité du pendule parcourt un arc de cycloïde, la période d'oscillation est constante quelle que soit l'amplitude.
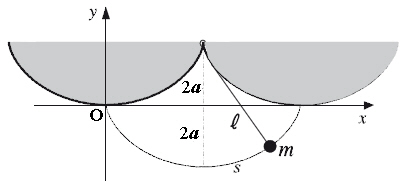
(Pour le côté cycloïde, il s'aide des travaux de l'architecte anglais Christopher Wren, un personnage passionnant, également co-fondateur de la Royal Society, qui a construit la moité de Londres ! Surtout après le grand incendie de 1666. Il méritait bien son intégration chez les francs Maçons. Il a notamment construit 51 églises et la cathédrale St-Paul, mais aussi l'observatoire de Greenwich qui marque le méridien d'origine actuel)
Huygens détermine la période du pendule simple. Soit:
T = 2π √l/g
Il commence a imaginer que la force centrifuge due à la rotation de la Terre modifie la pesanteur suivant la latitude. Il imagine que la Terre n'est pas une sphère. Mais qu'elle est aplatie. (Il publiera ces idées 28 ans plus tard)
1660
La Royal Society de Londres envisage, d'utiliser la longueur d'un pendule battant la seconde comme base d'une unité de longueur selon une proposition de Christian Huygens et Ole Christensen Rømer qui suivent l'idée déjà formulée en 1644 par Marin Mersenne. C'est là le début du mètre avec son ordre de grandeur actuel.
=> Le mètre serait-il anglais ?
1666 (ou juste avant)
L'anglais John Wilkins, membre co-fondateur de la Royal Society, propose l'adoption d'une mesure universelle (universal measure), d'unités décimales, basée sur le principe d'un pendule battant une seconde, et dont la longueur fondamentale est de 38 pouces prusses (1 prussian inch = 26,15 mm), soit de 993,7 mm (ou 39,25 pouce de Londres). Il publie cette idée en 1668, mais ce n'est que la seconde édition, car tous les exemplaires imprimés de la 1ère ont brulés dans le grand incendie de Londres en 1666.
1666
Publication de la traduction française du livre "L'Égypte de Murtadi"(où il est question des pyramides, du débordement du Nil & autres merveilles de cette province..). C'est la traduction par Pierre Vattier, professeur du roi en langue arabique. C'est la traduction d'un livre en arabe de l'égyptien Ibn al-ʿAfīf, Murtaḍá ibn Ḥātim ibn al-Musallam (1154-1237). Ce manuscrit faisait partie de la bibliothèque du cardinal Mazarin.

1668
L'abbé Picard propose le pied universel qui vaut 1/3 de la longueur d'un pendule qui bat la seconde.
1669
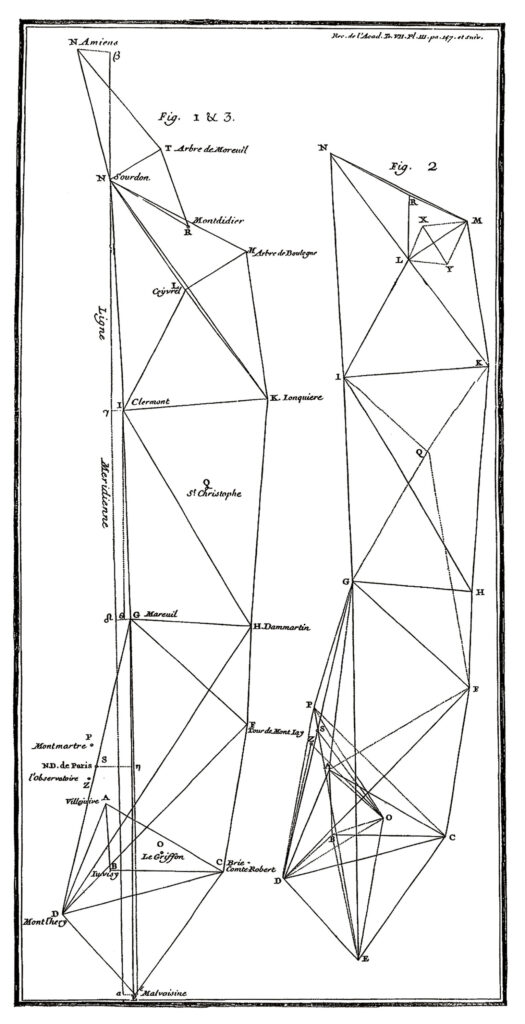
L'abbé Picard mesure un arc de méridien, afin de mesurer la Terre et dans le but défini par Colbert de cartographier la France de façon géométrique. La région choisie se trouve à l'est de Paris, entre Malvoisine et Sourdon-Amiens. Le livre Mesure de la Terre par l'abbé Picard. C'est la base de la Méridienne de France.
1670
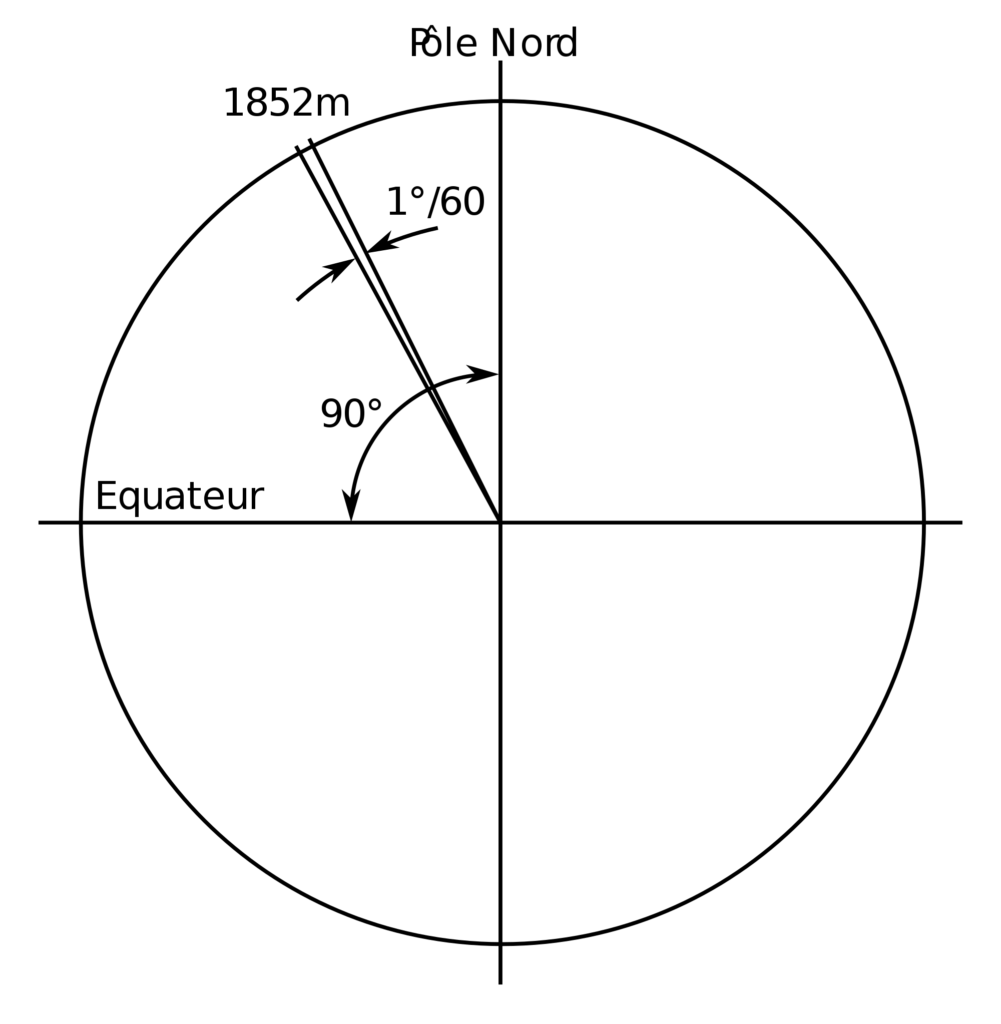
Gabriel Mouton propose d'utiliser la base 10 comme division d'une unité de mesure universelle qu'il appelait virga, (la verge). Cette unité correspond à un millième de la longueur d'une minute d'arc de méridien ~1,8m.
(La longueur moyenne d'une minute d'arc de méridien étant de 1852 mètres. Cette longueur est de nos jours le mille nautique. )
1675
L'italien Tito (Livio) Burattini publie un livre nommé "Misura universale" dans lequel il reprend l'idée vue chez John Wilkins du pendule comme base d'une mesure universelle. Il traduit "universal measure" par "metro cattolico".
Dans la préface du livre "Misura universale", Burattini décrit sa visite de la grande pyramide de Gizeh en 1639 avec John Greaves, l'astronome anglais spécialisé en métrologie ancienne cité plus haut. Burattini propose tout un système d'unité de mesure reliées entre elles.
"Après avoir pris toutes les mesures dont nous disposons, M. Graves a éclaté en ces termes, oh combien le monde souffre de ne pas savoir combien de mesures des anciens Egyptiens sont contenues dans la longueur et la largeur de cette pièce, ou du moins de la Zone, dont nous connaissions la longueur de la mesure égyptienne. Donc, puisque nous ne gardons pas ces souvenirs, assurons-nous au moins que cette structure, qui durera plusieurs milliers d'années, soit comparée et proportionnée à la mesure de ma patrie"
Burattini se dit inspiré par sa visite de la pyramide de Khéops:
"bien que je ne pense à rien d'autre, sauf à établir une mesure prise depuis la chambre haute, et depuis l'arche de la Pyramide égyptienne placée la plus près du Nil : mais rien de moins que le désir, que j'ai vu dans ces deux grandes figures, de perpétuer les mesures et les poids m'a tellement stimulé que de temps en temps, j'y pense de plus en plus, et je l'ai enfin mis en place ; je ne sais pas si je serai arrivé à l'approbation universelle ;"

Burattini base tout sa défintion du mètre sur un pendule qui bat la seconde.
Il trouve une mesure correspondant à environ 993,9 mm actuels. (c'était avant la théorie de la gravitation de Newton et la compréhension que la longueur d'un pendule varie avec la latitude à cause de l'effet de la gravité)

1680 (environ)
Le grand savant Isaac Newton, étudie les mesures de la pyramide de Khéops, notamment dans le livre de John Greaves, Pyramidographia, or, A description of the pyramids in Ægypt, George Badger, London, 1646. (mentionné plus haut)
Il recherche la valeur précise de la circonférence de la Terre pour valider sa théorie de la gravité. Pour ce faire, il pensait devoir trouver la valeur précise de l'unité de mesure qui a été utilisée pour construire la pyramide, la coudée royale égyptienne qu'il nomme: "Cubiti Regii".
Newton a entendu parlé de la circonférence de la Terre donnée par Thales et Anaximandre au VIe siècle avant J.-C., soit 400 000 "stades". Mais comme la mesure du stade s'est perdue, il cherche à la retrouver grâce à la coudée royale égyptienne.
Ainsi Newton compare bon nombre de mesures, et écrit les conversions dans d'autres unités de mesures, comme le pied romain, le pied drusien, ou la coudée des hébreux dont il recherche également la valeur afin de déterminer la mesure du exacte du temple de Salomon.
On peut lire dans le manuscrit de Newton qu'il pense que la coudée vaut 1/100 de la largeur de la pyramide. (Ce qui ne fonctionne pas !)
Newton utilisera pour finir la mesure du degré de méridien effectuée par l'abbé Picard en 1669.

Newton n'est pas passé loin de trouver la circonférence de la Terre en étudiant la pyramide de Khéops. Il est maintenant étonnant de voir la similitudes des nombres de 400 000 stades et de 40 000 km pour la mesure de la circonférence de la Terre. (à 7km près d'après les mesures les plus récentes du méridien)
Selon cette idée, un stade vaudrait donc 100 mètres !
Plus loin, on verra qu'en 1780 Paucton publiera un traité de métrologie où il reprend des sources anciennes qui disent que le côté de la grande pyramide vaut 1 stade. Newton pensant qu'il devait trouver une unité de mesure qui vaut 1/100 du côté de la pyramide, soit 1/100 d'un stade aurait trouvé là le mètre !!!
Le soucis, c'est que la pyramide fait 230m de côté et pas 100.. et que Newton cherchait la coudée royale, qui vaut 0.5236 m.
Il est à préciser que Newton était en plus d'un grande scientifique, un grand alchimiste (raison pour laquelle Newton était aussi le chef de la monnaie royale, les rois engageant souvent des personnes capables de transformer le plomb en or pour gérer la monnaie...).
1720
L'astronome Jacques "Cassini dans le livre De la grandeur, et de la figure de la terre pages 158 et 159, proposoit un pied géométrique qui seroit la six-millième partie de la minute du grand cercle, ou bien une brasse de deux de ces pieds et qui seroit là dix-millionième partie du demi-diamètre de la terre, ou enfin une toise de six de ces: mêmes pied ensorte que le degré eût été de 60 060 toises."
C'est par ses mots que Delambre, dont nous parlerons plus loin, raconte la proposition de Jacques Cassini de crée une unité de mesure universelle basée sur le rayon de la Terre.

1735 - Expéditions géodésiques françaises
Entre 1735 et 1744 Charles Marie de La Condamine, mandaté par l'académie des sciences, mène une expédition à Quito en équateur pour mesurer les 3 premiers degrés de méridien depuis l'équateur et ainsi déterminer la figure de la Terre. Est-elle aplatie aux pôles comme le prétend Newton, ou à l'équateur comme le prétends Descartes ?
Ce sont les expéditions géodésiques françaises.
Ainsi deux équipes sont envoyées mesurer des méridiens près des pôles et près de l'équateur (pour avoir les plus grande différences). Finalement c'est Newton qui avait raison: la Terre est aplatie aux pôles. Dès 1737, on considère que la Terre est une ellipsoïde.
1748
Pendant son expédition en équateur, Charles Marie de la Condamine imagine un étalon universel de longueur basé sur un pendule qui bat la seconde. Mais pas n'importe où, à l'équateur. (439.15 lignes)
Il présente cette idée à l'académie des sciences le 24 avril 1748 et elle sera publiée en 1776 dans un livre publié après sa mort en 1774.

1766
Mathieu Tillet réalise une soixantaines d'étalon de la Toise du Pérou (la toise utilisée pendant l'expédition de la Condamine au Pérou), et la diffuse dans toute la France.
1774
Turgot, contrôleur des Finances, propose au marquis de Condorcet le travail difficile d'unification des mesures. Mais en 1776 Turgot est remplacé par Necker et la réforme est abandonnée.
1780
Alexis-Jean-Pierre Paucton publie un traité de métrologie dans lequel il prétend que les anciens avaient déjà mesuré la taille de la Terre et tiré de là une unité de mesure universelle de laquelle toutes les autres sont dérivées. Paucton prétend que cette unité de mesure originelle est conservée en égypte. Ainsi il montre, sur le papier, que le côté de la grande pyramide de Gizeh vaut 1 stade et que le degré de méridien à cette latitude vaut 500 stades, soit 500 fois le côté de la grande pyramide.
"D'où je conclus que le côté de la base de la grande pyramide étoit d'un stade juste tel qu'il est défini par Marin de Tyr, par Ptolémée & par Héron."

En 1806 Delambre réfutera les calculs de Paucton sur la base de mesures toutes fraiches de la pyramide faites par les savants de la campagne napoléonienne en égypte.
J'ai personnellement aussi tenté de reprendre les calculs de Paucton, mais bien que le ordres de grandeurs soit souvent assez juste, je ne trouve rien qui colle vraiment.
Cependant, en 1817 Edmée Jomard qui a participé au mesures de la Grande pyramide de memphis, confirmera qu'il y a un lien entre le degré de méridien et le périmètre de la pyramide.
On verra ceci plus loin, mais pour le moment revenons aux propos de Paucton:
"Je prouve que les Anciens avoient un étalon naturel de mesure, pris dans la grandeur d'un degré du méridien, & que dès les temps ses plus reculés, à remonter même avant la fondation de Ninive, de Babylone & des Pyramides d'Egypte, la circonférence de la Terre avoit été mesurée aussi exactement qu'elle l'a été dans ce siécle ; démontre que cet étalon immatriculé dans la nature & de la valeur de la quatre-cent-millieme partie d'un degré du méridien , étoit universel & commun à l'Asie, à l'Afrique & à l'Europe, à quelques exceptions près ; qu'il étoit celui des Perses, des Arabes, des Juifs, des Egyptiens, des Espagnols qui l'ont conservé jusqu'à ce jour presque dans son intégrité, des Gaulois , des Bretons & des Germains ou Allemands, chez qui on le retrouve encore aujourd'hui dans la plupart des Villes les plus considérables…."


1787
Volney publie son livre "Voyage en Syrie et en Égypte, pendant les années 1783, 1784 et 1785" (et le tome 2). Ces récits de voyage et la mention des pyramide d'égypte, attise l'intérêt du public pour l'égypte. C'est surtout l'ouvrage suivant de Volney, pulbié en 1791: Les ruines, ou Méditation sur les révolutions des empires qui influencera un certain Talleyrand. (On en reparlera plus loin...)
Volney est tout un personnage. Il arrive a Paris à 19 ans vers 1777. Il y rencontre des personnages comme Condorcet et Diderot. Il prend part à la réception de Benjamin Franklin, ce père fondateur des USA étant le 1er ambassadeur des USA en France entre 1778 et 1785. Ces grands esprits libres confortes l'athéisme et le matérialisme de Volnay. Il décrit par exemple le christianisme comme un culte à une allégorie solaire.
De ses études de médecine, il retiendra surtout l'envie d'apprendre les langues orientales et d'aller enquêter sur le terrain des récits bibliques pour comprendre l'origine des religions. Ce qu'il fera en se rendant en Egypte et en Syrie.
Puis, il se rendra aux USA en 1795 pour étudier ce pays de liberté décrit par son mentor Benjamin Franklin. Il sera même reçu avec honneur par George Washington.
Volney se rendra aussi en Corse, c'est là qu'il fera connaissance avec un certain Napoléon Bonaparte encore passablement inconnu. Plus tard il deviendra son confident. On y reviendra plus tard.
1790
Le 8 mai 1790 Talleyrand propose à l'assemblée nationale un décret pour définir une nouvelle unité de mesure universelle. Il décrit qu'il y a déjà un projet existant. Que ce serait bon pour le commerce, que Turgot y était favorable. La méthode ancienne consiste à créer des étalons et les envoyer dans toutes les villes du pays. Mais ce n'est pas une mesure universelle. Les étalons peuvent se perdre et être modifiés.
Ainsi il y a 2 idées pour créer un étalon universel:
- la première c'est de se baser sur la mesure d'un degré de méridien. "La première consisteroit à adopter pour élément de nos mesure linéaires la soixante-millième partie de la longueur du degré du méridien coupé en deux parties égales par le quarante-cinquième parallèle, & dont la la longueur a été déterminée à 57 030 toises par M. de la Caille. Cette mesure élémentaire s'est trouvée avoir 5 pieds & 8 pouces 5 lignes un quart; elle s'appelleroit un miliaire. Mille milliaires feroient un mille, trois mille feroient une lieue; & vingt lieues composeraient un degré. Le milliaire tiendroit lieu de la toise, dont il ne diffère que de 42 lignes 3 quarts, et se diviseroit comme elle en 6 parties, donc chacune représenteroit un pied."
- La seconde c'est de se baser sur la longueur d'un pendule qui bat la seconde à la latitude de 45°, soit la moyenne entre l'équateur et les pôles. (36 pouces, 8 lignes et 52 centièmes) (440,4 lignes ici) Talleyrand est favorable a cette seconde solution et propose même que le roi (encore au pouvoir) s'arrange avec les anglais pour établir un étalon commun.
13 juillet 1790
Le secrétaire d'État des USA, Thomas Jefferson propose une nouvelle unité de mesure basée sur la longueur du pendule à 45° de latitude. Il y a une coordination avec les français. La seule différence réside dans le fait que Jefferson propose un pendule avec une tige métallique et non un fil.
"Plan for Establishing Uniformity in the Coinage, Weights, and Measures of the United States"
Août 1790
Le roi Louis XVI accepte le décret proposé par Talleyrand. L'Académie des Science est mandatée pour la réforme des unités de poids et mesures.
27 octobre 1790
Une première commission composée de Borda, Coulomb, La Grange, La place, Lavoisier, Tillet et Condorcet recommande l'utilisation du système décimal pour toutes les unités de mesure. (aussi poids et monnaie)
1791
19 mars 1791 Le quart du méridien est choisi comme base de l'unité de mesure universelle. Et on oublie la collaboration internationale.
Le choix s'est fait par une commission composée de Borda, La Grange, La place, Monge et Condorcet.
(On retrouvera Gaspard Monge un peu plus tard en égypte à faire la course pour être le premier au sommet de la pyramide de Khéops...)

Bien que le 1/4 du méridien est choisi comme "l'unité réelle de mesure", tout est fait pour coller à l'autre définition rejetée de la longueur du pendule qui bat la seconde.

"Nous nous bornerons à dire ici que cette dix millionième partie du quart du méridien, qui feroit notre unité usuelle de mesure, ne différeroit du pendule simple que d’un cent quarante cinquième environ , & qu’ainsi l’une et l'autre unité conduisent à des systêmes de mefure absolument semblables dans leurs dispositions."
Justification du choix du 1/4 du méridien plutôt que du pendule
Il est étrange dans ce rapport de 12 pages d'en voir 2 qui sont consacrées au rejet de la définition du mètre par la longueur d'un pendule qui bat la seconde, mais de voir seulement 2 lignes qui adopte la proposition du quart du méridien sans qu'on y voit de réelle motivation.
Le choix semble donc ici plutôt motivé par le rejet de certaines propositions plutôt que l'adoption du 1/4 du méridien.
3 propositions de définitions sont débattues:
- la longueur du pendule qui bat la seconde
- la longueur du 1/4 du méridien
- la longueur du 1/4 de l'équateur
La définition du pendule, bien que la préférée de tous, est écartée car elle dépend d'une mesure arbitraire: la seconde !
"Cependant nous devons observer que cette unité, ainsi déterminée renferme en elle-même quelque, chose d’arbitraire. La seconde de temps est la quatre-vingt six mille quatre centième partie du jour, & par conséquent une division arbitraire de cette unité naturelle. Ainsi pour fixer l’unité de longueur, on emploie non-seulement un élément hétérogène (le temps) mais un élément arbitraire."
(Une pirouette est proposée pour conserver l'idée du pendule, c'est de concevoir un pendule hypothétique qui ne ferait qu'une oscillation par jour..... Après réflexion un tel pendule aurait la taille de la Terre à la Lune... du coup vraiment trop hypothétique pour être utilisé... )
L'idée du quart de l'équateur est rejetée car c'est trop loin de la France. De plus cet étalon ne serait pas assez universel, vu que chaque nation est sur un méridien, mais rares sont les nations sur l'équateur.
C'est ainsi que le 1/4 du méridien est choisi, car il se mesure en France.
Il est peut être utile de rappeler que des mesures à l'équateur ont déjà été réalisées 50 ans plus tôt et de l'autre côté de l'atlantique. La logistique d'une telle expédition devait donc être possible. (bien que c'était la mesure de 3° du méridien à l'équateur qui a été fait et non l'équateur lui même.)
26 mars 1791
L'assemblée nationale accepte la recommandation de la commission.
Avril 1791
L'académie des sciences confie la mesure du méridien à Méchain, Legendre et J.-D Cassini. Seul Méchain accepte.

13 septembre 1791
"Volney" (contraction de Voltaire et Ferney... un fan de Voltaire) publie un livre intitulé Les ruines, ou Méditation sur les révolutions des empires. Le 25 septembre, le volume placé sur le bureau de l'Assemblée nationale, était déposé aux archives.
L'idée première de cet ouvrage avait été conçue dans le cabinet de Benjamin Franklin. L'auteur se met en scène sur les ruines de Palmyre ; et là il se livre à de profondes méditations sur la destruction de tant d'empires à qui leur puissance colossale semblait promettre une éternelle durée, et qui n'en ont pas moins obéi à cette loi de la nature qui veut que tout périsse.

Ce livre, ainsi que le précédent, "Voyage en Syrie et en Égypte, pendant les années 1783, 1784 et 1785" (et le tome 2) publiés en 1787. (déjà mentionné plus haut) a éveillé l'intérêt du public pour l'orient et surtout pour l'égypte et ses pyramides.
Le livre "Ruines...." influence même le ministre des relations extérieures, Talleyrand qui incite le général Bonaparte à conduire la campagne d'Égypte de 1798 à 1801 !
(C'est le début de l'égyptomanie, bien que le rêve de conquête de l'égypte était déjà un projet plus ancien pour le gouvernement français. Talleyrand y pensait depuis avant la révolution, la proposition de conquête de l'égypte avait été faite à Louis XVI au début de son règne, et cette idée semble remonter à Louis XIV.)
Justement Volney est un proche de Bonaparte, ceci depuis sa rencontre avec lui en Corse.
Après le coup d'Etat du 18 brumaire qui a mis Napoléon à la tête de la France, Bonaparte imagine prendre Volney comme troisième Consul, puis comme ministre de l'Intérieur. Volney refuse, et se laissa seulement nommer sénateur, mais il reste le confident, l'ami, et même le médecin du Premier Consul.
En voyant la proximité entre Volney et les personnages influents de notre histoire, on peut imaginer ici l'influence morale et philosophique que Volney a pu avoir sur l'imaginaire des dirigeants Français qui créent un monde nouveau.
Volnay est mort en 1820, il repose au cimetière du Père-lachaise sous une pyramide !

Il existe plusieurs loges maçonniques qui portent le nom de Volney.
1792
1792 fin juin début de la Mesure du méridien entre Dunkerque et Barcelone par Méchain et Delambre. Les deux partent dans des direction opposée. Méchain pour Barcelone et Delambre pour Dunkerque. En novembre le gros de la mesure des angles est terminée jusqu'au pied des pyrénées. L'hiver est occupé à mesure les latitudes.
Le travail sera fini en 1798, si tout se passe bien pour Delambre, Méchain va réaliser 2 mesures avec des résultats différents sans en trouver l'erreur. Il va devenir dépressif, suicidaire et s'enferme dans un couvent abandonné jusqu'à ce que sa femme viennent le rechercher. Il va donc masquer cette erreur à son collègue et au public. Ce n'est qu'après sa mort que Delambre en vérifiant les carnets de Méchain va découvrir la vérité.
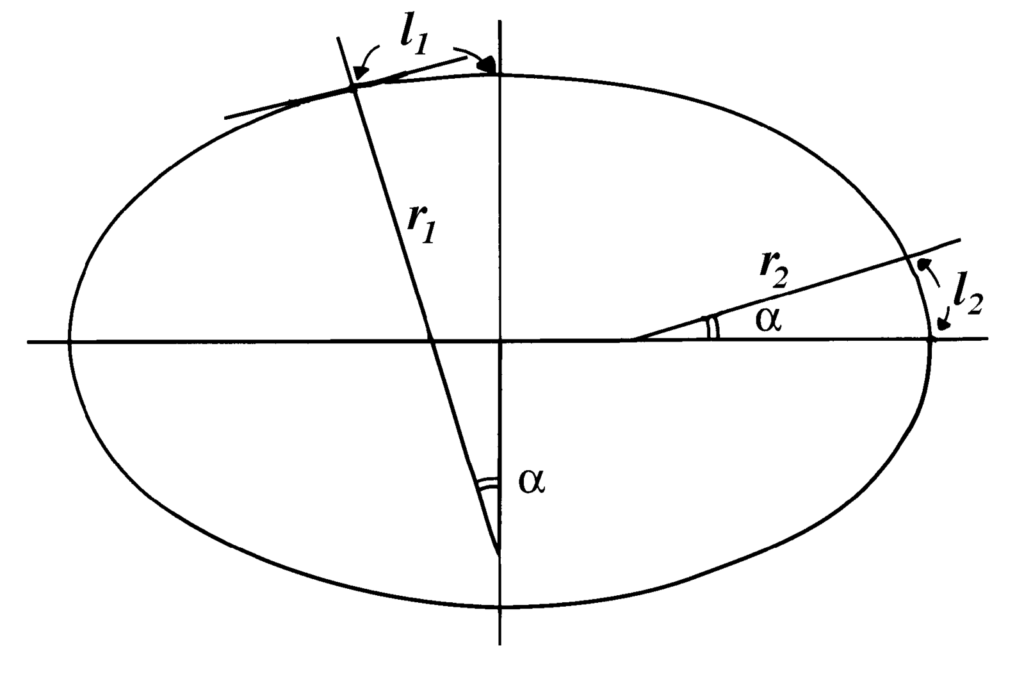
1792 Une explication est publiée par la "Commission temporaire des poids & mesures républicains" sur le pourquoi du quart du méridien. Pourquoi un quart et pas une autre proportion. Il s'agit du document "Instruction sur les mesures déduites de la grandeur de la terre : uniformes pour toute la République, et sur les calculs relatifs a leur division décimale" p.13 à 16
Le document explique que le quart du méridien est un angle droit du "cercle" (en fait une ellipse, ce que le document précise aussi.) L'angle droit est un cas particulier d'angle qui permet de mesurer facilement tous les autres et de simplifier les calculs trigonométriques. Il est mentionné que les astronomes utilisent aussi ce quart pour leur calcul. Notamment car les tables de trigonométries avec des sinus sont basées sur le 1/4 du cercle. Le reste n'étant que répétition de ce même cadran.
"(...) ce qui les y a sur-tout déterminés, c’est que tous les calculs astronomiques et autres qui ont pour élémens des mesures d’angles, se rapportent à certaines lignes tracées dans le cercle qu’on appelé sinus , et dont la série se termine au quart de la circonférence ;"

Justification de la base 10
En ce qui concerne la justification de la base 10, c'est plutôt "L'effet de l'instinct plutôt que de la réflexion", en expliquant que la plupart des civilisations dont on connait l'histoire utilisent de préférence la base 10, probablement à cause du nombre de doigts des humains !
Cette envie d'utiliser le système décimal partout va conduire à la création du grade, comme unité de mesure d'angle. L'angle droit si pratique décrit ci-dessus est associé à 100 grade. Ainsi un tour complet d'un cercle vaut 400 grade. Cette unité de mesure n'a jamais vraiment été utilisée, les degrés étant plus pratique car le nombre 360 a plus de diviseurs que le nombre 400, ce qui permet de faire correspondre des angles pratiques de la trigonométrie, comme 60° et 30°, à des nombres rond. (sin(30°) = 1/2).
Comme quoi, le même raisonnement peut valider le choix du 1/4 du méridien en mode décimal ou l'invalider pour d'autres unités.
(Il est à noter que depuis l'avènement des outils informatiques de gestion géographique, le degré décimal est souvent utilisé. Il s'agit de diviser en mode décimal les sous divisions du degré, donc la minute et la seconde sont remplacée. On a ainsi le meilleur des deux mondes )
La France est le meilleur endroit de mesure du 1/4 du méridien
Les révolutionnaires disent que sans le vouloir, le meilleur endroit pour la mesure du quart du méridien se trouve être la France, l'endroit où l'on peut mesurer une distance suffisante depuis un bord de mer jusqu'à un bord de mer et à des latitudes autour de la latitude moyenne de 45°.
Le postulat est fait que la terre est une ellipse, et donc qu'il est possible de mesurer cette valeur moyenne et d'ensuite l'extrapoler pour trouve le 1/4 du méridien. (Il s'avère que cette hypothèse de départ est fausse, la terre est un planétoïde avec des méridiens tous différents. Les savants de l'époque s'en rendrons compte grâce à l'erreur de mesure de Méchain quelques années plus tard.)
Eloge du pendule
Bien que la définition de la longueur du pendule qui bat la seconde a été rejetée. Il est précisé ici que c'est le meilleur moyen de retrouver la longueur du mètre !!
Le travail de mesure du degré de méridien ne doit être fait qu'une seul fois puis on enregistrera le nombre d'oscillations en 24h d'un pendule qui bat la seconde pour retrouver le mètre ! (sachant que la longueur du pendule est quasi de 1 mètre.. c'est étonnant d'avoir rejeté cette définition qui était proposée à l'origine dans le décret de Talleyrand pour ensuite y revenir de façon détournée !)
"Ainsi le pendule peut être regardé comme le dépositaire de l’unité de mesure , ou même comme un moyen de mesurer la terre" p.29
21 janvier 1793
Le roi Louis XVI est guillotiné.
7 mars 1793
L'espagne déclare la guerre à la France. C'est la guerre des pyrénées. Déjà que Méchain n'avait pas pu rentrer en France car il était alité depuis 6 mois suite à un accident, là on lui refuse son visa et il ne peut pas quitter l'Espagne.
Il se lance donc dans un projet de prolongement de ses mesures du méridien. Il veut atteindre l'ile de Cabrera dans la Baléares.
29 mai 1793
Une troisième commission détermine un mètre provisoire de 443,44 lignes basé sur les mesures faites en 1740 par Lacaille et Cassini de Thury.
Ce mètre provisoire est adopté dans un décrêt du 1er août.
21 décembre 1794
Il pousse la précision en utilisant 2 étoiles de plus que lors de ses mesures précédentes. En plus de l'inclinaison de la Terre, il obtient en bonus, la validation de ses résultats de mesures de la latitude à Montjuïc issue de la mesure de la hauteur de 6 étoiles : Polaris, Kokab, Thuban, Mizar, El Nef et Pollux.
Tout se passe bien avec les premières mesure. La localisation du château de Montjuïc se fait à 30 pieds près.
Mais, voilà que le résultat lié à Mizar donne une erreur de 4 secondes d'arc, soit ~400 pieds. C'est le drame !
Il passe 3 mois à refaire les mesures et calcul, puis après de longue négociation obtient le droit de faire une mesure depuis le château de Monjuïc (en pleine guerre), le dimanche 16 mars 1794.
Impossible de trouver la source de cette incohérence. Méchain devient dépressif. Il a déjà communiqué ses premières données. Il commence à masquer le fait qu'il existe une erreur.

7 avril 1795
Le système métrique décimal complet (sauf la seconde) est adopté dans la loi.
10 juillet 1796
Gaspard Monge écrit à sa femme.
Bologne, le 22 messidor de l'an IV de la République
Nous avons encore à faire ici [Bologne] pour trois ou quatre jours ; nous sommes fort occupés de nos emballages qui contiennent des objets très précieux en tout genre. Indépendamment des beaux tableaux de Bologne, nous envoyons à Paris une donation manuscrite faite à l'église de Ravenne, sur papyrus en l'an 490, c'est-à-dire il y a 1306 ans,[beaucoup de manuscrits anciens et de premières éditions imprimées.] Je crois que la Bibliothèque nationale sera très contente de notre envoi.
Nos affaires terminées ici, nous nous rendrons à Florence où nous serons sans fonction et où nous attendrons que notre ambassadeur à Rome nous avertisse qu'il est temps de nous rendre dans cette capitale du monde chrétien. Je crois que nous y serons dans une quinzaine de jours.

17 août 1796
Gaspard Monge écrit à son gendre
Rome, le 30 thermidor de l'an IV de la République
Mais l'abbaye de San Salvator à Bologne a une grande bibliothèque que personne ne fréquente, et dont les moines eux-mêmes ne connaissent que la porte. Nous y avons trouvé 120 volumes imprimés avant l'année l500, et environ 500 manuscrits antérieurs à l'époque de l'invention de l'imprimerie, et nous avons pris tout cela parce que cela sera utile à Paris, et que cela ne l'était plus depuis bien longtemps à Bologne.
Nous avons trouvé aussi à Bologne trois donations faites en 490 et 491 à l'église de Ravenne, écrites sur papyrus ; nous les avons prises; et, depuis que nous sommes ici, nous avons reconnu que la fameuse Chambre des papyrus du Vatican ne renferme qu'une douzaine de semblables donations et rien d'autre. Ainsi les papyrus que nous avons eus de Bologne, le livre de Joseph que nous avons eu à Milan et quelques-unes des donations du Vatican que nous emporterons, rendront la bibliothèque de Paris plus riche en ce genre que l'on ne l'est à Rome, sans compter ce qu'elle avait déjà en ce genre et qui était très considérable.
23 août 1796
Lettre de Gaspard Monge à sa femme
Rome, le 6 fructidor de l'an IV de la République
Nous sommes toujours occupés à former notre liste de manuscrits. Rien ne presse à cet égard, parce que quand un convoi sera prêt à partir, nous donnerons cette liste et en trois jours les ballots seront faits pour être chargés sur les voitures. Si le catalogue de la Bibliothèque du Vatican existait, il suffirait de le compulser. Mais il n'existe que celui des livres hébreux et celui des livres syriaques. Ces jours derniers, nous avons visité tous les livres arabes et nous avons eu soin de ne marquer que ceux qui ne sont pas dans la Bibliothèque de Paris.
Il s'en faut de beaucoup que nous connaissions la Bibliothèque du Vatican, mais à en juger par ce qui nous est déjà passé par les mains, je t'assure que sa célébrité tomberait considérablement si le catalogue en était fait. Elle ne renferme que des manuscrits et lorsque nous l'aurons écrémée en envoyant à Paris tous les objets célèbres et connus de réputation, je t'assure qu'il sera encore plus nécessaire que jamais de tenir ce catalogue secret.

3 juin 1797
Gaspard Monge écrit à sa femme
Rome, le 15 prairial de l'an V de la République
L'autre jour, après avoir mis à part dans la bibliothèque du Vatican quelques manuscrits anciens relatifs à l'histoire, et qui ne pouvaient avoir quelque mérite que dans le cas où ils n'auraient pas été imprimés, j'allai, avec l'abbé qui travaille avec moi, à la bibliothèque de la Minerve pour voir s'ils étaient publiés. Après avoir parcouru les catalogues, il nous restait à vérifier quelque chose dans quelques ouvrages au nombre desquels se trouvaient les œuvres de Galilée, célèbre Florentin qui s'avisa de découvrir que la Terre tournait, qui eut la bonhomie de le dire, qui fut emprisonné pour cela, et qui fut obligé de se rétracter pour avoir la liberté, ce qui, comme il le dit lui-même, n'empêcherait pas la Terre de tourner.
Le bibliothécaire, Jacobin de religion, en nous apportant la charge de livres que nous avions demandés, et en nous montrant les volumes de Galilée, nous dit ceux-ci sont défendus. Mon abbé, homme d'esprit, très honnête et qui vraisemblablement n'était pas comme lui, dit "J'ai la permission de lire tous les livres, quant à Mr, en me montrant, il l'a par lui-même". Cette assertion donnée de preuve ne faisait pas grand effet sur le suppôt de l'inquisition qui prétendait qu'il fallait aller parler au supérieur; mais en tournant mon chapeau de manière à rendre visible ma cocarde, je levai toute difficulté ; et, après avoir jeté un coup d'œil expressif à mon pauvre abbé, nous fîmes notre opération.
Pendant que nous nous en occupions, un jeune homme vint se placer à côté de nous, et un moment après on vint lui apporter les livres qu'il avait demandés. Je fus surpris de voir que c'était l'Astronomie de Lalande 1° parce que les sciences positives ne font pas grande fortune à Rome ; 2° parce que l'on ne défend pas le livre de Lalande qu'on lit tous les jours et qui suppose d'un bout à l'autre que la Terre tourne, tandis qu'on défend encore les livres du pauvre Galilée que personne ne lit plus. Mais dans le régime de l'erreur, il faut avoir bien de l'esprit pour être conséquent et pour faire tout cadrer; et depuis bien longtemps il n'y en a plus guère dans ce pays-ci ; et je crois, dieu me pardonne que, sans nos élégantes et nos incroyables, la farce finirait bientôt.
1798
L'expédition de mesure du Méridien est terminée.

19 mai 1798
Les soldats et 167 scientifiques de la campagne d'égypte quittent le port de Toulon avec Napoléon pour se rendre en Egypte où ils arriverons en juillet.
C'est Gaspard Monge qui a sélectionné en secret pendant les 2 mois précédents au moins 150 des scientifiques présents. Avec Napoléon et ses généraux, c'est le seul membre de l'expédition à connaitre la véritable destination.
Parmis les scientifiques embarqués, il y a l'astronome Jérôme Méchain. Le fils de l'astronome Pierre Méchain qui mesure le méridien jusqu'à Barcelone.
J'ai découvert ceci lors de ma visite au temple de Philae en égypte, sur un des murs il était gravé "Méchain". Ça m'a questionné.
Il est rentré en octobre 1801, plus tôt que les autres, suite à une négociation avec les anglais, et pour pouvoir ramener les résultats des travaux scientifiques menés.

Au passage, vu que l'on parle de la famille Méchain, je profite de l'occasion pour dire que cette famille vient de Laon. Ville où ironiquement, la cathédrale contient une pierre angulaire qui marque le mètre.... Pourquoi aller si loin quand on a tout chez soi !
1799
La fixation provisoire de la longueur du mètre du 1er août 1793 (18 germinal 3) est révoquée et la version définitive est adoptée le 19 frimaire an 8 (10 décembre 1799).
Elle vaut 3 pieds 11 lignes 296/1000. (443,296 lignes)
Delambre propose d'arrondir à 443,3 lignes, mais la commission veut exploiter pleinement la précision proposée par l'ingénieur Étienne Lenoir qui réalise l'étalon.
Le 22 juin, le mètre standard sous forme d'étalon en platine est officiellement présenté.
La loi du 19 Frimaire, an VIII (10 décembre 1799) précise : « le mètre et le kilogramme en platine déposés le 4 Messidor dernier au Corps législatif par l'Institut national des Sciences et des Arts sont les étalons définitifs des mesures de longueur et de poids dans toute la République… ».
Ce mètre-étalon, connu aujourd'hui sous le nom de Mètre des Archives. Il sera LA référence officielle jusqu'en 1889.
On sait que par rapport à la mesure réelle du 1/4 du méridien cette version définitive du mètre est trop courte de 0,197 mm. (Ce qui fait que le méridien fait 40 007, 864 km au lieu de 40 000 km tout rond.) Mais cette erreur se perpétue de définition en définition.
Autre erreur de taille, le fondement même de la méthode ne fonctionne pas !
L'idée de mesurer un segement de méridien (celui entre Dunkerque et Barcelone) afin d'extrapoler la mesure pour déterminer la distance du quart du méridien ne fonctionne pas, car la Terre n'est PAS une ellipsoïde de révolution, mais un planétoïde où tous les méridiens sont différents.
(regarde une orange ou une pomme.. généralement elle est pas parfaite.)
Les savants qui ont mis a point cette méthode de mesure ont pris pour hypothèse que la Terre est une ellipsoïde de révolution. Mais ils ont bien précisés que c'est une hypothèse.
Déjà à ce moment là, le taux d'aplatissement a du être mesuré. C'est ainsi que pour déterminer le mètre définitif, les données de l'expédition géodésiques françaises à l'équateur et en Laponie ont été utilisées pour déterminer l'aplatissement de la Terre.
Un aplatissement de 1/334 a été choisi en combinant l'arc du Pérou mesuré par La Condamine et les données de la méridienne de Delambre et Méchain, avec pour point central le panthéon à Paris.
Donc on se retrouve avec un calcul hybride, la commission se retrouvant avec 2 aplatissements possibles 1/150 mesuré par Méchain et Delambre et 1/334 mesuré par La Condamine !! .. donc ne comprenant pas trop la mesure de Méchain et Delambre seul leur longueur a été retenue, mais pas leur aplatissement !! (cohérent tout ça !!!)
De nos jours le système WGS84 utilise un aplatissement de 1/298.257223563.
Donc de là, il faut bien comprendre que chaque méridien est est unique. La Terre est un géoïde et pas une forme régulière... il suffit de regarder une orange pour avoir une bonne analogie !

Donc les gars ont dit qu'ils avaient vraiment mesuré la Terre et de façon très précise. Mais la réalité, c'est que Méchain avait fait une erreur due à l'usure de son cercle répétiteur de Borda. Donc une cohérence à chaque mesure, mais une différence si on refait la mesure plus tard avec une autre usure ! L'axe vertical étant altéré. C'est l'astronome Jean-Nicolas Nicollet qui a élucidé l'erreur en 1828. Il a pu la corrigé grâce nombreuses mesures faites par Méchain au nord et au sud du zénith, permettant de se compenser.
Méchain avait choisi une des deux valeurs, et malheureusement la moins précise. Delambre trouvait que tout ce travail était inutile pour juste déterminer un étalon, mais il a bien aimé faire le travail. Du coup il a proposé une précision moindre, avec un nombre simple de ligne à retenir 443,3 ... 2* 4 et 2 * 3.... mais la commission voulait briller en montrant une précision... (absurde)....
Puis il y a ce mélange de 2 sources de mesures, une pour la distance et une pour l'aplatissement !
De là on extrapole, de 9.5° pour 90° .... alors qu'on soupçonne que l'extrapolation est un non sens vu que la Terre n'est pas une ellipsoïde, mais un géoïde irrégulier avec des méridien tous uniques !
Le coup de la mesure universelle en prend un coup.... c'est donc un mètre français !!
Et de là on voit que la fable de la précision est une fable... et pas la réalité.
Je me questionnait de savoir si le mètre n'aurait pas été repris d'ailleurs vu les difficultés de réaliser une telle mesure. Mais je crois bien que non. Nous utilisons bien ce mètre imparfait de ~2 dixième de mm .... ce qui ne change pas grand chose !
1804
Méchain meurt de la malaria à Barcelone en essayant de vérifier ses mesures.
Delambre fait l'éloge de son collègue Méchain dans les mémoires de l'académie des sciences en 1805.
1806
L'erreur de Méchain
Delambre récupère les carnets de notes de Méchain. On sait par les recherches récentes de Ken Alder que Delambre avait découvert l'histoire de l'"erreur" de calcul de latitude faites par Méchain. Méchain a tenté de masquer ses mesures incohérentes, mais n'a jamais trouvé l'explication. Ça l'a rendu malade et on peu même le dire, ça l'a tué..
On retrouve l'explication dans un livre de Ken Alder qui s'appelle "Mesurer le monde".
Delambre a écrit dans le carnet de Méchain qu'il a choisi une des deux versions de la mesure, mais qu'il n'en informerai pas le public, car il n'a pas besoin de le savoir.
La pensée la derrière est que le système métrique doit s'imposer et il ne faut pas ajouter de flou, au risque de voir ce système remis en cause. Il vaut mieux une bonne histoire qui raconte une merveilleuse expédition scientifique pleine de rebondissement, mais que malgré tout l'effort de la brillante communauté scientifique française a réussi à mesurer le 1/4 du méridien et en tirer une unité de mesure universelle pour le bien de l'harmonie des peuples... Bref.. l'histoire qu'on nous raconte toujours et dont on a fait des films.
En fait quand Méchain cherchait l'erreur dans ses mesures des étoiles. Delambre a vu là une remise en cause du postulat que la Terre est une ellipsoïde, mais que c'est une géoïde. Donc cette erreur, n'en est pas une. C'est une remise en question du modèle théorique et donc une occasion de grandir d'aller vers un meilleur modèle.
La vérité était encore ailleurs. En 1828, Jean-Nicolas Nicollet découvrira que c'est l'usure du cercle répétiteur de Borda qui est la cause d'une déviation constante de l'axe du zénith. Il le prouvera en compensant les déviations relevées par Méchain au nord et au sud. On découvre ainsi que Méchain avait une précision redoutable de 40 pieds pour la mesure de la latitude. Mais sa méthode de calcul ne distiguait pas la précision de l'exactitude.
Ken Alder dans son livre "Mesurer le Monde" insiste sur les bénéfices de cette "erreur" qui n'en est pas une et qui fera évoluer les méthodes de mesures et la statistique, grâce aux mathématiciens Legendre et Gauss qui ont découvert simultanément la méthode des moindres carrés. On peut ainsi distinguer précision et exactitude grâce à un modèle théorique.
Une ancienne civilisation connaissait déjà le mètre ?
Une fois tout ses travaux terminé Delambre publie une livre qui résume la mesure du méridien et la création du mètre:
Dans ce livre il fait l'état des lieux des connaissances et on a des phrases étranges. Il cite Paucton et remet en cause ses calculs grâces aux mesures de la pyramide faites pendant la campagnes d'égypte.

Delambre semble au courant de l'hypothèse que le mètre était déjà utilisé par une ancienne civilisation avant son invention officielle !
Mais pour lui, il se fiche bien de l'origine du mètre. Tant que cette unité de mesure existe et est utilisée.

1809
Publication de la première édition de "Description de l'égypte", avec le compte rendu scientifique de la campgne d'égypte. Cette édition est dirigée par Edmée Jomard.
1817
Edmée Jomard publie son livre "Mémoire sur le système métrique des anciens égyptiens: contenant des recherches sur leurs connoissances géométriques et sur les mesures des autres peuples de l'antiquité " publiée en 1817...... "

La citation de M. Gosselin mise en avant est intéressante, car il y est dit des vérités qui semblent oubliées de nos jours:
"On se convaincra, d'après ces recherches, que les mesures itinétaires des anciens sont plus exactes qu'on ne le croit. En les comparant au plan de la terre, tel qu'il nous est connu, il est souvent difficile, quelques fois même impossible, de décider si les erreurs que l'on croit apercevoir dans ces itinérairess, doivent être rejetées plutôt sur le compte des anciens que sur l'imperfection de nos connoissances actuelles."
Recherches sur la géographie systématiques et positive des anciens, par M. Gossellin,
Jomard explique directement dans le début de son livre, que l'orient et particulièrement l'égypte a attiré tous les gens intéressés par la recherche d'une unité de mesure naturelle.
C'est en effet, ce que l'on constate ici, avec les exemples du calife Al-Mamoun, de Graves, de Burratini, de Newton et de Paucton. Certains sont allés sur place et d'autres non. Jomard précise qu'il a de la chance d'être sur place et avec du bon matériel de mesure. Il n'est pas ainsi obligé de se fier aux estimations des mesures des voyageurs.

Le périmètre de la pyramide de Khéops est ajusté sur la longueur du méridien
p284:
"Mais le périmètre de la grande pyramide de Memphis avoit 30 secondes du degré propre à l''Egypte, autrement cinq stades compris chacun 600 fois dans ce même degré: l'apothème avoit un stade; le côté, 500."
"Ainsi le côté de la pyramide répété 480 fois, ou le périmètre pris 120 fois, faisoit le degré terrestre. Multiplié 8 fois, ce même côté faisoit une minute. La mesure d'une seconde étoit conservée dans la 30è partie du périmètre. Le schoene, grande mesure itinéaire, 10è partie du degré, étoit égal à 48 fois le côté de la pyramide, ou 12 fois son périmètre, etc, etc,"
J'ai vérifié, ça marche très bien. La longueur du degré du méridien propre à l'égypte (30° de latitude) mesure 110852.4248 m. Si on divise cette longueur par 120 on obtient 923.8m pour le périmètre de la pyramide, soit 230.942 m pour un côté. Ce qui à une coudée près correspond aux 440 coudées officiellement admises. (mais avec de grandes variations suivants les auteurs !) La différence s'explique probablement à savoir si l'on prend en compte le socle de la pyramide où non !
1821
Publication de la seconde édition de "Description d'Egypte".
Il est donc naturel de penser que l'étude des monnumens laissés par les Égyptiens y fera retrouver leur système métrique: c'est là la fin essentielle de notre travail, notre but n'étant pas de donner un tableau de toutes les mesures appartenant aux divers peuples et cités par les auteurs.
Outre que cette recherche serait hors du plan de l'ouvrage et au-dessus de nos forces, elle se trouvera faite en partie, pour ainsi dire, par la seule détermination des mesures égyptiennes. Celles-ci, en effet ont donné naissance à beaucoup d'autres, telles, par exemple, les mesures hébraïque, ainsi que l'atteste positivement S. Épiphane.
Que veut vraiment dire Jomard par ces propos ?
Est-ce qu'il dit réellement que son mandat, la "fin essentielle de notre travail" est de retrouver "le systèmes métrique" des anciens Égyptiens ?
Où est ce qu'il s'est donné lui même cette mission d'étudier le système de mesure des anciens égyptiens ?
La suite de la saga du mètre au prochain épisode !
Maintenant que nous avons les faits et la chronologie, il sera temps de relier tout ça, d'y mettre de l'ordre et d'y retrouver un sens !
Les lecteurs attentifs pourrons déjà y voir les indices que j'ai laissé dans cette chronologie de l'invention du mètre.
A bientôt, garde l'esprit ouvert !
🝆
Voir aussi
Voici d'autres chronologies et documents intéressants à propos de l'histoire du mètre et par corollaire, de l'histoire de la mesure de la Terre.
- histoire de la définition des unités...
- histoire de ldivision décimale...
- la page wikipedia sur le mètre...
- la page wikipedia histoire du mètre...
- la page wikipedia: Figure de la Terre et histoire du mètre
- la page wikipedia: Figure de la Terre et méridienne de Delambre et Méchain
- Publication scientifique: Les origines du système métrique en France et la Convention du mètre de 1875, qui a ouvert la voie au Système international d'unités et à sa révision de 2018
- Publication scientifique: Why does the meter beat the second?
- Une liste d'unités de mesures et leur origine...
- Une chronologie des mesures de la circonférence (ou rayon) de la Terre.
- Conférence de Ken Alder sur l'erreur de Méchain durant la mesure du méridien.
- Vidéo de la conférence de Ken Alder sur l'erreur de Méchain
- Le livre de Ken Alder qui s'appelle "Mesurer le monde".
- Article du Point qui mentionne le livre de Ken Alder
- Une liste d'étalons de mesures retrouvés
- La définition du mètre de 1983
- La définition du mètre de 1960
- La définition du mètre de 2019. Voir aussi sur wikipedia
- Mon calculateur de longueur de degré de méridien.
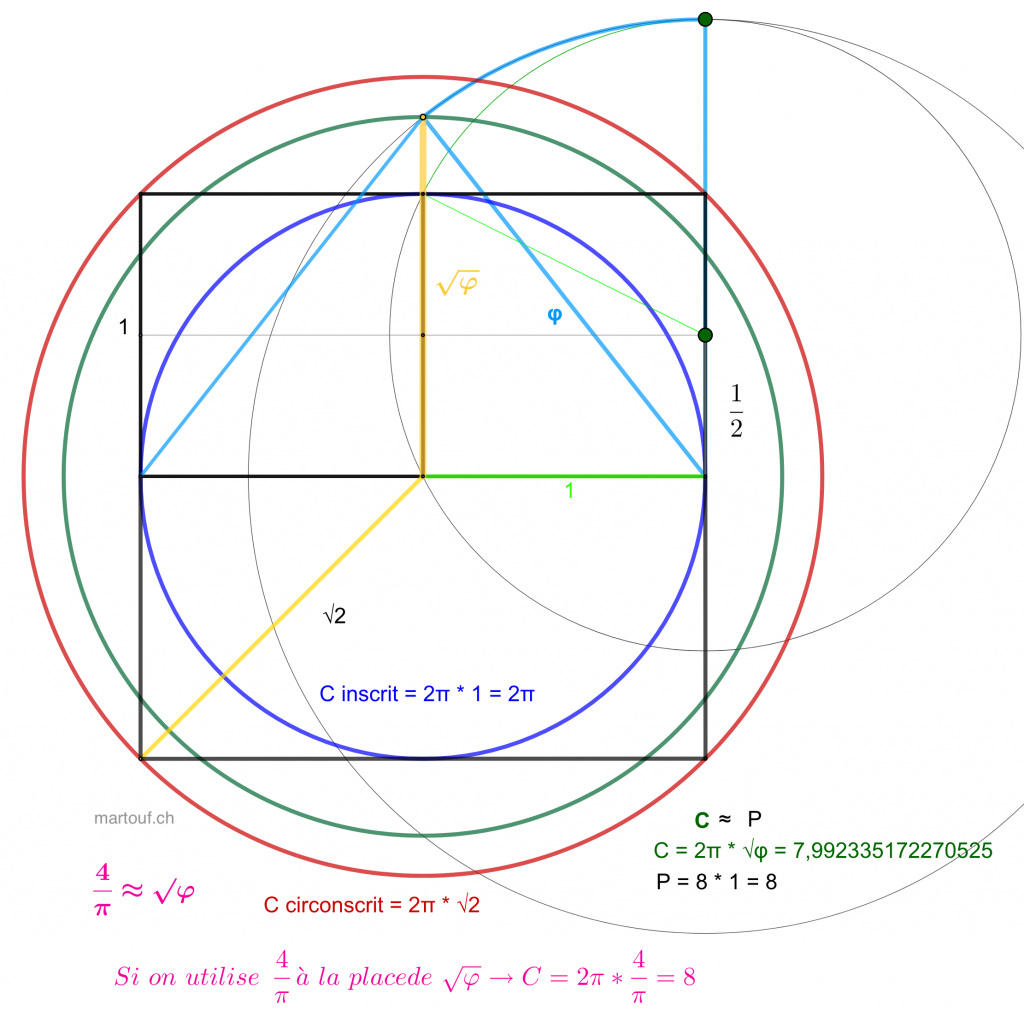
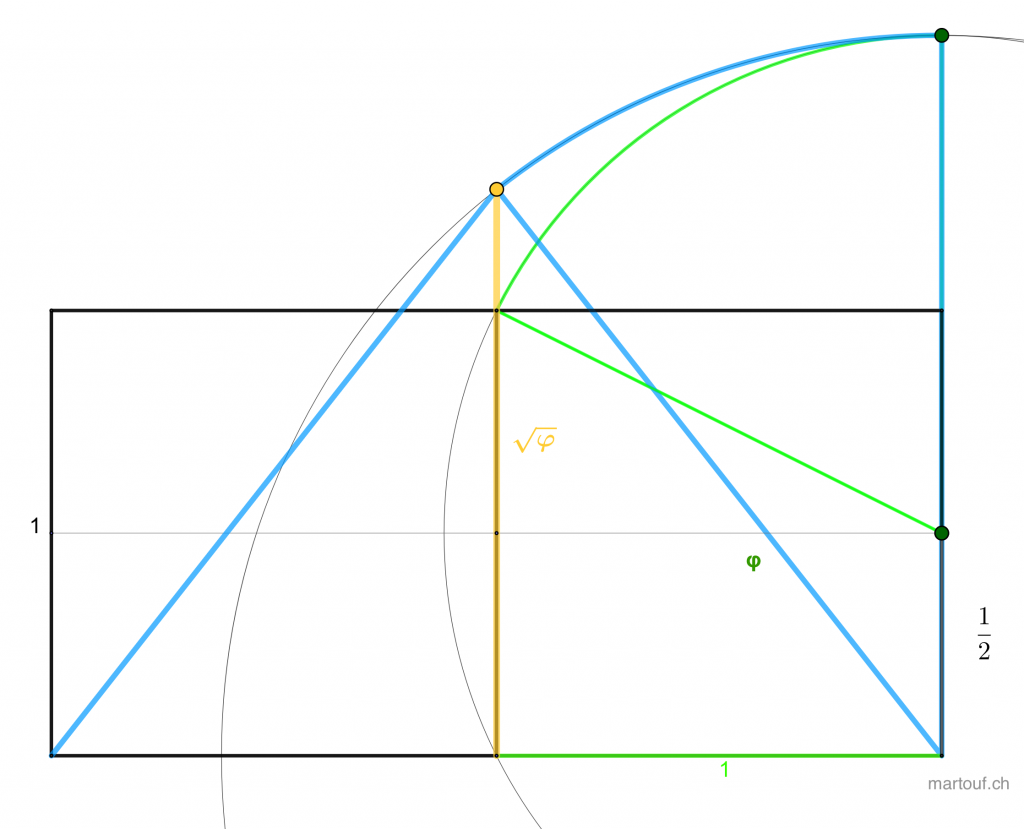
- Magazine Wired: What does pi have to do with gravity ?
- le pendule, le mètre et la seconde....