mégalithe Archives - Martouf le Synthéticien

Qu’est ce que la géométrie sacrée ? – Introduction

La plupart des gens ont fait de la "géométrie" à l'école, mais qu'est-ce que la "géométrie sacrée" ?

La langue des oiseaux nous donne directement une réponse: la géométrie: Ça crée.

Bien qu'incomplète, je trouve que c'est une bonne définition. Car oui, la géométrie permet de créer.

C'est même la base de l'art des bâtisseurs, et pas n'importe lesquels. On parle là des bâtisseurs des monuments les plus connus, les plus emblématiques, les plus beaux, et aussi les plus mystérieux de cette planète!

En effet, la géométrie sacrée est omniprésente chez les bâtisseurs de cathédrales, mais aussi chez les bâtisseurs de pyramides et même chez les bâtisseurs de mégalithes.

La géométrie sacrée est probablement une des sciences les plus anciennes qui existe.

Dans cet article nous allons voir les bases de la géométrie sacrée, nous allons voir de quoi te faire l'oeil à une autre manière de voir.

Ainsi tu pourras regarder sous un oeil neuf des monuments que tu as déjà certainement vus, mais dont tu n'avais pas pris l'ampleur de la magie de leur construction !

Introduction à la Géométrie sacrée en vidéo

Le contenu de cet article est également disponible en vidéo. Les contenus se recoupent, mais parfois il y a des anecdotes que l'on ne voit quand dans une seule version.

Tout est question de proportion

Pour bien entrer dans le sujet de la géométrie sacrée. Il faut se remettre dans le contexte ancien. Le mode de pensée n'est pas le même que de nos jours.

La manière d'aborder les mathématiques dans l'antiquité et de nos jours est très différente.

De nos jours on aime bien utiliser les nombres à virgule.

Si je prend un passant au hasard dans la rue et que je lui demande ce qu'est le nombre PI, π....

..... majoritairement il va me répondre:

C'est 3,1415.....

OK, c'est juste, c'est la représentation du nombre π sous forme de nombre à virgule. Mais quel est le sens du nombre π ? Qu'est-ce qu'il représente ?

Si la personne a fait un peu quelques études, elle va me répondre qu'il y a un lien avec le cercle.... mais la réponse complète est rare.

Alors pour te "culturer" un peu, le nombre π représente le rapport qu'il y a entre la circonférence d'un cercle et son diamètre. Ce rapport est toujours le même peu importe la taille du cercle. On a donc là une proportion, juste une proportion peu importe la taille, la mesure de l'objet.

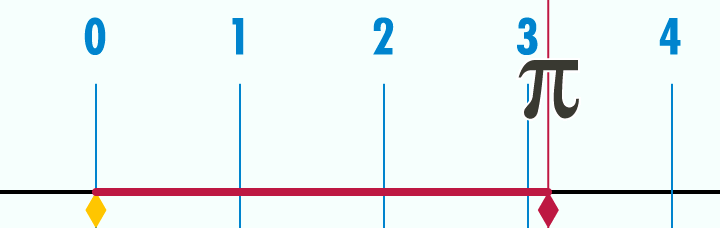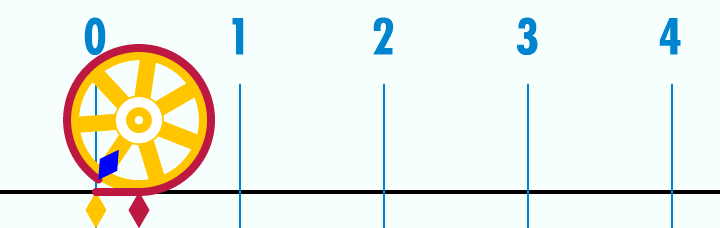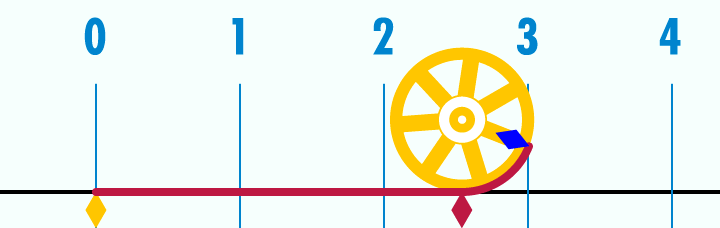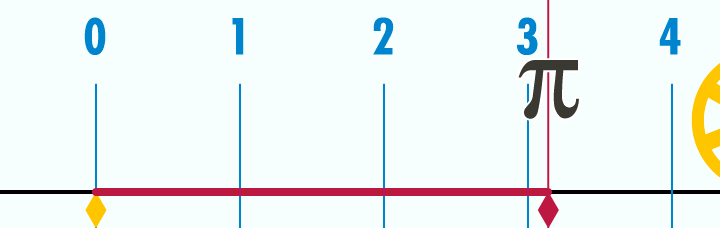
Animation qui montre le rapport entre la circonférence et le diamètre d'une roue soit π

Ainsi, cet exemple montre bien qu'il est possible de manipuler des objets mathématiques juste avec des proportions.

C'est plus tard, dans un second temps que l'on va fixer la proportion à une échelle précise en se basant sur une grandeur physique réelle.

La taille de la Terre par exemple... d'où le fait que l'on parle de Geo-métrie, mot qui signifie mesure de la Terre.

On verra plus tard, que les unités de mesures utilisées en géométrie sacrée sont tout à fait étonnantes.... On va parler de pieds, de coudées, mais aussi du mètre.

Là on verra que l'histoire officielle ne semble pas correspondre avec l'observation des monuments anciens !!

Il y a un bug dans la matrice !!!

Une des explications possible, est que des sociétés secrètes ne nous ont pas tout dit.... Je pense particulièrement à des sociétés qui ont un compas et une équerre comme emblème.....

Des sociétés chez qui la Géométrie semble quelques chose d'important, et même de sacré...

Sans calculatrice il est possible d'être plus précis

Tu peux également abandonner ta calculatrice, car en géométrie sacrée, on se fiche bien de savoir que π se représente en notation décimale à virgule par 3,1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679821480865132823066470938446095505822317253594081284811.... et encore des milliards de décimales...

Cette représentation est très lourde, toujours incomplète et donc jamais exacte. Alors qu'il suffit d'une lettre pour tout dire: π

En géométrie sacrée, il faut penser comme les anciens. Si l'on se met dans ce mode de pensée, il y a des correspondances qui sautent aux yeux, alors que si on reste dans le mode notation décimale à virgule, on passe à côté.

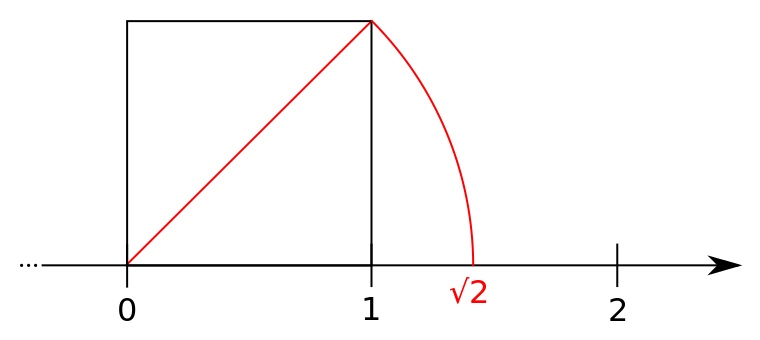
Voici encore un exemple d'un sondage dans la rue. Si je prends quelqu'un au hasard et que je lui demande ce qu'est la racine carré de 2, soit la notation: √2 .....

.... et bien là j'ai souvent un grand silence. Ou encore, la personne sort son smartphone 📱et tente de trouver le symbole √ sur sa calculette... et c'est le drame... sauf si elle connait l'astuce de passer son iPhone en mode panoramique pour découvrir des touches supplémentaires...

... et là on me dit fièrement √2 = 1.414213562373095048801688724209...

OK, mais comme avec le nombre π ci-dessus, je demande: ... et ça représente quoi √2 , ça a quel sens ?

Bref, tu l'auras compris. Notre société ne fonctionne pas du tout de la même manière. On a un certain savoir de type bourrage de crâne, mais quand à comprendre le fondement des choses. C'est pas terrible.

Donc, la racine de 2 peut tout simplement se comprendre comme étant la diagonale d'un carré de 1 de côté. (toujours en proportion, sans échelle particulière)

racine-de-2-diagonale-carre-Construction_of_square_root_of_2_on_the_line_number — La racine carrée de 2 est tout simplement la diagonale d'un carré de 1 de côté.

On verra ci-dessous, qu'en géométrie sacrée, les diagonales de carrés et de rectangles sont très souvent utilisées. Notamment pour représenter la notion d'angle.

La plus ancienne représentation que l'on a de la connaissance mathématique de la racine carrée de 2 date de ~ -1900. Il s'agit de la tablette d'argile YBC 7289.

Tablette d'argile babylonienne YBC 7289 montrant la √2 — Tablette d'argile babylonienne montrant la √2

Personnellement, depuis que je m'intéresse à la géométrie sacrée, je vois des constructions, notamment mégalithiques, qui mettent en oeuvre des connaissances mathématiques du même type et ceci dans un temps bien plus ancien !

Depuis quelques années, Norman Wildberger, un Dr en math, professeur dans une université australienne développe une nouvelle forme de trigonométrie dite rationnelle, la trigonométrie de Wildberger.

Cette trigonométrie est beaucoup plus simple à utiliser et plus efficace pour faire des calculs par ordinateur car elle ne manipule pas de nombres réels à virgule flottante. On retrouve donc là une approche similaire à celle des anciens. Et on se dit que c'était très intelligent !!

On redécouvre de plus en plus, que notre mode de pensée actuel nous fait passer à côté d'autre chose. On redécouvre que cette ancienne manière de penser qu'on voit souvent comme primitive est en fait souvent plus évoluée qu'on le crois au premier abord.... et même plus évolué que ce qu'on fait actuellement !

Plein de nombres constructibles irrationnels et même transcendants!

Alors que de nos jours on aime bien utiliser des nombres un peu ronds.... 1 mètre, 2 mètres. ou encore, 1,5m ou à la limite 2,60 ou 3,9.... les anciens ont l'art d'utiliser des nombres spéciaux qui sont difficilement représentables avec la notation décimale à virgule.

Donc c'est normal qu'on ai un peu de peine à se comprendre !

🤷🏼‍♀️

Des nombres constructibles

On a déjà vu ci-dessus des nombres comme π ou √2. Mais on verra que c'est pas fini. Il y a encore une foule d'autres racines... notamment √3 et √5. Ceci tout simplement car c'est ainsi qu'on calcule la diagonale d'un rectangle. (ci-dessous représentée par la lettre c)

On utilise le fameux théorème de Pythagore. (en fait ce théorème était connu bien avant la naissance de Pythagore... ce dernier l'a juste rapporté comme souvenir d'un voyage en égypte...)

\[c = {\sqrt{a^2+b^2} }\]

Les nombres √2, mais aussi √3, sont des nombres dit irrationnels, car on ne peut pas les exprimer par un ratio. (une fraction simple)

Mais comme on l'a vu par la géométrie, ce sont des diagonales. C'est simple à manipuler. Ce sont des nombres dit Constructibles. Car on peut les construire à la règle et au compas.

Des nombres non constructibles à la règle et au compas

Par contre pour le nombre π, c'est aussi un nombre irrationnel, mais en plus il est transcendant !
(comme son copain le nombre e)

Ça signifie que π n'est la solution d'aucune équation polynomiale. Donc avec ça on est coincé. Il n'est pas possible de dessiner le nombre π.
(Donc sur une ligne droite, sans le dérouler comme c'est fait dans l'animation en début de page.)

Pour dessiner π il y a des méthodes d'approximation, mais ça reste une approximation. C'est la cas par exemple de la méthode de Kochanski.

Le problème de la non-constructibilité de π, c'est ce qui empêche de résoudre le problème de la quadrature du cercle. Un problème qui a occupé les mathématiciens pendant des millénaires.

L'idée de base c'est de construire un carré qui a la même aire (surface) qu'un cercle donné.

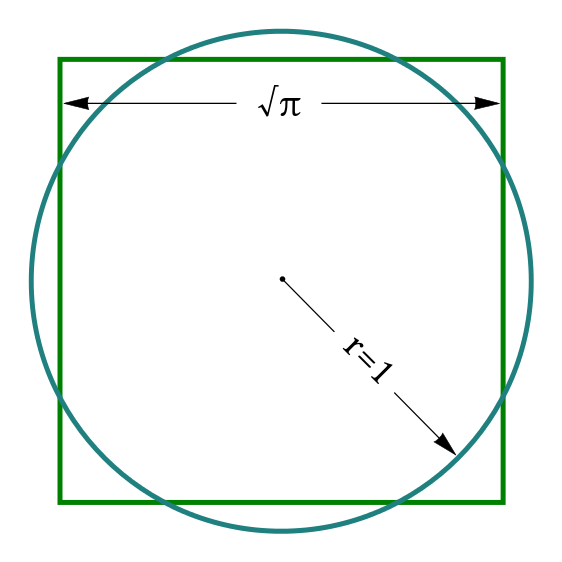
quadrature du cercle Le carré de côté √π a la même surface que le cercle de rayon 1 — Le carré de côté √π a la même surface que le cercle de rayon 1

Pour construire ce carré, il nous faut trouver la √π .... et là ça coince. Impossible à résoudre avec seulement un compas et une règle.

Donc depuis la fin du 19ème siècle on sait que c'est peine perdue de trouve une solution à ce problème, à cause de la transcendance de π.

D'où l'expression "Chercher à résoudre la quadrature du cercle"...

.... et pourtant !

La grande pyramide de Gizeh une solution au problème de la quadrature du cercle.

De mon observation de la géométrie sacrée et des monuments anciens, je vois que le problème de la quadrature du cercle a été résolu. Du moins, ça en est une excellente approximation.

Cette solution c'est la grande pyramide de Gizeh. La géométrie de cette pyramide nous montre une base carré qui a pour origine un cercle qui sert à construire la hauteur de la pyramide.

On reviendra sur la géométrie de la grande pyramide dans un article dédié car c'est là l'emblème même de la géométrie sacrée. Il y a tellement de chose à dire sur ce monument incroyable !

Le nombre d'or, le cœur de la géométrie sacrée

Ici j'aimerai juste souligner que cette prouesse d'avoir matérialisé en si imposant la solution de la quadrature du cercle tient aux propriétés d'un nombre que je n'ai pas encore évoqué ici, mais qui est le cœur de la géométrie sacrée. Il s'agit du nombre d'or.

On l'écrit avec la lettre phi: φ

Il y a tellement de choses à dire sur le nombre d'or, ou plutôt la proportion dorée, vu qu'on a dit que tout est proportion, que j'avais déjà écrit un article pour montrer tous les domaines dans lesquels le nombre d'or est la structure sous-jacente.

On a de la chance, le nombre d'or est un nombre constructible. Il vaut:

\[φ = {1 + \sqrt{5} \over 2} ≈ 1.61803398875\]

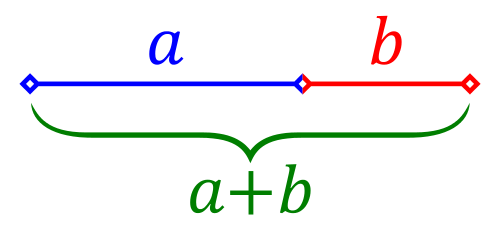
Trois points alignés, déterminant deux segments forment une section dorée (un rapport égal à Phi), s’il y a de la petite partie à la grande, le même rapport que de la grande au tout.

\[{a+b \over a} = {a \over b} \]

Le nombre d’or est le seul rapport qui met en résonance la partie avec le tout. On peut donc le voir comme étant une résonance (fractale) entre la créature et son créateur.

C’est pour cette raison que ce rapport est souvent appelé: La divine proportion.

Dans le cas de la quadrature du cercle, l'astuce utilisée dans la construction de la grande pyramide de Gizeh a été de remplacer un expression de π inconstructible par une expression approximative de composée de φ qui elle est constructible:

\[{4 \over π} ≈ {\sqrt{φ}} \]

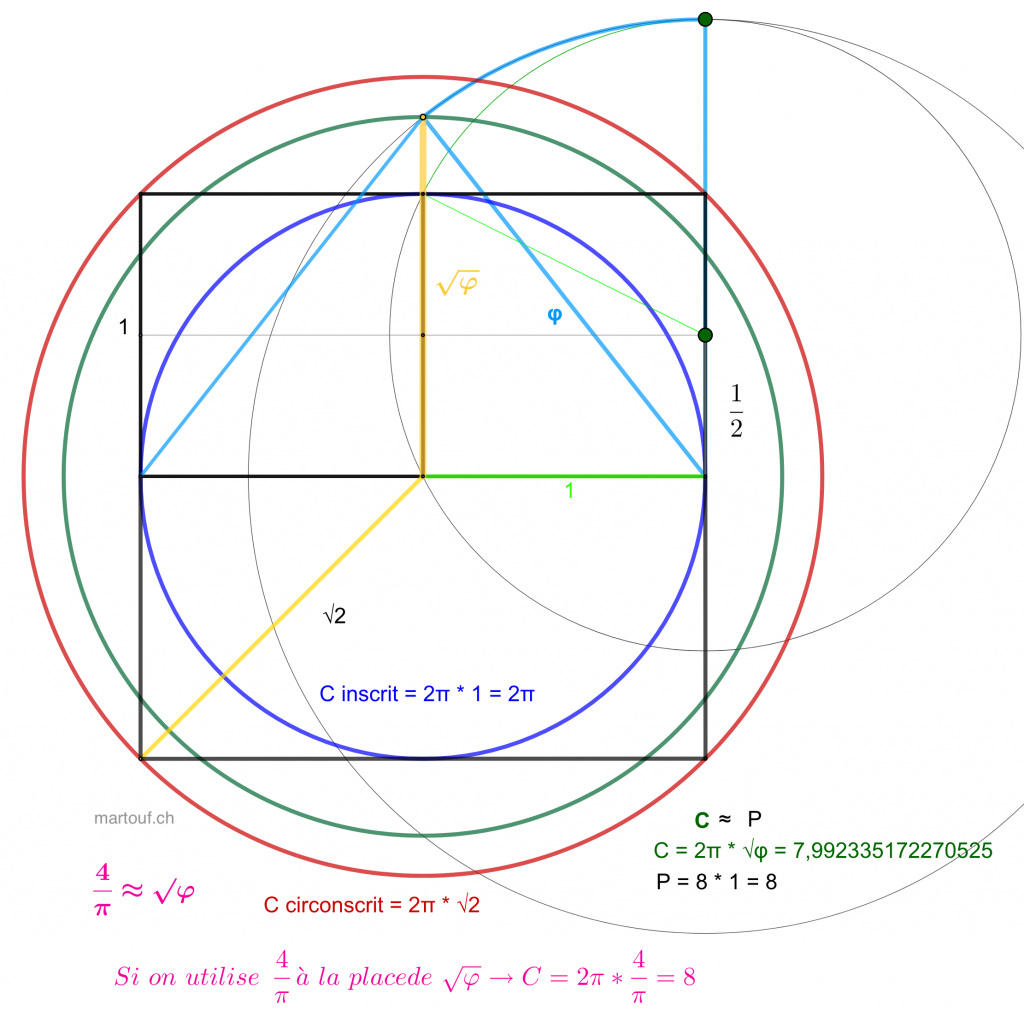
Quadrature du cercle solution geometrie sacree pi racine nombre or

C'est peut être beaucoup d'informations d'un coup. On verra ci-dessous d'où viennent ces traits de construction. Ces formes, ces diagonales et tout ces nombres remarquables que l'on retrouve tout le temps en géométrie sacrée.

A force de les voir on commence à les savoir par cœur et être capable de faire le lien entre une proportion géométrique, son expression mathématique algébrique et sa notation numérique.

Valeurs numériques de nombres courants en géométrie sacrée

Afin de faire le lien entre les anciens et nous, voici les nombres les plus couramment utilisés en géométrie sacrée en expression algébrique et dans leur équivalent en notation numérique:

\[φ ≈ 1.61803398875 \] \[ {1 \over φ} ≈ 0.61803398875 \] \[ {φ^2 } ≈ 2.61803398875 \] \[ √5 ≈ 2.2360679775 \] \[φ = {1 + \sqrt{5} \over 2} ≈ 1.61803398875\] \[{1 \over φ} = {2 \over {1 + \sqrt{5}}} ≈ 0.61803398875\] \[e ≈ 2.71828182846\] \[e ≈ {φ^2 } + {1 \over 10} = 2.71803398875 \] \[√φ ≈ 1.27201964951 \] \[{4 \over π} ≈ 1.27323954474 \] \[ √φ ≈ {4 \over π} \] \[√3 ≈ 1.7320508075688772935\] \[√2 ≈ 1.41421356237\] \[ \cos{π \over 6} = {\sqrt{3} \over 2} ≈ 0.86602540378 \] \[ π ≈ 3.141592653589793 \] \[ {π -φ^2} ≈ 0.52355866484 \] \[ {π \over 6} ≈ 0.5235987756 \] \[ {φ^2 \over 5} ≈ 0.52360679775 \] \[ {5 \over 6 }π ≈ 2.61799387799 \] \[ {φ^2} ≈ 2.61803398875 \] \[ {1+2+ \sqrt{5} \over 10} ≈ 0.52360679775 \]

L'essentiel des nombres à retenir

Le nombre d'or

φ = le nombre d'or = 1.61803398875...
Mais aussi ses déclinaisons, comme son inverse qui = 0.61803398875... (1 de moins) et son carré φ^2 = 2.61803398875... (1 de plus)

Là autour, il y a plein d'approximations très proches faites à base du nombre π. Comme 5/6 π ≈ 2,61799387799...

C'est très étonnant que ces nombres si spéciaux puissent avoir des liens d'approximation si serrés.

Mathématiquement ces liens sont des approximations et pas des valeurs exactes. Il y a une page wikipedia qui les recense comme des coïncidences mathématiques.

Dans une réalisation architecturale, vu que l'on est pas dans le monde idéal des mathématiques, mais dans un monde où les dimensions ont une marge d'erreur, dans un monde où la précision n'est pas infinie. Dans ce cas, que l'on utilise la valeur exacte où une approximation, le bâtiment construit sera le même.

La géométrie sacrée étant principalement utilisée pour créer des bâtiments, certaines personnes n'hésitent pas à faire des raccourcis et dire que des approximations sont des égalités....

....Puis les puristes des maths leur sautent à la gorge.. et on voit des combats. Il y a de trolls qui polluent les espaces de commentaires sur le net en débats stériles de savoir si ce sont des approximations ou des valeurs réelles.

Pour cette raison dans cet article, je tente de bien distinguer les approximations des valeurs réelles mathématiques.

Cathédrale Notre Dame Paris polaroid structure H

La coudée royale égyptienne

Il existe deux définitions mathématiques simple de la coudée royale égyptienne:

0,523606... mètre = φ^2/5 mètre
→ 1/10 du périmètre du triangle des bâtisseurs en mètre (triangle rectangle don l'hypoténuse est la diagonale d'un double carré.)
0,523598... mètre = π/6 mètre
→ 1/6 de la circonférence d'un cercle de 1m de diamètre

triangle des bâtisseurs origine coudée royale égytienne

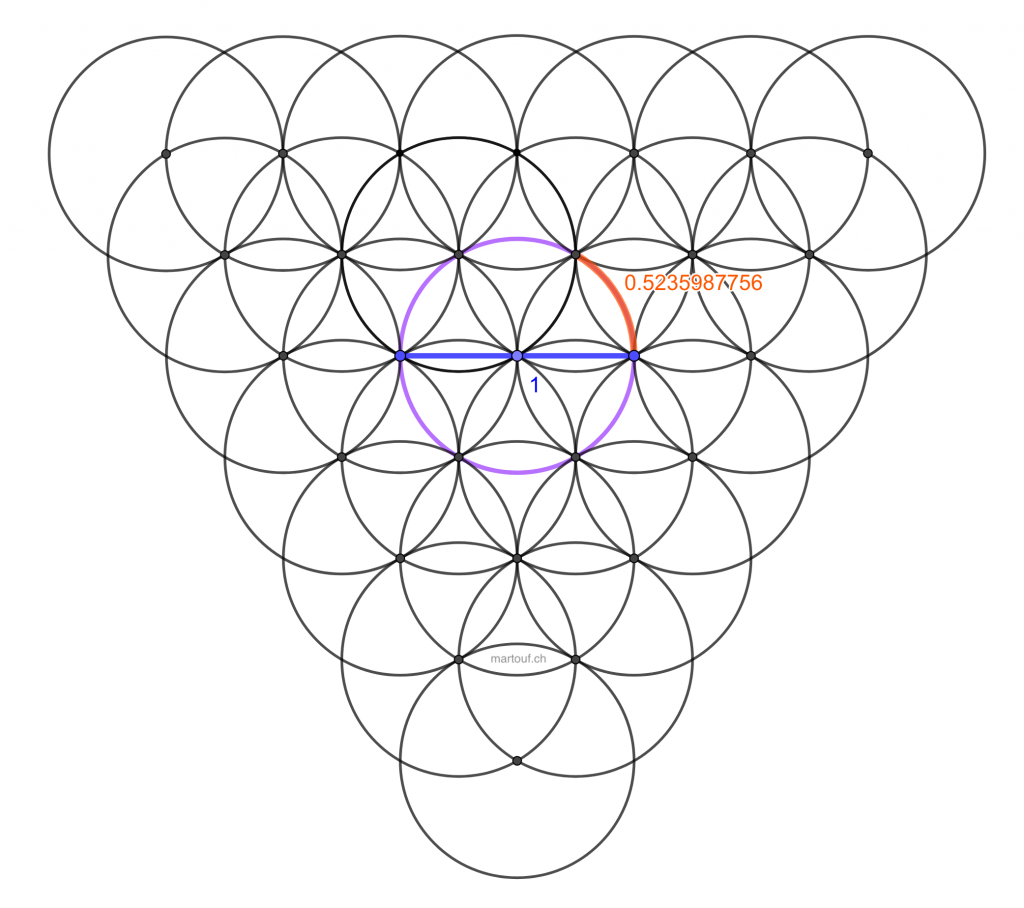
fleur de vie origine coudee royale egyptiennen

Il est à noter que la coudée royale égyptienne est la même que la coudée utilisée par les bâtisseurs de cathédrale dans le système de "quine des bâtisseurs" (aussi appelé parfois "pige des bâtisseurs" et qui sert à construire des outils comme la "canne des bâtisseurs")

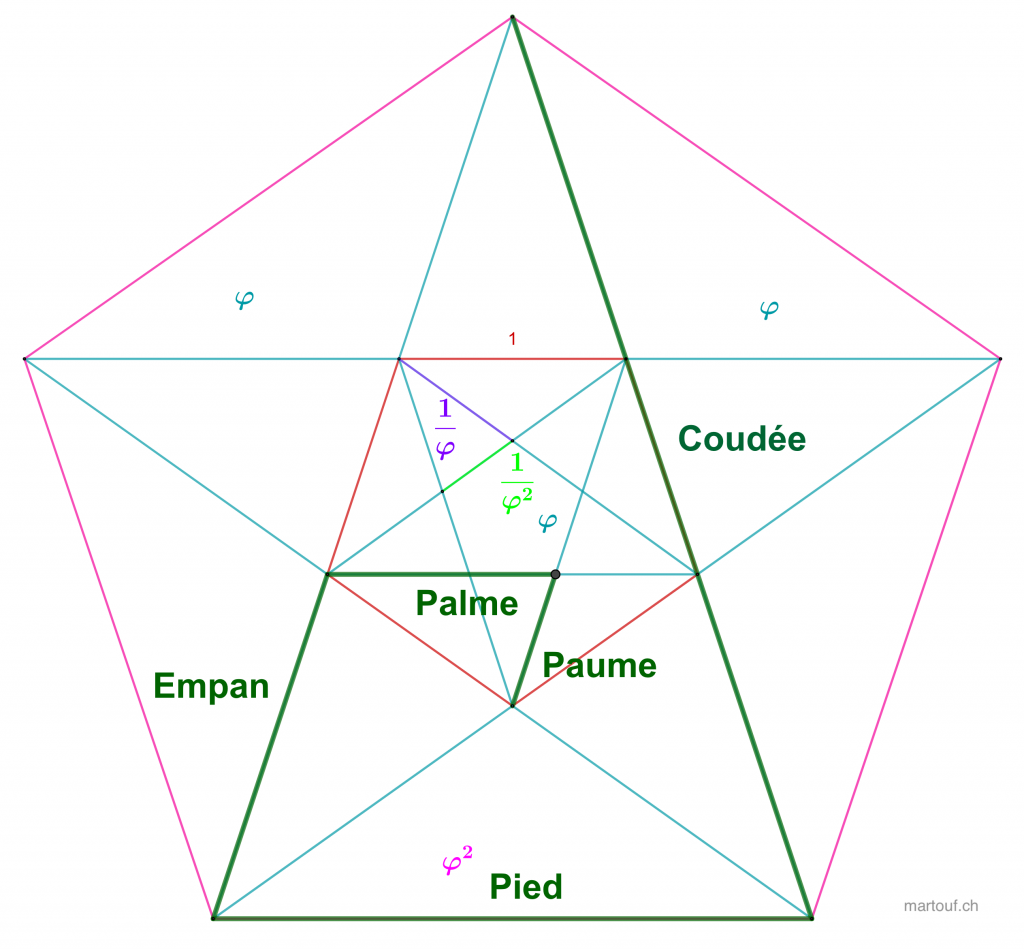
Quine des bâtisseurs de cathédrale un système de mesure imbriqué fractalement avec un rapport du nombre d'or. On le voit bien dans un pentagramme.

Dans ce cas, je viens d'introduire la notion d'unité de mesure. Soit un nombre dans une proportion pure, mais qui est lié à une dimension physique concrète.

Il y a de nombreuses relations mathématiques qui peuvent mener à la définition de la coudée royale. Tout ceci fait encore largement débat. Je n'entrerai pas dans plus de détail dans cet article introductif déjà bien long !

Je n'irai pas non plus ici beaucoup plus loin la notion d'unité de mesure ancienne. C'est un vaste sujet qui méritera un articles complet. (coudée royale, pied, yard mégalithique, pied romain, coudée de Nippur, origine du mètre.. etc..)

Cascade des racines carrées

Maintenant que les bases sont posées. Maintenant que tu as eu l'occasion de comprendre que les anciens avaient un rapport aux mathématiques très différent de ce qui se fait actuellement. On va pouvoir entrer dans le vif du sujet.

Voici la construction de l'essentiel des nombres dont on a besoin et ceci juste à partir d'un carré de 1 de côté. (toujours sans dimension, juste une proportion.)

C'est une cascade de diagonale. On commence par dessiner le carré de 1 de côté. Sa diagonale vaut √2.

Puis on reporte cette diagonale pour créer un rectangle avec un côté qui vaut √2 et l'autre qui vaut toujours 1. La diagonale de ce rectangle vaut √3.

Puis on procède de la même manière, on reporte à nouveau la diagonale de ce rectangle pour obtenir un nouveau rectangle et on obtient une diagonale qui vaut √4 = 2.

Et là, c'est magique. A partir d'un seul carré, on en a maintenant deux !

geometrie-sacrée geogebra-cascade-racine-diagonale-moyen-martouf

Le double carré, le bi-carré est une forme très importante de la géométrie sacrée. C'est depuis cette forme que l'on peut générer toute une géométrie liées à φ , le nombre d'or. Ceci car la diagonale d'un double carré (en rouge) vaut √5.

Et il se trouve que √5 c'est la somme du nombre d'or et de son inverse !

\[ {1 \over φ} + φ = \sqrt{5} \]

J'ai mis un point sur la diagonale rouge pour montrer la différence ente φ et 1/φ.

On va regarder ça en détail.

Le double carré, la base d'une géométrie du nombre d'or

On a vu ci dessus que le nombre d'or vaut:

\[φ = {1 + \sqrt{5} \over 2} = {1 \over 2} +{\sqrt{5} \over 2} ≈ 1.61803398875\]

On va observer à quoi ça correspond en terme de géométrie.

double carré ou bi-carré dans la géométrie sacrée, base de la génération du nombre d'or

$1$ Si l'on commence sur le point en bas à droite du double carré, on peut obtenir un segment vertical qui fait la moitié du côté, soit 1/2.

Depuis là, on ajoute le segment vert clair. Soit la diagonale d'un rectangle 1/2 et 1. Ce qui revient à la moitié de la diagonale du bi-carré. Soit √5/2.

On voit que ceci correspond tout à fait à l'équation qui nous donne la valeur de φ. Voilà. On a généré la longueur du nombre d'or.

C'est grâce à cette longueur que j'ai pu placer le point rouge qui coupe la diagonale √5 avec 1/φ d'un côté et φ de l'autre.

Ensuite, au centre il y a une droite verticale orangée. Je l'ai générée en faisant croiser la longueur de φ depuis le coin en bas à droite, avec le prolongement du côté commun aux deux carrés du bi-carré.

Voilà, on a ainsi généré un segment de longueur √φ.
(Petit rappel, chaque nombre est une proportion par rapport au côté du carré qui vaut 1. Donc ici √φ * 1 = √φ . Mais quand on donnera une dimension réelle au côté 1 il ne faudra pas oublier de faire la multiplication par la taille du côté.)

J'ai ici créé un nouveau triangle tout à faire remarquable auquel on peut appliquer le théorème de Pythagore.

\[{{\sqrt{φ}}^2+1^2}= φ^2\]

Il s'agit du triangle de Kepler. Il y a un rapport du nombre d'or entre chaque côté.

Le bi-carré la base de monuments mégalithiques depuis des millénaires

Ce double-carré est vraiment une forme très courante en géométrie sacrée.

Le profil de la grande pyramide de Gizeh (Kheops)

C'est ainsi que la construction du triangle de Kepler obtenue avec le double carré se trouve être le profil de la grande pyramide de Gizeh.

Le côté de la pyramide vaut 2. Ainsi le demi côté vaut 1. La hauteur de la pyramide vaut √φ. Et l'apothème, vaut φ.

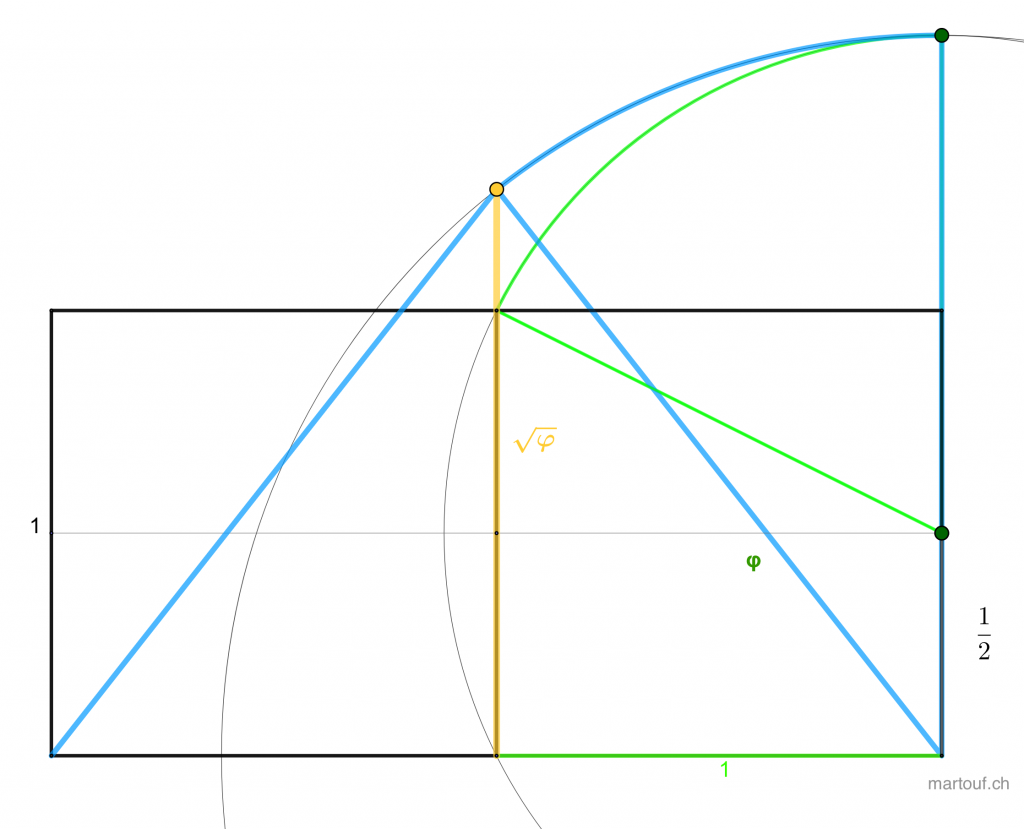
Géométrie sacrée profil de la grande pyramide de Gizeh (pyramide de Chéops) Nombre d'or, triangle de kepler

Le sol de la chambre haute de la grande pyramide de Gizeh est un bi-carré

Pour aller encore plus loin et montrer que ce n'est pas une proportion faite au hasard. La chambre haute de la grande pyramide de Gizeh est aussi construite selon un double carré !

Le sol de la chambre est un bi-carré. Ici on a un monument construit en vrai. Donc il y une dimension. L'unité de mesure utilisée est la coudée royale égyptienne. Pour faire court. Elle vaut ≈ 0,5236 mètre.

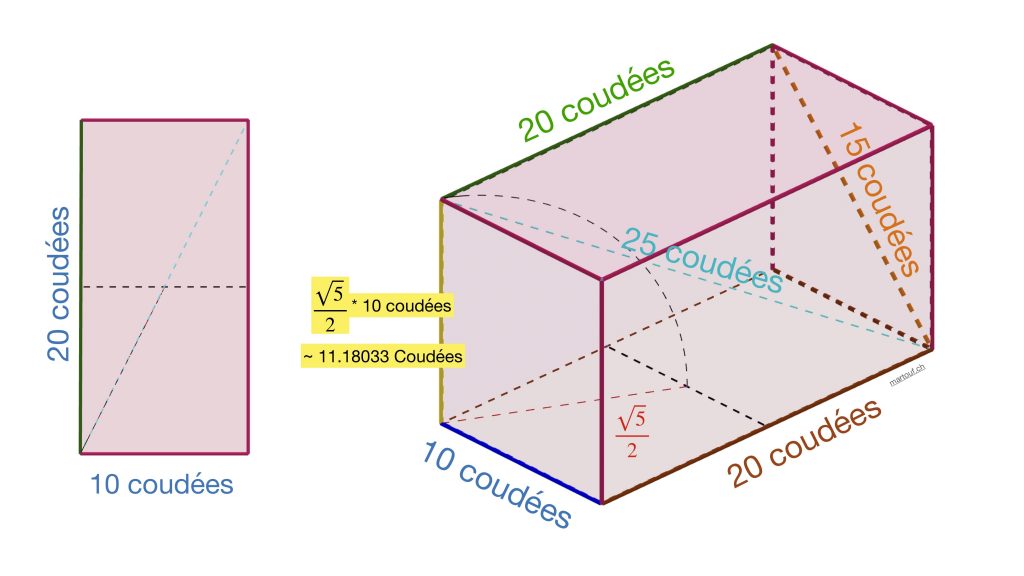
geometrie sacree chambre haute grande pyramide gizeh cheops coudee double carre nombre or

Le double carré de la chambre haute de la grande pyramide est composé de carrés de 10 coudées royales de côté.

La hauteur de la chambre est générée de manière un peu plus subtile. En fait, c'est une demi diagonale du double carré qui est relevé. (Le segment vert sur l'image précédente) On a donc 11,18033 coudées.. ce qui correspond à √5 * φ^2 mètre.

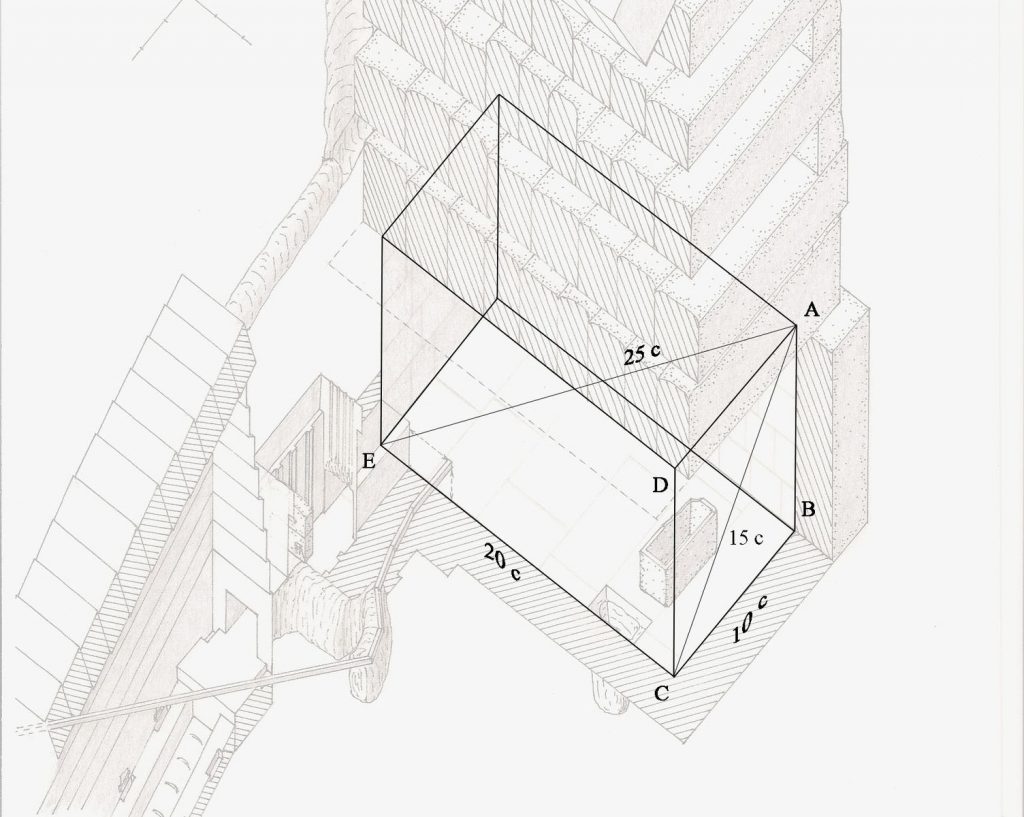
schéma de la chambre haute de la grande pyramide de gizeh. Dite chambre du roi.

Menhirs de Clendy à Yverdon

A des milliers de kilomètres de l'Egypte, mais également à 2 millénaires d'intervalle dans le temps, on retrouve aussi un alignement de menhirs à côté de chez moi qui est construit sur la base d'un bi-carré.

Il s'agit de l'alignement des menhirs de Clendy à Yverdon qui date du IV millénaire avant J.-C.

On ne sait pas si toutes les pierres sont encore là. On sait que le site a été sous l'eau pendant 2000 ans. La plupart des fosses des menhirs ont été découvertes en 1975 et ainsi en 1986 on a pu redresser les menhirs à leur emplacement originel supposé.

schéma directeur en double carré de la construction des menhirs de clendy

Le schéma directeur de construction de ce site est très probablement un double carré. Comme on l'a vu ci-dessus, ce double carré est une porte ouverte à tout l'univers du nombre d'or: pHi.

Cette idée du schéma directeur des menhirs de Clendy vient du livre "Géométrie sacrée" de Stéphane Cardinaux.

J'ai aussi remarqué que l'azimut de l'axe central est à 222°. C'est déjà un joli nombre. Mais c'est pas tout !!

222°, c'est le complément de 137.51° soit l'angle d'or. C'est la variante angulaire du nombre d'or.

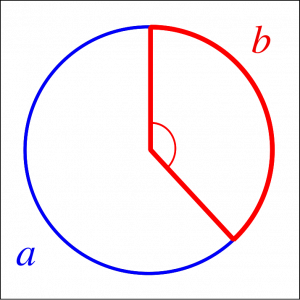
Donc les bâtisseurs de l'alignement de menhirs de Clendy ont réalisé un double carré, une géométrie qui ouvre directement sur le nombre d'or. Mais aussi ont aligné ce double carré avec un angle d'or par rapport au nord. Ceci il y a 6000 ans !

Le triangle 3-4-5

Le triangle 3-4-5 est le premier des triangles rectangles. Il s’agit du triangle rectangle à côtés entiers avec l’hypoténuse minimale, et le seul triangle dont les longueurs de côtés suivent une progression arithmétique.

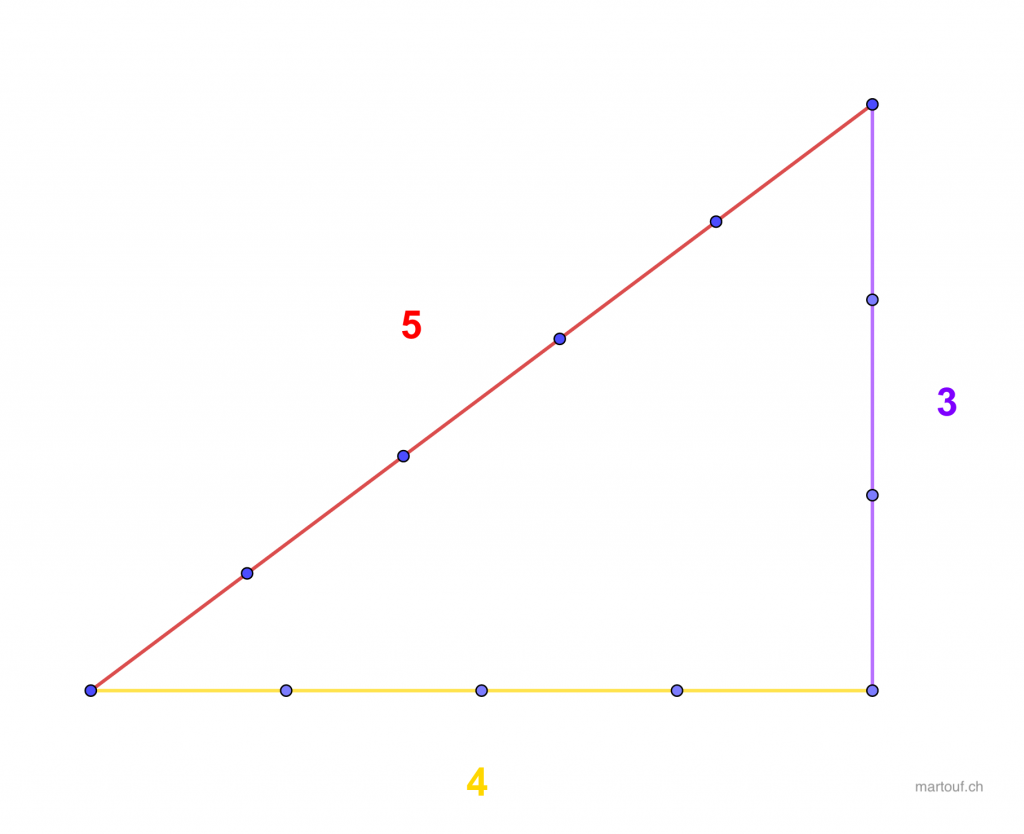
Ce triangle 3-4-5 a des propriétés mathématiques intéressantes qui ont permis de construire un outil très utilisé des arpenteurs et bâtisseurs: la corde à 13 nœuds.

Pourquoi utiliser les nombres 12 et 60 pour diviser le temps ?

Pourquoi est-ce qu'il y a 12 heures sur un cadran de montre ? ⏰
Pourquoi est-ce que l'on divise un heure en 60 minutes, et une minute en 60 secondes ? ⏱

L'explication se trouve dans le triangle 3-4-5.

Avec les chiffres des côtés (3-4-5) on a peut faire une suite arithmétique (addition) et une suite géométrique (multiplication).
(Dans le même genre, le mythique nombre φ est la seule proportion qui est en même temps une suite arithmétique et une suite géométrique. Donc c'est le même genre de logique qu'on cherche avec le triangle 3-4-5)

3 + 4 + 5 = 12
3 * 4 * 5 = 60

J'ai repris cette idée chez Edmée Jomard (un des tout premier égyptologue ayant participé à la campagne napoléonienne en égypte), à la page 225 de son livre: "Mémoire sur le système métrique des anciens Égyptiens, contenant des recherches sur leurs connoissances géométriques et sur les mesures des autres peuples de l'antiquité " publiée en 1817.

Le détail est à la p225.

Jomard tire lui même cette idée du philosophe romain du 1er siècle Plutarque, qui lui-même dit le savoir du philosophe grec Platon (de 400 ans plus vieux). Il est connu que Platon a fait un séjour en égypte chez des prêtres à Héliopolis.

12 et 60 sont de plus des nombres dit "fiables"(selon la définition mathématiques des nombres qui peuvent se diviser facilement, donc très pratique pour faire des divisions horaires.)

Si on continue les propriétés mathématiques de ces nombres:
12*60 = 720
12+60 = 72

Magique non ?

Conclusions: tu as les bases pour explorer le monde

Maintenant que nous arrivons au terme de cette introduction (déjà hyper complète) à la géométrie sacrée, tu as les bases pour voir les monuments sous un regard neuf. Tu as de quoi décrypter les intentions des bâtisseurs.

Géométrie plutôt que chiffres à virgule

Si l'on se remémore les points importants, il faut se souvenir, que les anciens bâtisseurs n'ont pas le même rapport aux mathématiques que nous. Ils privilégient la géométrie, le dessin et pas les nombres en notation à virgule.

Des proportions en résonance fractale

Les anciens bâtisseurs aiment construire des bâtiments où les proportions de chaque élément sont en résonance les un avec les autres par des proportions.

La proportion la plus connue, et la plus "magique" étant la proportion dorée. Cette proportion qui met en lien le tout et sa partie de manière fractale.

Les anciens ont utilisé les propriétés de cette proportion dorée comme support d'un système d'unité de mesure avec la quine des bâtisseurs.

En prenant conscience que ces unités de mesure antiques ne sont pas juste des mesures étalonnées sur les pieds ou bras des monarques, mais sur des relations mathématiques, c'est toute une compréhension du monde qui s'ouvre.

Ceci, bien qu'en fait, le corps humain est, comme beaucoup de choses dans la nature, structuré sur la base de proportions de géométrie sacrée, et notamment autour du nombre d'or. Il n'est donc pas faux de dire qu'il y a un lien entre la mesure de partie du corps humain et des unités de mesures. Mais ce n'est pas QUE ça. Il ne faut pas oublier le sous-jacent mathématique.

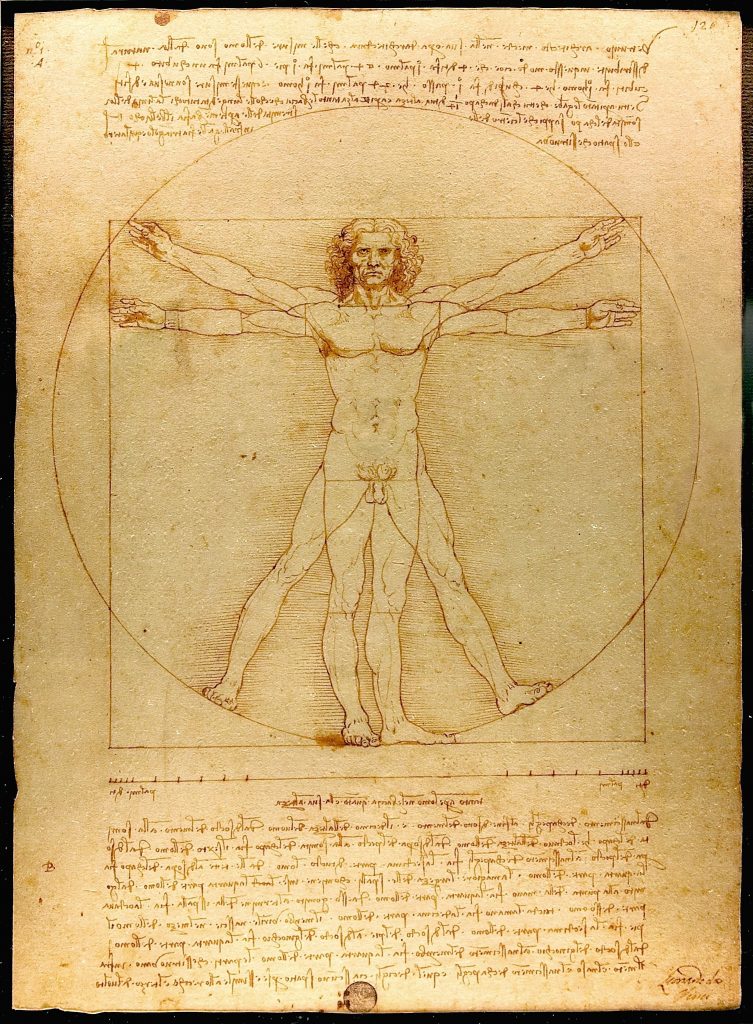
La géométrie sacrée relie tout. Elle fait entrer en résonance les humains et les constructions qu'ils habitent.

Ainsi, un temple, une cathédrale, une pyramide, un alignement de menhirs est généralement construit avec de la géométrie sacrée.

Les mêmes principes de construction se retrouvent du microcosme au macrocosme, de l'humain aux galaxies.

« Ce qui est en bas est comme ce qui est en haut, et ce qui est en haut est comme ce qui est en bas »

Cette citation est un des principaux enseignement d'Hermès Trismégiste que l'on retrouve dans la Table d'émeraude.

Exemple pratique de décodage de la géométrie sacrée d'une cathédrale

Quand on est quelque peu "initié" à ces connaissances hermétiques (comme la fermeture des boites Tupperware... :p ) il est possible de voir dans un tas de caillou un sens plus profond.

Voici un exemple pour illustrer mes propos.

Avec l'œil ouvert, il possible de repérer des pierres spéciales dans un simple dallage de cathédrale. Voici la pierre angulaire de la cathédrale de Fribourg.

pierre angulaire de la cathédrale de Fribourg — Pierre angulaire de la cathédrale de Fribourg

Ce sont en fait deux pierres allongées en granite. Le granite est très solide et ne se dilate pas. Cette pierre a du servir comme étalon de mesure pour construire la cathédrale. En fin de chantier elle a été intégrée au dallage.

Mesure de la diagonale de la pierre angulaire de la cathédrale de Fribourg

Comme on l'a vu ci-dessus, en géométrie sacrée c'est souvent la dimension des diagonales qui compte, et là on ne va pas être déçu....

Mais au passage, sache déjà que le petit côté de ce rectangle est formé par deux fois 1 pied romain. (29,635 cm)
(Le pied romain est toujours très utilisé de nos jours... c'est la hauteur d'une page A4 !!! soit 29,7cm)

pierre angulaire de la cathédrale de Fribourg detail mesure diagonale 1 metre

La diagonale de la pierre angulaire de la cathédrale de Fribourg vaut 1 mètre !!!
... et oui, le mètre est bien plus ancien qu'on le dit officiellement.
Il y a de nombreuses portes de monuments du XI au XVIII ème siècle qui ont une taille liée au mètre.

Il se pourrait même que le mètre soit déjà présent sur des constructions mégalithiques beaucoup plus anciennes...

De plus comme évoqué plus haut, il y a un lien entre le mètre et la coudée royale égyptienne.

Il est peut être à rappeler que le mètre est directement lié à la mesure de la circonférence de la Terre. Cette mesure a déjà été réalisée avec précision dans des temps assez anciens.

Ainsi en géométrie sacrée, le mètre est une unité de mesure qui permet de mettre en lien, en résonance avec la dimension de la Terre.

🌍

Au tout début de cet article, j'ai insisté sur les proportions. Sur des liens entre grandeur sans dimensions.

Je termine cet article en reliant ces proportions à une dimension, à une échelle. Ceci se fait avec des unités de mesure.

Ainsi la présence du mètre dans la pierre angulaire de la cathédrale de Fribourg me fait penser que celle-ci a des proportions qui sont reliées à la dimension de la Terre.

Voilà, je te laisse maintenant voir le monde et les monuments anciens avec un œil neuf.

le Grand architecte de l universe God_the_Geometer — Dieu l'architecte de l'univers, frontispice d'une bible moralisée.

Merci au logiciel geoGebra qui m'a permis de réaliser les nombreux dessins de géométrie sacrée.

Mes notes à propos du documentaire BAM – Les Bâtisseurs de l’Ancien Monde

Mes notes sont encore très but…. Mais c’est déjà ça… « release early, release often… »…

Le documentaire BAM les Bâtisseurs de l'Ancien Monde est sorti en novembre 2018.

Voici la bande annonce:

C'est le nouveau film de Patrice Pouillard, le réalisateur du très connu et controversé documentaire: la révélation des pyramides.
Mes notes à propos de la révélation des pyramides sont ici... et ci-dessous, je vais donc faire une telle page à propos de BAM - Les Bâtisseurs de l'ancien monde. Car il y a de nombreux sujets qui m'interrogent et que j'ai envie de développer.

Voici le film complet:

Genèse du film Bâtisseurs de l'Ancien Monde

L'origine de BAM est pleine de rebondissements. A l'origine c'était la suite de la Révélation des pyramides. Mais suite à une brouille entre le réalisateur et l'informateur. Le film BAM est en fait devenu une sorte de Reboot...

Certaines mauvaises langues disent que ce film est nul et n'apporte rien de plus, car la vraie source, l'informateur n'est plus aux commandes...

Il est vrai qu'il y a de nombreux thèmes qui sont semblables et repris. (notamment la notion de lien entre la coudée royale égyptienne et le mètre, les constructions cyclopéennes de part le monde qui sont énormes, vieilles et anti-syssmiques, la notion de grand cercle...)

Cependant, il y a aussi pleins de nouveaux sujets étonnants et bien fouillés, je pense notamment aux grottes de Barabar et à la machine d'Anticythère.

On peut dire que ce film Bâtisseurs de l'ancien monde est un reboot de la révélation des pyramides, ou un remake... mais, le réalisateur a pris le temps de voir les critiques faites à son film précédent, de reformuler correctement certains propos et d'expurger ce qui n'est pas fiable. (notamment son informateur qui a tendance à prétendre tout et son contraire et ne veut jamais montrer ses sources ! .. mais qui malgré tout apporte des idées à creuser...)

Je trouve que ce film apporte des faits tout à fait intéressants qui font réfléchir à la question posée....

Sommes nous la premières civilisation "avancée" sur cette planète ?

J'espère que ce film sera largement vu et que l'on creusera encore plus les sujets qui sont soulevés. C'est la raison pour laquelle je fais cet article.

https://vimeo.com/ondemand/batisseursdelancienmonde

Pour voir le film BAM - Bâtisseur de l'Ancien Monde en streaming, c'est tout simple... c'est par ici.... pour la modique somme de π € 😉

Le fameux bloc H en pierre

Sur le site de Puma Punku en Bolivie, il y a des blocs en pierre en forme de H. Il se trouve que ces blocs sont nombreux... et si on mesure leur hauteur ça fait.... exactement.... 1 mètre !

Fabrication industrielle ?? Surtout qu'il y a plusieurs exemplaires !

On retrouve ce H aussi sur les piliers de Gobekli Tepe en Turquie.

Voici un extrait du film qui présente les H de Puma Punku..

Pas dans le film, mais permet d'en savoir plus sur le sujet.

En octobre 2018, Joseph Davidovits et l'institut géopolymère ont sorti une étude des roches rouge sédimentaire de Tihuanaco et des blocs d'andésite de Puma Punku (les H ).
Il semble bien que ces roches sont des géopolymères. Donc les roches n'ont pas été taillées, mais moulées !

Les pierres rouges sont probablement faites avec un géopolymère avec catalyseur alcali.
Les blocs en H sont probablement faits avec un géopolymère avec catalyseur acide.

L'acide proviendrait de diverses plantes qu'on trouve dans les environs... ce qui correspond à la légende locale qui dit qu'il existe une plante pour ramollir la pierre ! .. bref un acide ! Un article scientifique sur le lien entre les plantes et la fabrication de pierre est en cours de relecture par les pairs...

Voici un lien vers l'article scientifique "Ancient geopolymer in south-American monument. SEM and petrographic evidence" dans la revue Elsevier...

Davidovits a déjà montré que certaines pierres des pyramides de Gizeh sont des géopolymères à base de calcaire. On le voit grâce à l'étude paléomagnétique des pierres des pyramides de Gizeh. Les moments magnétiques de la pierre sont alignés et prouvent que ce n'est pas la sédimentation qui a fait la pierre.

Voici une vidéo qui explique la technique utilisée en Egypte pour fabriquer des pierres en calcaire ré-aggloméré (géopolymères) et les mouler pour faire des blocs de construction des pyramides.

Avec l'andésite, c'est nouveau. C'est une roche volcanique. L'étude montre qu'il y a des matières organique dans les blocs, ce qui n'est absolument pas naturel !!

Voici l'extrait au bon endroit (39 mintues, soit 7 minute avant la fin) de l'annonce de Joseph Davidovits à propos de l'étude faite à Puma Punku qui montre que l'on a des géopolymères.

Les géopolymères sont à mon avis une très très bonne explication de beaucoup de mégalithe dont on se demande comment ils ont été déplacé tellement les blocs sont énormes, ou comment ils ont été taillé tellement la roche est dure (comme l'andésite). Ça explique aussi la fabrication de nombreux artefact que l'on trouve dans les musées comme le disque de sabbu et autre "plats" qui sont en schiste tout fin et replié.. choses quasi impossible à faire à la taille sans casser la roche.

De plus les géopolymères explique certainement la fabrication de nombreux vases en roche très dure (comme le gneiss) que l'on a retrouvé sous la "pyramide" à degré de Djoser à Saqqarah. (ou encore ce mini "bol tout replié")

Pour en savoir plus sur la pierre moulée de type géopolymère, j'ai écrit tout un article sur le sujet... c'est par ici....

L'avis du tailleur de pierre et bâtisseur de cathédrale Jean-Louis Boistel

Dans le film, on voit Jean-Louis Boistel s'exprimer. C'est un tailleur de pierre, à l'ancienne. Il a fait des études de "bâtisseur de cathédrale".. si si, ça existe encore ! Il dit que ça prend 10 ans !

Dans les bonus de BAM, il y a quasi 1h30 d'interview de Jean-Louis Boistel.

Voici la bande annonce de ce bonus....

Le film et les autres bonus sont par ici...

Dans cet interview on lui pose des questions sur les techniques de construction de divers murs un peut partout dans le monde. C'est souvent sur la base de photos qu'on lui apporte.

Voici un bref résumé de ce qu'il dit.

Selon lui, on peut tailler du granite sans trop de soucis. Mais pas avec du matos de castorama... avec des bons outils qui proviennent d'un excellent forgeron. (il dit même qu'il a connu un forgerons magicien qui lui a fait des outils qui n'ont pas eu besoin d'être reforgé en 30 ans d'utilisation !)

Il privilégie donc les outils forgés à la main. En fer... et pas au tungstène.... !!
Très intéressant qu'il dise que c'est possible. Car souvent on nous le présente comme "impossible".

Par contre il trouve que c'est impossible de faire ce que l'on voit en égypte sur du granite avec des cailloux comme outils ! (la réponse standard des égyptologues quand à la taille des obélisques.)

Jean-Louis Boistel pense que les sculptures en granite Egyptiennes sont certainement faites avec des outils en fer forgé. Il en discute avec des amis égyptologues tailleurs de pierre qui semblent d'accord avec lui.

C'est contraire à l'avis majoritaire des égyptologues qui prétendent que les outils en fer n'existaient pas. Mais quand on voit les découvertes très récentes sur les pigments du bleu égyptien qui est fluorescent et qui permet de refroidir les batiments..... moi je me dis qu'on est encore loins de tout savoir sur la techniques de pointes d'il y a quelques millénaires ! Tout est possible !

Si il y avait des outils en fer, alors pourquoi est-ce que l'on ne retrouve pas ces burins ?
=> il évoque le fait que les métaux sont rares et systématiquement reforgés, ou transformés en clou... donc plus c'est ancien.. moins on retrouvera de trace d'outil.

Jean-Louis Boistel évoque aussi quelques techniques de bâtisseurs de cathédrales pour déplacer des gros blocs. Il dit que ces techniques sont en voie de disparition tellement on abuse de l'utilisation des machines. Il suppose que peut être dans le passé il y avait encore d'autres techniques qui ont disparues ?

A propos d'un des coffres du Serapeum de Saqqarah: Il faut beaucoup beaucoup beaucoup de temps, les bons outils sont nécessaire, mais ça ne suffit pas. "En voyant ça on pense machine...".

Quand on lui montre une photo d'un bloc de pierre de Tiahuanaco, (à 1h15) il dit:

"Ce qui est quand même un peu curieux, c'est qu'on voit un négatif d'autres éléments qui viennent s'emboiter dedans ou qui sont derrière..... Un peu comme si tout ça s'était de l'agglomérat coulé sur une structure porteuse en autre pierre..... Voyez les joints, les espèces de traces que l'on a, qui correspondent peut être à chaque carré. Un peu comme ce que l'on obtient quand on fait des découpes machine sur des blocs de pierre.... aujourd'hui."

Quand j'entend un tailleur de pierre autant qualifié dire que ça ressemble beaucoup à un agglomérat de pierre moulée.... et que d'un autre côté, le prof. Davidovits publie un article scientifique qui dit que les pierres de Tiahuanaco sont des géopolymères, donc de la pierre moulée....

... et bien je crois que là on a résolu le mystère. Non ?

Interview passionnant d'un passionné !

La machine d'Anticythère

Voici un extrait du film à propos de la machine d'Anticythère. C'est hallucinant de savoir qu'il y a 2000 ans il existait des appareils aussi sophistiqués !

Ciceron avait même parlé de l'existence d'une telle machine, mais de la trouver c'est encore autre chose !

Le coup des engrenages qui "respirent" pour adapter la vitesse des engrenages est vraiment un des points les plus passionnants de ce film !

Voici quelques aperçus de ce à quoi devait ressembler cette machine d'anticythère:

Petite question proposée dans le film:
"Comment diviser un cercle en 223 parties ?"
=> Si t'as une idée... indique là dans les commentaires.

Les grottes de Barabar en Inde

Les grottes de Barabar sont des grottes creusées dans des rochers dans le nord de l'Inde.

Gopika
Vadathika
Vapiyaka
Karan chopar
Visva zopri
Sudama
Lomas Rishi

Les grottes de Barabar sont tout à fait remarquables pour leur géométrie et surtout leur finition. Les surfaces sont plus lisses que du verre !!!

Les surfaces ont été mesurées à l'aide d'un rugosimètre. Il y a des surfaces lisses avec des aspérités de l'ordre du micron !

Une des questions soulevées par le film, c'est.... comment les bâtisseurs s'éclairaient ??

C'est pas dans le film, mais voici une piste de réponse.... à l'électricité !
Voici comment créer une batterie à partir d'un texte du sage Indien Agastya qui a vécu il y a 4000 ans !!

Cuivre + zinc + sciure de bois + sulfate de cuivre (cou de paon en langage alchimique)

Sur l'entrée de certaines de ces grottes il y a des inscriptions commanditées par l'empereur Ashoka vers - 260. Elles indiquent que l'empereur offre ces grottes à une secte d'ascète de l'époque.

Ce qui surprend, c'est la grande différence de précision entre les inscriptions et la surface de la grotte. Ça semble montrer que ce ne sont pas du tout les mêmes outils et commanditaires.

La géométrie des grottes de Barabar est également tout à fait intéressante. Il y a des effets de résonance du son. Les grottes sont même souvent appelées "Grottes sonores".

Un scan 3D des grottes a été réalisé pour mieux observer leur géométrie.

On voit qu'il y a une grotte qui est restée inachevée.... et/ou que l'on a tenté de terminer et qui a été loupée...

La surface des grottes de Barabar n'est pas sans rappeler un autre site. Le Serapeum de Saqqarah et ses coffres à boeufs tout lisse.

Il est même étonnant que là aussi, il y a un coffre inachevé.... ça semble être la règle chez les bâtisseurs de l'ancien monde. Tout comme il y a des Moaï inachevés sur l'iles de Pâques (on les voit au début du film et où il sont placés.. ça remet en cause la théorie qui dit qu'ils sont justes glissés pour les lever.), il y a l'obélisque inachevé d'Assouan, et on vient de le voir ci-dessus il y a un grotte inachevée à Barabar...

La précision du polissage des coffres à boeufs n'est cependant pas autant bonne que celle des grottes de Barabar... mais bon à moins de 3 microns... c'est pas mal non plus !

Mesure des grottes sonores de Barabar

Pour le film les bâtisseurs de l'ancien monde, des mesures des résonances sonores ont été effectuées dans les grottes de Barabar.

On découvre que malgré les formes diverses et variées des grottes. Elle résonnent toutes à 200Hz. On dirait bien que c'était là la fonction de ces grottes. Mais pourquoi ?

La grotte de Sudama a des mesures tout à fait étonnante. On a un rayon de sphère qui est de 6 mètres, dont le centre est posé à 1 mètre de hauteur !

Encore une fois, le mètre semble être connu depuis des millénaires !

Quine des bâtisseurs

Déjà dans La révélation des Pyramides on abordait le fait que la coudée royales égyptienne est basée sur le 6ème d'un arc de cercle dont le diamètre vaut 1 mètre ! (pi/6 en mètre)

Dans BAM, on en rajoute une couche pour parler du système d'unité de mesures des bâtisseurs de cathédrales. Soit, la quine.

Il s'agit d'un système de mesure qui est basée sur des rapports du nombre d'or.

On a là des proportions de longueur. Mais il faut encore calibrer ces longueurs sur une dimension précise. Il se trouve que l'empan vaut 20cm soit... 1/5 de mètre !

Il semble bien que le mètre, qui n'est qu'une fraction de la circonférence de la Terre, soit connu depuis longtemps.

Dans le film BAM, on voit Quentin Leplat qui nous parle d'une étude statistique qu'il a faite sur les portes d'église et il nous indique que l'on trouve fréquemment des portes qui font 1m de largeur ! (où des mesures dérivées)

Gobekli Tepe

Ce lieu chamboule complètement les idées sur l'évolution de l'agriculture et de la sédentarisation.

A Gebekli Tepe, il y a des enceintes avec des mégalithes gravés. Les traits sont très fins. Le site a été découvert dans les années 1990... (bien qu'on savait depuis 1963 qu'il y avait des anciennes traces d'habitations humaines)

Le site a été très bien conservé, car il a été intentionnellement enfoui !! Pourquoi ?

Il y a encore de nombreux cercles qui sont sous terre. Il y aurait donc 16 cercles. Ce qui représente près de 250 mégalithes.

La datations des éléments les plus anciens remontent à près de 14 000 ans ! A cette époque, il n'y avait pas d'agriculture !

Ceci chamboule la théorie qui dit que pour construire, pour avoir une organisation capable de construire un tel site, il faut avoir déjà passé la révolution agricole, ce qui laisse du temps pour faire autre chose que se nourrir.

A Gobekli Tepe... il y a des sculptures de panier.

Ceci rappelle l'histoire du dieu civilisateur mésopotamien Oannès. Un dieu souvent représenté avec un panier. Un dieu qui est venu enseigner l'agriculture aux peuples.... et ça ne semble pas le seul dieu civilisateur avec un panier....

Petite subtilité.... Gobekli Tepe signifie La colline du Nombril....
Il doit y avoir pas mal de nombrils sur cette planète, déjà Rapa nui, l'ile de pâques est le nombril du monde... mais aussi Cuzco...
(On voit tout ces lieux dans le film...)

Une ancienne civilisation victime d'un cataclysme ?

On peut se demander si tout ces nombrils ne seraient pas des lieux d'enseignement des dieux pour apprendre au peuple la civilisation.

Les dieux seraient des rescapés d'une ancienne civilisation victime d'un cataclysme. Il y a un légende persistante dans tous les peuples. C'est le mythe du déluge.

Ce déluge ne tombe pas de nulle part.

Il y a une période appelée le Dryas récent pendant laquelle il y a eu des changements climatiques importants. La température a chutée de 7°C puis est remontée de 10°C, ce qui a entrainé une montée des océans de l'ordre de 120m. On peut aisément imaginer que des régions peuplées aient été victime d'un engloutissement.

On retrouve d'ailleurs des vestiges engloutis. Notamment dans l'océan Indien. Le tsunami de 2004 a eu pour effet de découvrir pendant 30 minutes des vestiges proches des côtes.

Est-ce que ce serait là le début du mythique continent de Kumari Kandam dont parle la tradition Tamoule ? Ce continent est souvent associée à la Lémurie.

Graham Hancock a écrit le livre Magiciens des Dieux qui va tout à fait dans ce sens. Il est interviewé dans BAM - Bâtisseurs de l'Ancien Monde et indique que sur les murs du temple d'Edfou en Egypte il y a toute une histoire qui raconte l'arrivée des Dieux en Egypte suite à la destruction de leur pays d'origine.

J'aimerai bien avoir la traduction de ce texte ! J'en ai trouvé quelques fragments sur le site d'Anton Parks qui lui aussi reprend cette idée pour son livre La dernière marche des dieux.

Une université allemande est en train de finaliser la traduction intégrale des hiéroglyphes du temple d'Edfu. Mais le travail ne semble pas encore totalement publié...

Graham Hancock en Bonus dans BAM

Le film BAM contient aussi 11h de bonus !!

Là il y a beaucoup de matière pour aller plus loin.

Voici notamment le bonus avec 1h15 d'interview de Graham Hancock qui aborde de nombreux sujets.

Dans ce bonus il répond notamment à une des question que je me posais... Où est-ce que l'on peut avoir une traduction du texte qui est sur les murs du temple d'Edfu.
Il recommande de s'intéresser aux travaux de l'égyptologue Eve A. E. Reymond.

Je vois qu'elle a écrit tout un livre: The Mythical Origine of the Egyptian Temple. Quelques extraits sont visibles sur google books.. sur amazon le livre est vendu plus de 300 $ !! ... Il doit pas être très courant !!

... Quelques infos sont disponibles ici dans ce livre: The Cygnus Key: The Denisovan Legacy, Gëbekli Tepe, and the Birth of Egypt de Andrew Collins.

Ouais.. en effet, comme le doit Graham Hancock, c'est pas simple à trouver les infos !

Il parle encore d'un truc que j'avais jamais entendu, c'est l'idée que la précession des équinoxe qui nous fait changer de "paysage" céleste, ne serait pas forcément le fruit d'une variation de la Terre qui bouge sur son axe de rotation, mais plutôt d'une orbite de tout le système solaire autour de l'étoile Sirius, un système binaire.

Cette thèse est développée par Walter Cruttenden et le Binary Research Institute.

Il y a encore beaucoup d'autres choses dans cette interview... J'en parlerai plus tard quand je prendrai le temps de le faire.. en attendant.. regarde cette vidéo:

BAM ITW - GRAHAM HANCOCK *** VO SOUS-TITRÉE *** from BAM INVESTIGATIONS on Vimeo.

=> le streaming a changé de plateforme.. donc ce bonus de BAM se retouve par ici...

Une connaissance ancienne de la géométrie de la Terre

Les nombreuses références au mètre, ainsi que la machine d'Anticythère semblent nous indiquer que depuis très longtemps, il y a des gens qui ont une connaissance précise de la géométrie de la Terre. (Géo .. la terre.. mètre... mesure !)

En moins sophistiqué que la machine d'Anticythère, mais en pas mal plus vieux aussi, perso, j'aime bien le disque de Nebra. Le réalisateur a été voir cet objet, mais je ne sais pas pour quelle raison, il a été écarté du film. Il est à remarquer que ce disque peut aussi être considéré comme un "ordinateur" astronomique et que la circonférence du disque fait.. 1 mètre !

Il semble plausible qu'une civilisation ayant ces connaissances ait existé il y a quelques millénaires et qu'elle a été détruite, ne laissant que quelques rescapés qui ont été enseigner leur savoir à une autre humanité naissante dont nous sommes les descendants.

Eléments repris du film précédent

Le reste du film BAM - Bâtisseur de l'Ancien Monde présente encore quelques sujets qui étaient déjà présents dans La révélation des Pyramides, notamment les dimensions de la grande pyramide de Gizeh et de sa chambre haute en granite d'Assouan. On retrouve toute une géométrie basée sur le nombre d'or. (et pi) Ce qui évidement fait ressortir des relations dans tout les sens en proportion. De plus, au de là de la proportion, la dimension de la pyramide et de sa chambre haute est réalisée pour faire des relations qui ne fonctionnent qu'avec la connaissance du mètre !

Le style granite bien poli et géométrie parfaite fait évidemment tout de suite penser à une parenté avec de nombreux autres sites. Ces derniers étant souvent alignés sur un grand cercle (appelée équateur penché dans LRDP), et placés sur des zones sismiques.

Ensuite, on revient sur l'ile de Pâques qui présente une géométrie tout à fait singulière. On dirait bien qu'il y a une construction de l'ile basée sur une géométrie liée au nombre d'or ! (toute géométrie liée à un pentagone, et donc aussi à une étoile à 5 branches donne naturellement des relations liées au nombre d'or)

Le centre même du triangle formé entre les 3 principaux volcans est à une distance de 16180km de la grande pyramide de Gizeh !!! (1.618 étant le nombre d'or)
(Ce fait a déjà fait couler beaucoup d'encre et d'octets.. mais il semble bien que ce soit le cas... )

Personnellement, je n'explique pas comment c'est possible. L'ile serait artificielle ? où alors il y a des effets naturels qui font que le nombre d'or se retrouve partout.... même dans l'émergence d'iles !?

On retrouve bien le nombre d'or en phyllotaxie (arrangement des feuilles, etc...)... pourquoi pas en géologie ?

Voilà donc l'état actuel de mes notes... je vais peut être compléter au fil des interactions avec les visiteurs. N'hésite pas à mettre de commentaires.

Et n'oublie pas d'aller voir le film BAM - Bâtisseurs de l'Ancien Monde....... en Streaming c'est ici en.... Ça en vaut la peine. C'est plein de magnifiques images, et la musique est géniale 🙂

Et voici le site officiel du film BAM: bam-investigation.com (Il y a de nombreuses heures de bonus passionnants !)

Pour aller plus loin....

... Pour prendre la pilule rouge et entrer dans le terrier du lapin blanc....
... Je te donne rendez vous sur le wiki du CRAC... le Centre de Recherche sur les Anciennes Civilisations...... C'est un bloc note qui vise à faire la synthèse de nombreuses, observations dérangeantes, d'hypothèses et de théories pour explorer les mystères du monde.....