comprenons la croissance avant la décroissance

<- retour au sommaire: La décroissance, un nouveau projet de société

L'origine du concept de décroissance

Nicholas Georgescu-Roegen était un économiste mathématicien. Il a remarqué que les économistes se basent sur un modèle économique fondé sur le paradigme de la mécanique newtonienne et ne prennent pas en compte le principe de la dégradation de l'énergie et de la matière. Il a créé un modèle économique qui tient compte de la thermodynamique en introduisant le second principe de la thermodynamique: l'entropie.

L'entropie est ce qui fait qu'un glaçon qui fond dans un verre ne pourra jamais redevenir un glaçon. L'entropie dégrade l'énergie et la matière.

Nicholas Georgescu-Roegen a montré que le moteur de l'économie est en fait très concrètement un moteur thermique.  (si l'on prend en considération que l'industrie fonctionne grâce à la combustion du charbon, puis du gaz, du pétrole, de la fission nucléaire, etc..)

Donc l'économie est une énorme machine thermique qui évidemment dépend des lois de la  physique thermique. Il dresse un constat alarmant: il faut intégrer l'environnement dans le calcul du fonctionnement de l'économie. Sinon on court à la catastrophe ! Il ne faut pas gaspiller nos ressources, l'entropie va s'en charger assez rapidement.

Le concept de décroissance est donc, à la base, un concept économique.

C'est un concept qui veut éviter le gaspillage des ressources naturelles. Un concept qui critique l'idée d'une croissance économique infinie.

Un slogan que l'on retrouve souvent du côté des partisans de la décroissance:

La croissance n'est pas la solution, c'est le problème !

Une explication du mot décroissance nous dit que dans le mot débourser le préfixe dé signifie "sortir de" sa bourse. Ainsi, selon cette approche, le mot décroissance, signifie: sortir de la croissance.

D'accord, la décroissance veut en finir dur système économique qui érige la croissance en dogme. Mais pour bien comprendre ce que l'on entend par décroissance, il faut déjà comprendre ce que l'on entend par croissance.

Qu'est ce que la croissance ?

La croissance en biologie

La croissance, c'est tout d'abord un terme issue du la croissance en taille des être vivant. Si l'on fouille un peu l'étymologie du mot croissance, on trouve que ce mot vient du latin crescere (« naître, venir à la vie ») qui lui-même est dérivé de Ceres (Cérès, déesse de l'agriculture). (Le nom de Cérès est aussi à l'origine du mot céréales)

Tous les êtres vivants croissent, grandissent en taille, augmentent leur consommation de ressource. Cette croissance peut avoir de nombreuses phases.

Pour un humain, on dit communément que nous grandissons les 20 premières années, puis nous vieillissons pour les pessimistes ou nous murissons pour les optimistes.

La croissance d'une colonie de bactérie est souvent caractérisée par une phase de latence, une phase d'accélération, une phase exponentielle, une phase de décélération, une phase stationnaire, une phase de déclin. Tout ce cycle est fortement corrélé avec les ressources à disposition et à la vitesse à laquelle les ressources sont transformées en déchets.

Avec ces exemples, on observe que le terme de croissance peut représenter plusieurs phases, plusieurs sorte de croissance.

Observons du coté mathématique quelles sont ces différentes sortes de croissance.

La croissance en mathématiques

En mathématiques, et surtout en analyse, on étudie des fonctions. On entre une valeur x dans une fonction et on en ressort une valeur y. Une fonction peut être représentée de manière graphique. Ce qui est en général plus parlant.

Nous allons nous intéresser ici aux fonctions avec une croissance positive. C'est à dire des fonctions dont la pente (que l'on peut observer sur un graphe) a une évolution toujours positive.

Il existe plusieurs sortes de fonctions croissantes dont la pente varie plus ou moins vite, qui croissent plus ou moins vite. Si l'on fait un tour des principaux types de fonctions croissantes. On trouve:

• Les fonctions à croissance linéaire. Ex: y=x
• Les fonctions à croissance polynomiale. Ex: y=x²
• Les fonctions à croissance exponentielle. Ex: y= exp(x)

Comme une image est beaucoup plus parlante, voici la représentation des ces types de fonctions en images.

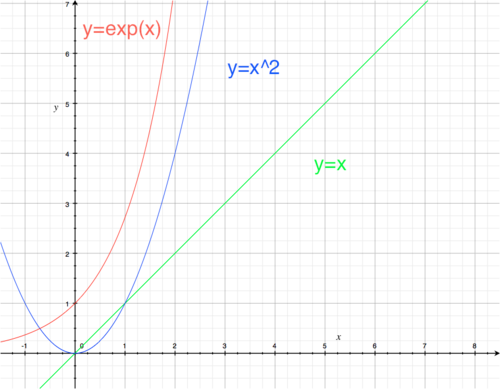
Sur la première image on va se placer proche de l'origine, et observer ses fonctions.

La fonction en vert est une fonction linéaire. y=x. C'est la base de la fonction proportionnelle.

C'est la fonction à laquelle notre cerveau humain est le plus habitué.

De cette fonction on peut faire de nombreuse variantes proportionnelle.s Ici nous avons tout ce qui sort est égale à ce qui entre. On peut créer tout ce qui sort vaut 2 fois ce qui entre. Ou même tout ce qui sort vaut 1000 fois ce qui entre. C'est toujours le même type de fonction. Seule la pente va varier.

En bleu, nous avons la fonction y=x², une fonction polynomiale. Une fonction qui est composée de puissance. Ici nous avons la puissance 2, la fonction "au carré". Tout ce qui sort est ce qui entre multiplié par lui même.

Ce type de fonction est déjà moins intuitif pour notre cerveau humain. C'est ce genre de fonction qui régit les mouvements accéléré et les énergies potentielles mécanique. En d'autre termes quand une voiture a un accident, quand elle frappe un mur ça fait mal. Contrairement à une intuition courante de notre cerveau, ça ne fait pas mal proportionnellement à la vitesse, mais proportionnellement à la vitesse multipliée par elle même !!

Donc ça fait encore plus mal !

En rouge nous avons la fonction exponentielle. En mathématique on dit qu'une fonction exponentielle est une fonction qui est capable de transformer une somme en un produit. Pas très intuitif! C'est une fonction qui est difficile à comprendre pour le cerveau humain.  C'est une fonction qu'il est plus facile de comprendre par des exemples de phénomènes à croissance exponentielle.

Quand on parle de croissance exponentielle, on prend souvent l'exemple de la croissance d'une population.

De plus, exprime souvent la croissance exponentielle sous forme d'un pourcentage : une croissance de 10 % par an signifie que la population est multipliée par 1,1 chaque année. (1/100 = 0.1) Cette valeur en pourcent est un taux de croissance.

De manière générale, on occulte souvent la fonction exponentielle en ne parlant que de taux de croissance. C'est beaucoup plus facile. Car, en ne parlant que du taux de croissance on retombe sur une fonction linéaire. Ce que notre cerveau aime bien !

Mais attention, une fonction exponentielle qui a un taux de croissance constant est toujours en pleine croissance !

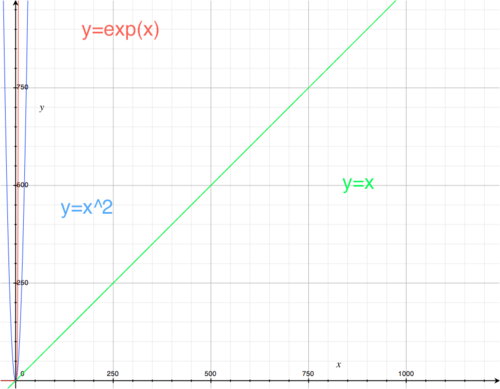
En observant les deux graphes ci-dessus, on remarque, que proche de l'origine, les trois types de fonctions n'ont pas beaucoup de différences. Puis sur le second graphe, on voit mieux que la croissance d'une fonction exponentielle est très différente de celle d'une fonction linéaire.

L'exponentielle a une pente tellement raide qu'il est difficile de la représenter sur un graphe. Mais on peut tenter de concrétiser un peu plus la taille qu'aurait le graphe pour représenter une exponentielle.

On va se dire que l'unité utilisée sur ces graphes est le centimètre. Ainsi, pour un déplacement de 10cm sur l'axe des x, avec ma fonction linéaire y=x j'obtiens un déplacement vertical de 10cm.

Avec la fonction exponentielle, un déplacement de 10cm sur l'axe des x correspond à un déplacement de 22026 cm, soit 220m !!

Si je pousse ne serait ce que de 1cm sur l'axe des x pour arriver à 11cm, j'arriverai à une hauteur de 598,74 m ! et si je vais à 12cm, j'arriverai à 1,627 km

Vu que j'ai encore de la place sur mon axe des x, je pousse un plus loin pour aller me poser précisément à 24,36cm. Quelle est la distance que j'obtiens sur mon axe des y ? .... et bien j'ai choisi cet endroit précis, car on arrive sur la distance qu'il y a entre la terre et la lune ! Soit environ 380 000 km !

Donc il faut se méfier des phénomènes à croissance exponentielle, ils sortent souvent du cadre de l'entendement de notre cerveau humain. Surtout si en plus on masque la croissance exponentielle en parlant de taux de croissance en pour-cent.

Si l'on reprend l'exemple cité ci-dessus, de la population qui augmente de 10% par an. Pour une population de 1000 personnes:

• au bout d'un an, la population vaut 1100 personnes. (1.1 x 1000)
• au bout de 2 ans, la population vaut 1210 personnes. (1.1 x 1100 ou 1000 x 1.1 x 1.1 ou 1000 x 1.1²)
• au bout de 7 ans, la population vaut 1948,717 personnes, soit presque le double. (1000 x 1.1⁷ )
• au bout de 20 ans, la population vaut 6727 soit (1000 x 1.1²⁰ )
• au bout d'un siècle, la population de ce petit village de 1000 habitants verra sa population arriver à 13,78 millions d'habitants !

Un des exemples courant de fonction exponentielle que l'on utilise, ce sont les crédits bancaires. Il faut se rendre compte qu'une somme investie peut doubler rapidement !

Avec un intérêt à 3%, il faut 24 ans à une somme pour se dédoubler ! Ce sont des valeurs courante pour des hypothèques !

Donc il faut se rendre compte que la plupart des gens payent plusieurs fois leur maison !

Pour bien comprendre, voici un Jeu de la poste suisse pour apprendre à gérer son budget.

Il y a un calculateur de crédit (feuille xls) pour bien comprendre le fonctionnement des  intérêts.

La croissance en économie

Pour le commun des mortels la croissance économique c'est surtout la petit infos du jour dans les médias.

Voici un exemple de ce que l'on a pu entendre sur la rsr le 2 septembre 2010.

La croissance de l'économie suisse se poursuit, au deuxième trimestre, le produit intérieur brut a progressé de 0.9% par rapport aux trois premiers mois de l'année... (...) ...et puis les services financiers ont le sourire avec une hausse de 1,6%... voilà pour les gagnants, mais tous les secteurs ne connaissent pas une croissance, les services publics n'ont pratiquement pas créés de valeurs....

Voici cet extrait du journal de la rsr au format mp3

On nous dit dans ce journal radio que la croissance du PIB, le Produit Intérieur Brut a augmenté de 0.9% en suisse pendant la durée du dernier trimestre.

Le produit intérieur brut est un indicateur qui renseigne sur la valeur de l'accroissement des richesses. Quand on nous parle de la croissance du PIB, on nous parle de la croissance d'une croissance.

Il faut se souvenir de la fonction mathématique exponentielle que nous avons vue. Il est possible d'exprimer la pente de la fonction, sa croissance, par une taux en pour-cent. Même si le taux est constant d'une mesure à l'autre, la fonction est toujours une fonction croissante !

Ici on nous indique que le taux de croissance lui même a augmenté de manière croissante. Ainsi on a encore accentué la pente de notre fonction exponentielle. Nous avons un gain qui est énorme, inimaginable pour un cerveau humain.

Cependant la manière dont la croissance du PIB est présentée fausse tout. Si on reproche à une entreprise que sa progression de croissance s'est ralentie, on à l'impression de comprendre que son chiffre d'affaire a baissé. Mais ce n'est pas vrai, il a grandit. Il a même grandit de plus en plus vite. Mais pas aussi vite que ce que certains analystes avaient prévus !

Une valeur en pour-cent n'est qu'une proportion. Le 3% d'une année est forcément plus grand que le 3% de l'année d'avant si l'on refait le calcul en ayant ajouté à la valeur totale la valeur absolue de ce petit bout de 3%.

Ainsi si l'on reprend l'exemple de la population de notre petit village de 1000 habitants.

Si l'on se dit qu'il y a une croissance de 10% de la population les 20 premières années, puis le taux de croissance diminue, on a plus que 8% de croissance les 20 années suivantes, on arrive à une population de:

• au bout de 20 ans, à 10% la population vaut 6727 soit (1000 x 1.1²⁰ )
• au bout de 20 ans de plus, à 8% la population vaut 31354 soit (6727 x 1.08²⁰ )

Malgré la diminution de 2% de taux de croissance, la population à plus que quadruplé les 20 années suivantes !

Une diminution de taux peut donc quand même être de la croissance !

Mais effectivement dans l'absolu la croissance a été un peu moindre que si le taux était resté à 10%

• au bout de 40 ans de plus, à 10% la population vaut 45259 soit (1000 x 1.1⁴⁰ )

C'est ainsi que l'on peut voir que même avec une croissance négative du PIB, il est possible de voir une valeur absolue plus grande !

Quelques exemples de PIB selon la page de wikipedia.. mais la fiabilité n'est pas à toute épreuve !

PIB suisse en millions de $:

2006: 377 240
2007: 415 516
2008: 492 595
2009: 494 622 => -1,45%

On nous dit que la croissance du PIB es négative entre 2008 et 2009 alors qu'en absolu le PIB a augmenté !

USA:

2008: 14 264 600
2009: 14 256 275  => -2,44%

Mauritanie:

2007: 2 644
2009: 3 029 => -1,07%

Monde:

2008: 60 689 812
2009: 57 937 460 => -0,60%

Brésil:

2008: 1 572 839
2009: 1 574 039 => -0,19%

Voici un outil pour comparer l'évolution du PIB en suisse et le comparer à l'évolution du taux de croissance annuel de ce PIB

Source: tradingeconomics.com

Evolution du taux de croissance annuel du PIB

Source: tradingeconomics.com

On peut observer d'une manière globale que le PIB en absolu augmente toujours.

Souvent dans les médias on nous parle uniquement du taux de croissance. Le taux de croissance peut augmenter ou diminuer et ainsi on explique que l'économie va bien ou mal. Que l'on est en boom économique ou en récession.

Mais en fait, globalement, la valeur absolue du PIB est toujours en augmentation, en pleine croissance, et même en croissance de type exponentielle.

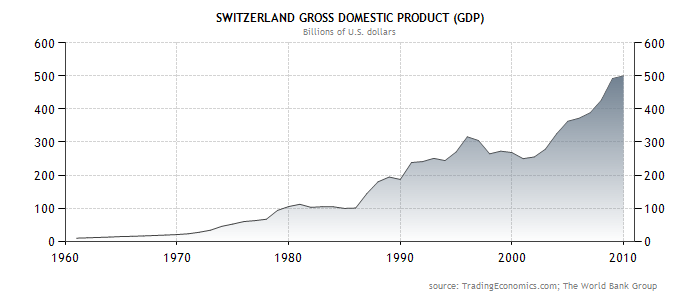
Voici un graphe qui illustre la valeur absolue du PIB suisse en milliard de $ entre 1960 et 2010:

On observe que la valeur absolue de ce PIB a déjà doublée dans les 10 dernières années. En 2001, le PIB suisse était de 250 Milliards de $ et en 2010 le PIB suisse est de 500 Milliards de $.

Il subsiste tout de même un biais dans cette présentation, c'est le fait que l'économie suisse utilise beaucoup sa propre monnaie qu'est le franc suisse, alors que ce graphe est présenté en $ dollars US. Le taux de change entre ces monnaies à pas mal changé en 50 ans. Actuellement, en 2011, 1$ = 0.83 CHF alors qu'en 2001, 1$ = 1.7$.

Par rapport à l'inflation, il semble que le dollars de 2011 vaut 7.5 fois moins qu'en 1960.

Comparé à l'or, le dollar perd 98 % de sa valeur entre 1971 et 2010. L'once d'or est passé en 40 ans de 35 à 1 250 dollars. Ainsi, c'est peut être une partie de cette dévaluation du dollars par rapport au franc et permet de soutenir la croissance !

Mais le problème ne change pas. Le PIB ne fait que d'augmenter, même si le taux de croissance est variable.

Ainsi, à l'avenir, il nous faudra échanger encore plus d'objet et de services pour faire croitre le PIB, donc il faudra encore plus transformer des ressources naturelles en déchêts !

De combien va encore augmenter le PIB ?

Il est impossible de prévoir le futur, mais on peut faire comme les économistes qui aime prévoir le futur par des projections du présent.

Si l'on table sur une croissance du PIB de 2% par an on peut utiliser la formule suivante:

y = 500 (1.02)^x

500, c'est les 500 milliards du PIB suisse en 2010, 1.02, c'est pour dire que l'année suivant, on veut le même résultat augmenté de 0,02 fois, c'est à dire 2% et l'année est la variable x en exposant.

C'est donc bien une équation d'une fonction exponentielle.

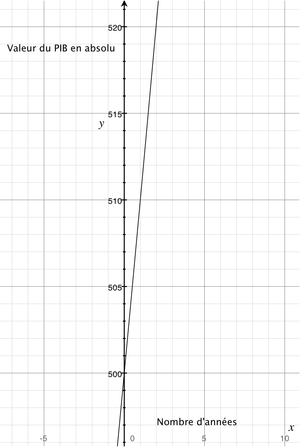
On peut voir sur le graphe ci-contre de cette fonction que le PIB continue d'augmenter très vite. Tellement vite que mon échelle ne me permet d'afficher que les 2 prochaines années où l' on arrive déjà à 520 milliards. Donc, d'ici 2 ans, en plus de ce que l'on consomme maintenant, on consommera aussi l'équivalent de ce qui permettait à l'économie du début des années 1970 de tourner !

Mais ceci n'est qu'une projection du passé sur le futur. Seuls les économistes sont assez fous pour penser que l'on peut ainsi prédire l'avenir. Comme je l'ai déjà expliqué dans un article, l'avenir est imprévisible. Les grands événements qui ont marqué l'histoire étaient totalement imprévus.

Avec une telle croissance de 2%, en 2050, (date pour laquelle on fait beaucoup de projections), on devrait, en suisse consommer 2 fois plus de ressources que maintenant.

Une image vaut mille mots dit-on. Alors, j'ai tenté de montrer graphiquement ma projection de la croissance du PIB suisse pour 2050.

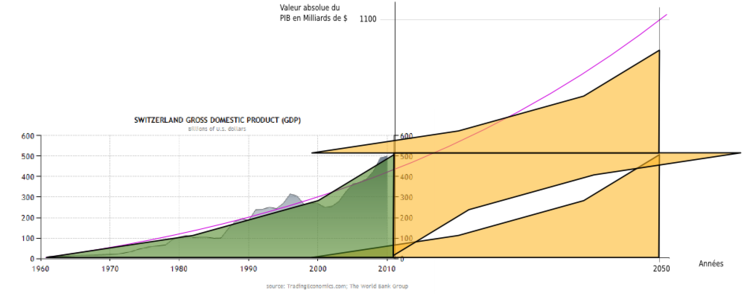
J'ai repris le graphe déjà montré ci-dessus, qui montre la valeur absolue du PIB suisse en milliards de $ depuis 1960 jusqu'en 2010.

La surface sous cette courbe représente tous les services et biens qui ont été consommés pour atteindre cette évolution du PIB. En vert, nous avons tout ce qui a déjà été consommé ces 50 dernières années.

Puis j'ai projeté la courbe jusqu'en 2050. Là, si l'on suppose un PIB de 500 milliards de $ en 2010, avec un croissance annuelle de 2%, en 2050, nous arrivons à un PIB de 1100 milliards.

Pour tenter de me représenter le volume de services et biens qu'il faudra consommer pour atteindre ce PIB de 1100 milliards en 2050, j'ai cloné la surface verte en surface jaune. J'ai rempli tout l'espace à disposition avec des surfaces jaune. (En terme mathématique, calculer la surface sous une courbe revient à calculer l'intégrale de cette fonction.)

J'arrive presque à placer 3 fois cette surface dans l'espace à disposition.

Cela signifie que pour atteindre le PIB qui correspond à une croissance annuelle de 2% jusqu'en 2050, nous aurons besoin de consommer 3 fois plus de services et de biens que ce qui a été produit entre 1960 et 2010.

Avec tous les problèmes de ressources et de dérèglement climatique que l'on observe à l'heure actuelle, ça me semble juste totalement impossible !!!

Il sembée que c'est  Kenneth E. Boulding qui disait:

Celui qui croit qu'une croissance exponentielle peut continuer indéfiniment dans un monde fini est soit un fou, soit un économiste.

Réfléchissez à ce qu'il faut pour mettre en place une telle économie. Comment va ont pouvoir consommer encore plus ?

Une solution est de rendre tout jettable. Diminuer la durée de vie des appareils et augmenter leur nombre. Vous devrez changer votre téléphone tous les 3 mois, votre ordinateur chaque année, vos habits chaque semaine. Vous mangerez uniquement de la nourriture qui vient de l'autre côté de la planète pour qu'un maximum d'intermédiaires aient pu la toucher, vous n'aurez plus de vaisselle autre que de la vaisselle jettable.

Il faudra privatiser totalement l'espace public. Chaque rue sera payante, le GPS que vous avez toujours sur vous enregistrera votre parcours et permettra à la fin du mois de vous facturer uniquement les trajets que vous avez effectué.

- Restez chez vous et vous ne payerez rien dira la pub des livreurs à domicile.

L'école publique est une charge, on va la privatiser, ainsi elle peut rentrer dans le calcul du PIB, passer de charge à profit !

Dans la même logique, les crèches seront obligatoires. Un parent qui reste à la maison s'occuper de son enfant est un parent qui ne crée pas de valeur ! Un parent qui reste à la maison s'occuper de son enfant est une place de travail de moins dans une crèche !

En bref, on doit étendre la sphère marchande et faire tourner plus vite le circuit économique.

Comment est calculé le PIB ?

Le PIB est un indice qui est construit avec de nombreuses règles. Il y a des choses que l'on comptabilise dans les richesses et d'autres que l'on ne comptabilise pas.

Quand on entend dans le journal de la RSR que les services financiers sourient mais que les services publics n'ont pratiquement pas créés de valeurs, il faut réfléchir un peu.

Le PIB tient compte des gains en bourse, mais il ne tiens pas compte de ce que l'Etat dépense pour financer les écoles.

Autrement dit, pour augmenter le PIB, on devrait ne plus fiancer les écoles et immobiliser tout l'argent ainsi économisé en le plaçant en bourse ! Logique !

De même, les catastrophes sont toujours bonne pour augmenter le PIB. Un accident de voiture fera travailler de nombreuses personnes, des ambulanciers aux vendeurs de ferraille pour l'épave et de voiture pour le remplacement.

La pollution d'une rivière par une usine sera bénéfique pour le PIB, l'entreprise produira à moindre coût si elle n'as pas besoin de filtre anti-pollution pou rejeter son poison. Il faudra de nombreux spécialiste pour étudier la catastrophe et finalement d'énormes travaux pour assainir la pollution !

Si le moteur d'une voiture à l'arrêt dans un embouteillage tourne, ça fait augmenter le PIB. Il faudra m'expliquer où se trouve la création de richesse dans tout ces exemples !

Donc souvent une perte de patrimoine, de vie humaine, de ressources naturelles est comptabilisé comme une richesse !

Par contre l'école, à moins qu'elle soit privée et donc non financée par l'Etat, ne crée jamais aucune richesse. Pire, elle dilapide de l'argent !

Finalement, je me demande vraiment pourquoi les médias nous bassinent autant avec la croissance du PIB ?

D'autres indicateurs économiques

Parfois, il faut savoir changer de lunettes. Garder l'esprit ouvert. Voir qu'il existe de nombreux autres indicateurs économiques que le PIB.

Parmi cette foultitude d'indicateurs économique. On peut s'arrêter sur l'indice de santé sociale, qui comme son nom l'indique prend en compte des questions de sociales et de santé.

Cette indice, contrairement au PIB, comptabilise les accidents de la route comme un drame et nom comme un bienfait. Ce qui semble assez logique.

Voici une comparaison entre l'indice de santé sociale et le PIB américain entre 1959 et 1996:

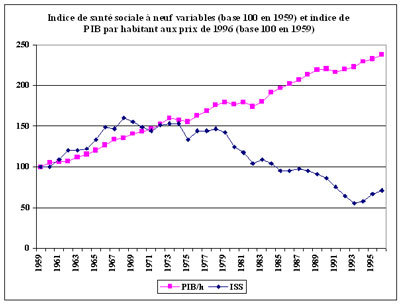On remarque un découplage de ces indices aux environs de 1975.

Depuis le milieu des années 1970, la croissance du PIB n'est pas un signe de croissance du bien être comme c'était le cas auparavant.

Voici encore un autre indicateur économique, l'indicateur de progrès véritable.

Cet indicateur est semblable au PIB, mais il prend en compte également la création de richesse qui ne passe pas par une monétisation comme le bénévolat ou le travail domestique.

De plus, il a une composante écologique qui déduit de la création de richesse, les pertes écologiques et les dégâts sociaux.

Voici une comparaison entre le PIB et de l'indicateur de progrès véritable des années 1950 à la fin des années 1990:On observe que les courbes se découplent vers le début des années 1970. Le progrès véritables stagne, voir diminue quand le PIB croit.

Ainsi on observe que les outils mis en place à la fin de la deuxième guerre mondiale pour évaluer notre économie ne sont pas forcément tout à fait adaptés.

Cela fait 50 ans que nous avons des outils alternatifs pour voir une réalité tout autre que la croissance du PIB comme source de bien être. Pourquoi est ce que l'on garde le PIB comme référence majeure ?

Pourquoi est-ce que les médias nous parlent toujours du PIB dans le flash info et très rarement de la cinquantaines d'autres indicateurs économiques ?

Les choses bougent quand même. Il existe des initiatives du genre de la commission Stiglitz, qui ont pour but de définir de nouveaux indicateurs de richesse plus juste.

Mais finalement, on les a pas déjà ces indicateurs ?

Il suffit juste de décider de ce qui a le plus d'importance dans nos valeurs.... pour le moment, d'après les médias et politiques du moment, on dirait que seul le PIB compte.....

Suite => La publicité, le moteur du consumérisme