Sur le net on trouve de tout et n'importe quoi sur les pyramides de Gizeh en Egypte. C'est un sujet mystérieux qui passionne les foules depuis des millénaires. (si si... des millénaires.. j'aime bien relire des vieux livres... et en fait "rien de nouveau sous le soleil"..)
Si on lit des anciens livres on trouve des questionnements identiques chez nos ancêtre que de nos jours. J'ai même l'impression parfois, qu'on en savait plus il y a longtemps que de nos jours ! (par exemple en lisant les livres de Jomard, un des tout premiers égyptologues qui a fait la campagne Napoléonienne de 1798 )
Je suis moi même passionné du "mystère des pyramides"... un "pyramidiot" selon les ignorants qui pensent déjà tout savoir....

J'ai déjà publié pas mal d'articles sur quelques idées liées aux pyramides. Notamment mes recherches sur la géométrie sacrée.... sur les pierres moulées géopolymères....
Aujourd'hui voici un nouvel élément qui, je le trouve, mérite d'être diffusé:
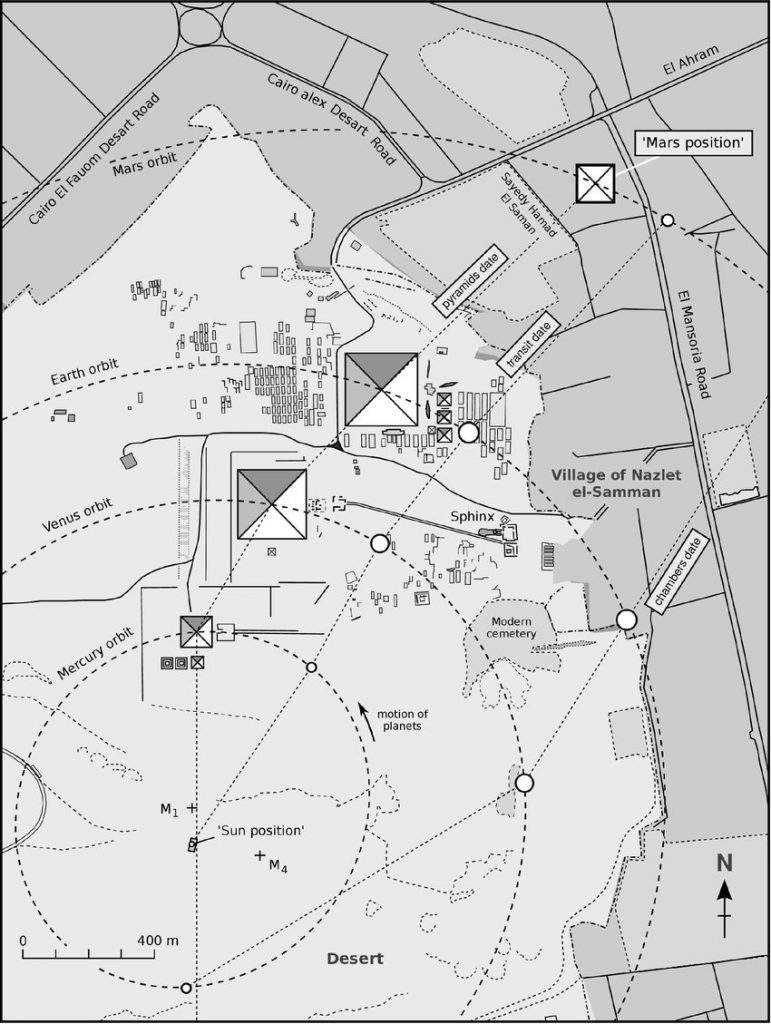
Le plateau de Gizeh est un gigantesque planétarium et les pyramides représentent les planètes du système solaire.
Le planétarium de Gizeh
Bien que rétrospectivement j'ai déjà entendu plusieurs idées et faits qui vont dans le sens que les pyramides sont des représentations des planètes. Ce n'est que lors de ma découverte de cette vidéo que "tout s'est éclairci dans mon esprit".
Il semble que cette vidéo n'est pas disponible à l'intégration... mais va la voir sur youtube....
Il y 3 points majeurs:
- les pyramides symbolisent les planètes du système solaire
- les pyramides sont placées sur les orbites moyenne des planètes à une échelle de 100 millionième
- les pyramides ont des tailles apparentes vues depuis le lieu symbolisant le soleil qui sont en relation avec leur magnitude apparente.
Les pyramides symbolisent les planètes du système solaire
Voici la liste que je vois avec la vidéo ci-dessus et mes propres recherches.
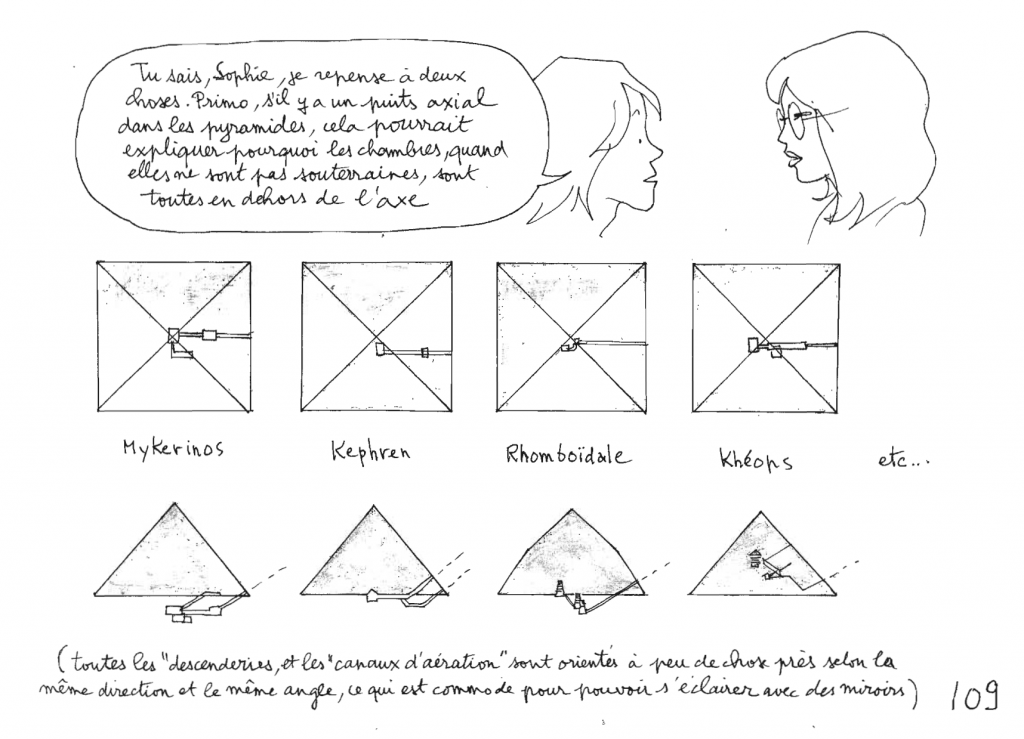
- Mercure → Mykérinos
- Venus → Khéphren
- Terre → Khéops
- Mars → ? (ou la bande de granite rouge de Mykérinos)
- (Cerès) →
- Jupiter → Djédéfrê
- Saturne → Djéser (Libations des divinités)
- ? Pyramide rouge (la brillante) + rhomboïdale (celle qui brille au sud)
- Uranus → ?
- Neptune → ?
- (Pluton: la "fausse planète") → Meïdoum.. (la "fausse" pyramide)
... et que faire des autres pyramides ?
J'ai regardé la liste des pyramides d'égypte. ... il y en a beaucoup !
(comme les astres !...)
Est-ce que les pyramides satellites sont des satellites de planètes ?

Aperçu de dessus de ce planétarium de Gizeh:
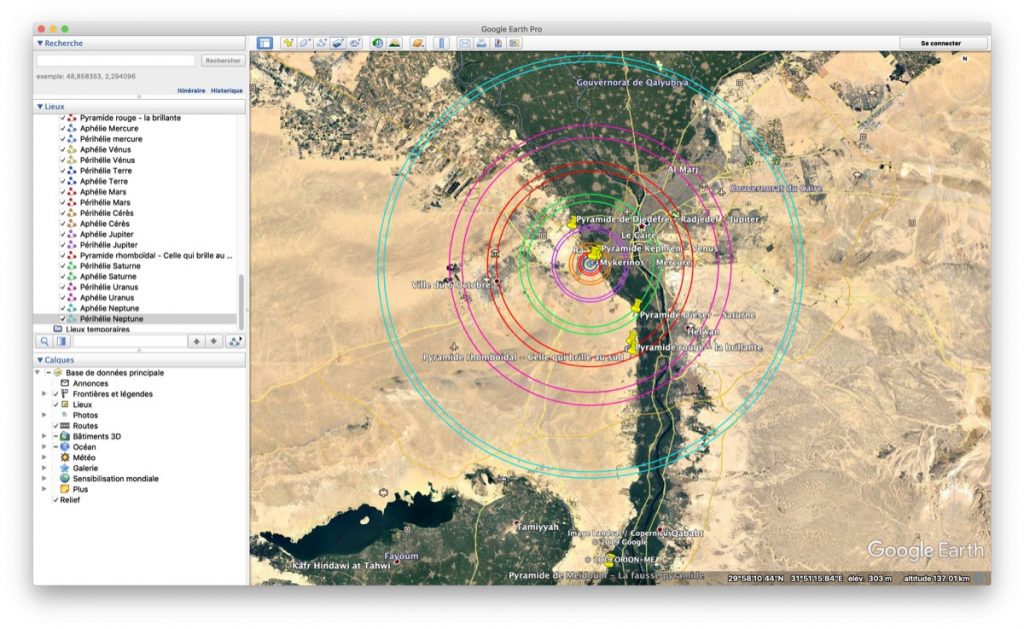
"Ce qui est en bas est comme ce qui est en haut, et ce qui est en haut est comme ce qui est en bas" Table d'émeraude d'Hermès Trismégiste.
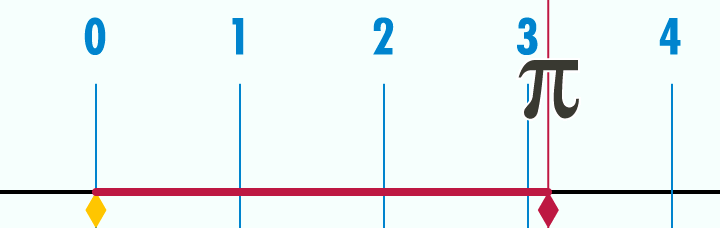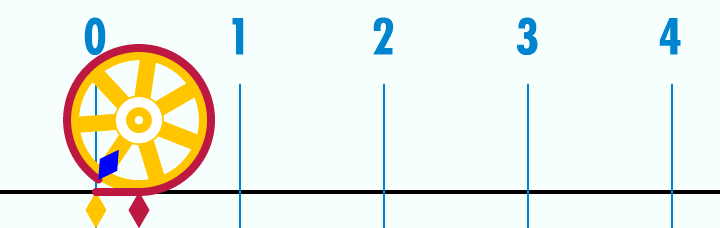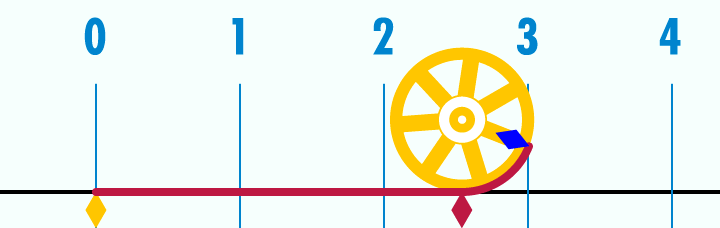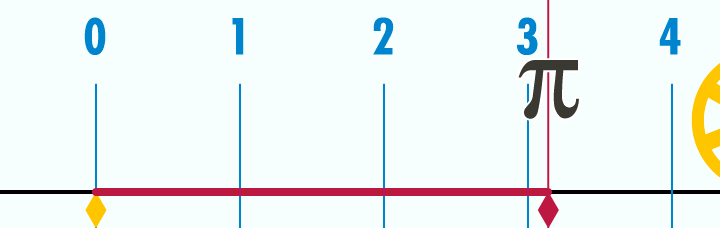
Les pyramides sont placées sur une orbite moyenne des planètes à l'échelle 1: 100 millionième
Voici un aperçu des orbites moyennes (donc périhélie + aphélie) pour chaque planète. Avec aussi les marqueurs des pyramides principales.
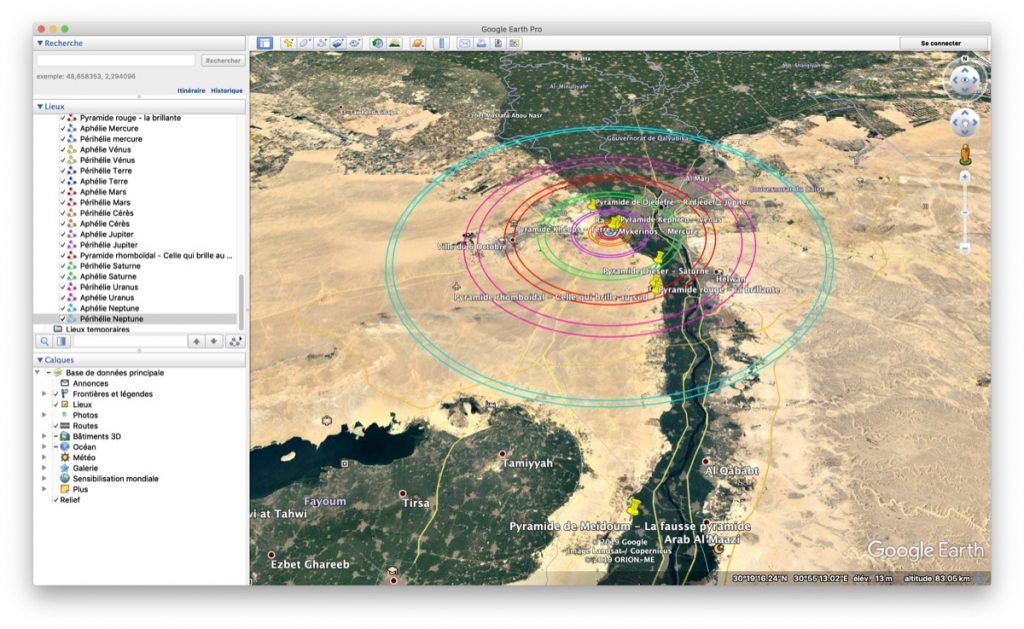

La taille des pyramides est en fonction des magnitudes apparentes des planètes depuis le soleil
Ce n'est pas la taille absolue de la pyramide qui compte. Mais la taille vue depuis le soleil (le point de vue touristique). Donc la magnitude apparente.
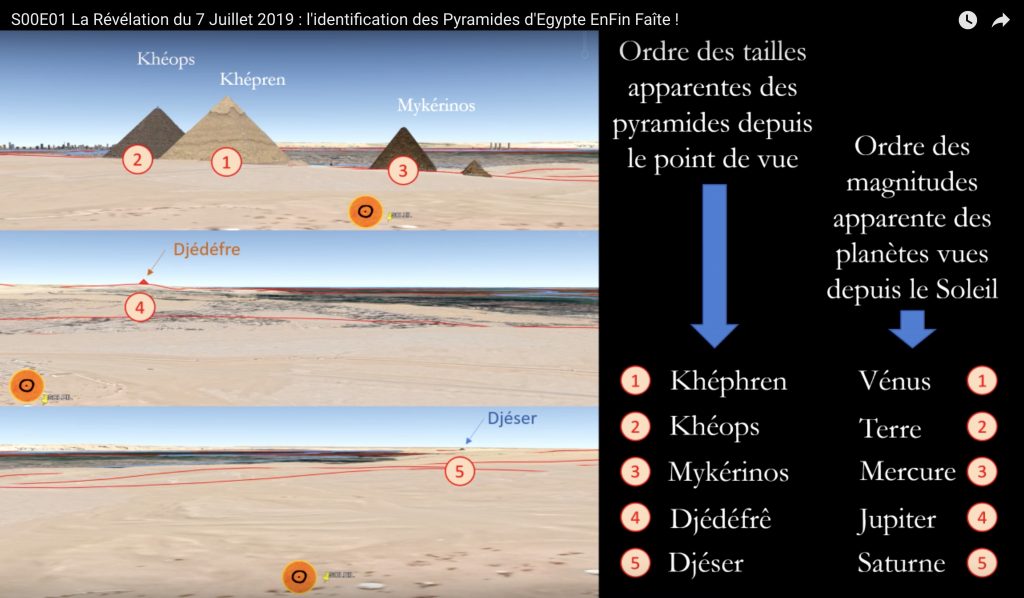
Vérifie par toi même le planétarium de Gizeh sur google earth
Alors après avoir vu cette vidéo, j'ai voulu vérifier.
J'ai refait les mesure sur google earth.
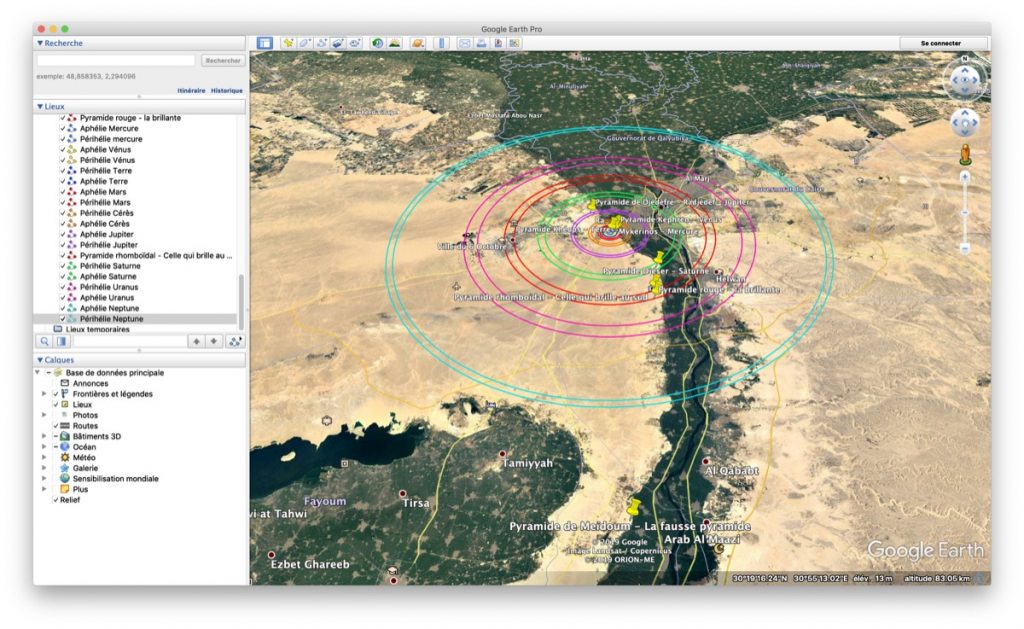
J'ai repris les distances des planètes aphélie et périhélie sur wikipedia. Voici aussi un autre site qui donne les distances des planètes au soleil.
J'ai regardé la liste des pyramides d'égypte.
Et j'ai refait un fichier kml que tu peux reprendre ici.
J'ai mis les périhélies et aphélies de toutes les planètes.
Je trouve que c'est très harmonieux !!
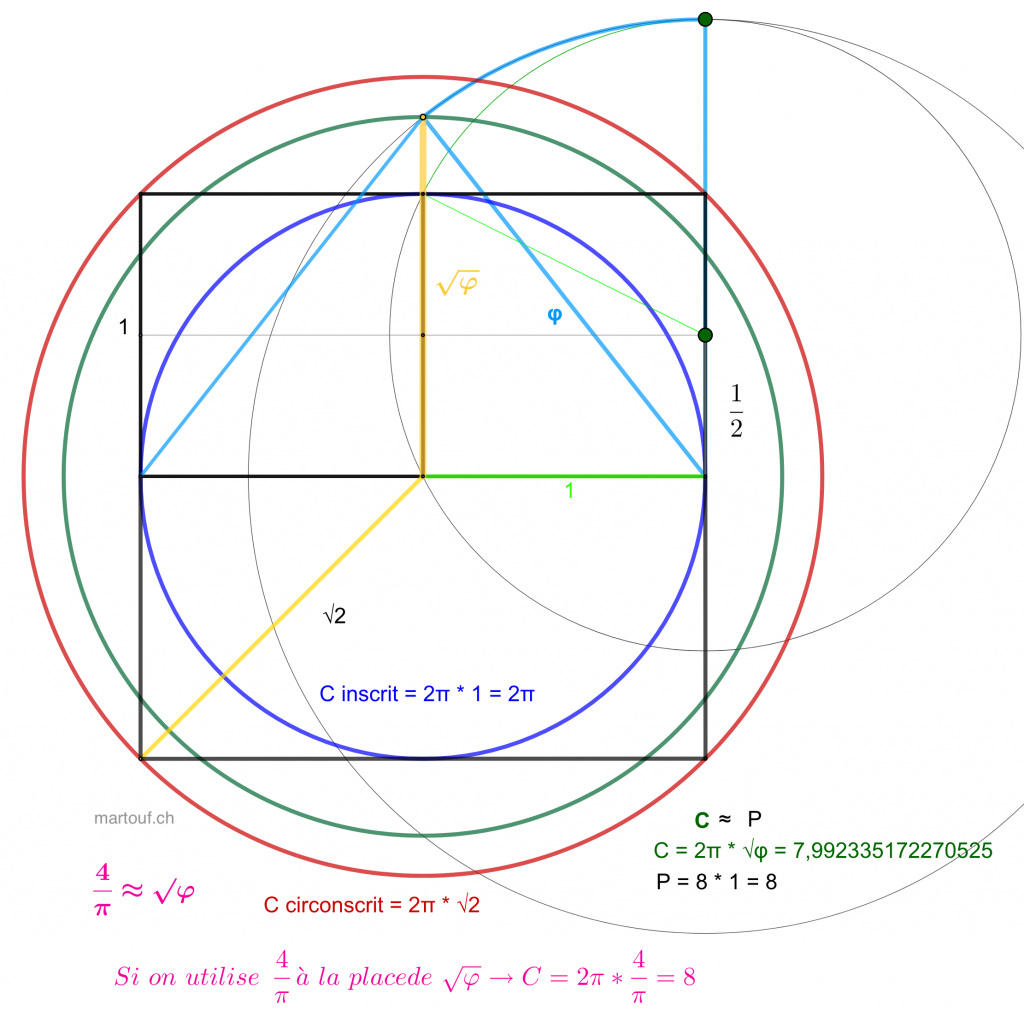
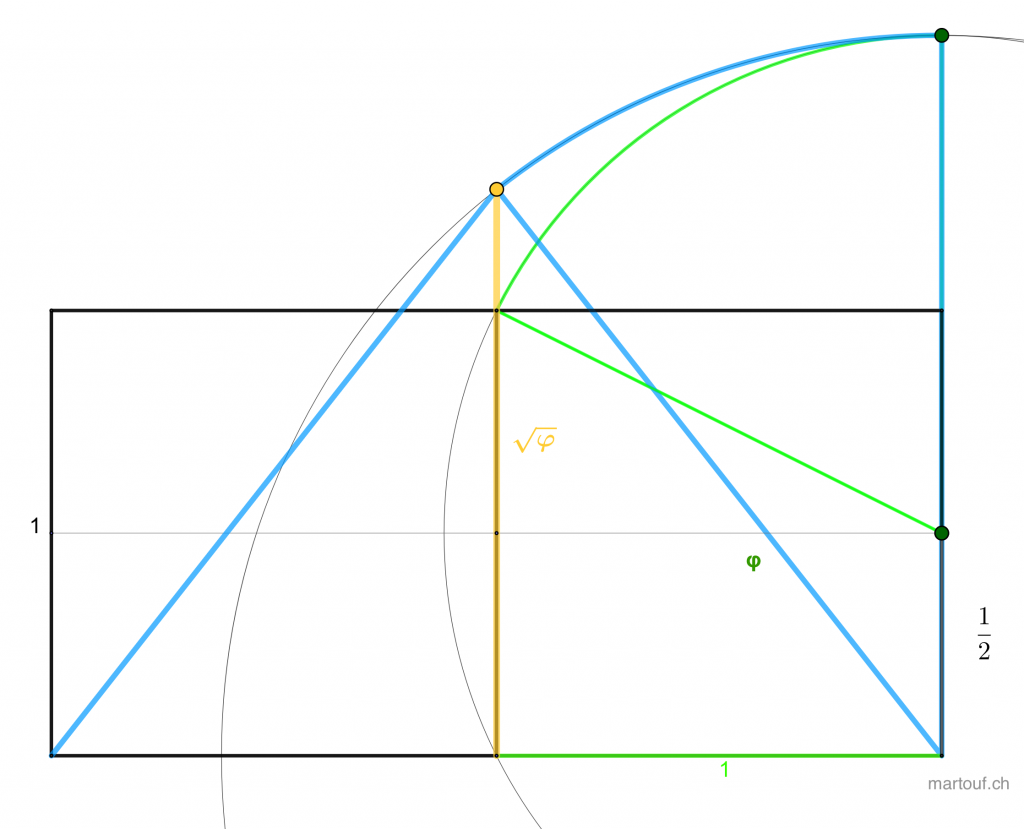
Il y a certainement une géométrie liée au nombre d'or… ou a son approximation, la suite de fibonacci.... comme l'avait montré Souriau ...
Pour vraiment compléter l'harmonie, j'ai du inclure l'orbite de cérès. Cérès est la planète naine, le plus gros objet de la ceinture d'astéroide.
Pour moi ça complète la vision d'Anton Parks avec la grosse planète Mulge qui était à cet endroit, puis elle a été détruite et son satellite Mulge-tab a été éjecté de son orbite… s'est baladé comme une comète pendant 900 ans… et a fini par se stabiliser sous la forme de Vénus.
J'ai également complété avec les planètes plus lointaines, jupiter, saturne, uranus, neptune.
C'est harmonieux.
Ensuite j'ai aussi vérifié l'ancienne "planète" pluton. J'ai vu avec amusement que l'orbite plausible de pluton la "fausse" planète correspond à l'emplacement de la pyramide de meidoum…. la "fausse" pyramide !!!!
Incroyable !!
Il y a aussi un truc étonnant. C'est la pyramide rouge et la pyramide romboïdale. Elles sont exactement sur le tracé aphélie et périhélie d'une planète placée harmonieusement……..
Mais quelle planète ?? J'ai pas trouvé… J'en déduis qu'il y a un emplacement pour une planète entre saturne et uranus.
Le nom de ces pyramides est aussi révélateur qu'elles vont ensemble.
Leur nom sont:
- La brillante (pyramide rouge)
- Celle qui brille au sud (pyramide romboïdale)
Il y a cette idée de "briller"….
"Le brillant" est un des surnom d'Osiris.
Mais ou est mars ?
Il y a 2 théories. Soit la pyramide a disparue.... (elle était pas si grosse vu la magnitude apparente)
Soit une seule pyramide symbolise deux planètes... c'est l'idée qu'à eu Fred dans un second temps..
La bande rouge de la base de la pyramide de Mykerinos symbolise la planète rouge.

Cette théorie et bien d'autres est développée dans cette vidéo...
Une publication d'un physicien qui va dans le même sens
Hans Jelitto, un physicien allemand a fait une publication scientifique pour montrer la corrélation entre les 3 premières planètes du système solaire et les 3 premières pyramides.
La publication est disponible ici.....

Par contre le point de vue du soleil, n'est pas le même !! ... mais c'est un des deux possibles en croisant les orbites des 3 premières planètes/pyramides. Un choix différent... mais une démarche similaire !
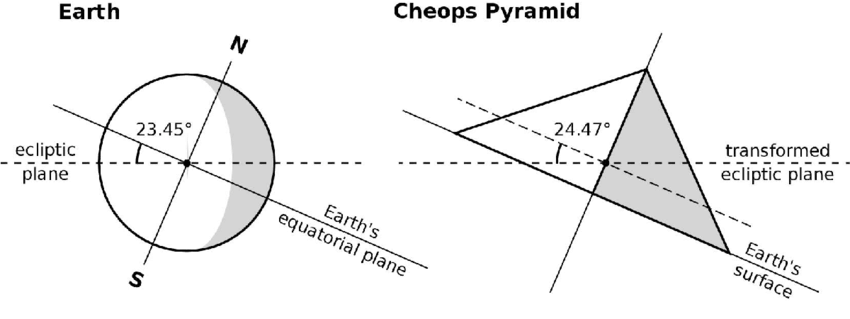
Il y a aussi l'idée de l'inclinaison que Fred n'a pas. Mais qui joue aussi !!!
Ceci en rapport avec l'inclinaison de l'axe de la terre.
Des légendes anciennes qui disent que la grande pyramide contient des informations sur la Terre
Il n'est pas nouveau que la grande pyramide de Gizeh soit associée à des informations astronomiques et géographiques.
Le calife Al-Mamoun
Au 9ème siècle, le calife Al-Mamoun s'intéressait beaucoup à la cartographie. Son ambition était de calculer la circonférence de la Terre.
Il a envoyé des scientifiques, des arpenteurs avec des astrolabes, des baguettes d'arpentage et des cordes pour mesurer la circonférence de la Terre en se basant sur l'étoile polaire. Il ont trouvé 37 000 km. (on est à 40 000)
Dans un documentaire passé à la TV sur la grande pyramide de Gizeh, j'ai vu passer une info qui m'a fait tilt ! ... parmi le bourrage de crâne incohérent des explications "officielles" il y a quand même parfois des perles.
L'info, c'était que le calife Al-Mamoun, dont ont dit qu'il a fait creuser en 832, l'entrée utilisée actuellement par les touristes, cherchait des trésors dans la grandes pyramide. L'histoire s'arrête souvent là.
Mais ici, l'égyptologue Salima Ikram nous explique que Al Mamoun ne cherchait pas n'importe quel trésor... mais des cartes du monde et des objets magiques.
Donc pour moi Al-Mamoun n'était pas un "bête" pilleur de tombe comme on le dit souvent. Mais sa quête scientifique de mesurer la Terre l'a amené à penser que dans la grande pyramide il y avait des cartes du monde. D'où vient cette idée ?
Le documentaire nous dit que ça vient du papyrus Westcar un papyrus du temps de la XVIIème dynastie qui parle des prodiges magiques des rois des premières dynasties, donc les prodiges de Khéops et les salles se secrètes du temple de Thot qui renferment toutes la connaissance du monde. (du coup la grande pyramide n'est pas le tombeau de Kheops.. mais le temple de Thot !!)
Du coup, Al-Mamoun a été très déçu, car après après avoir passé des mois à faire creuser une entrée, en chauffant la pierre et en la faisant éclater en jetant dessus du vinaigre, il n'a trouvé que des chambres vides....
En fait, c'était ne pas comprendre que c'est la géométrie de la pyramide elle même qui est la carte !!!
Au passage je profite de souligner que le calife Al-Mamoun était quand même très chanceux d'avoir passé des mois à creuser "au hasard" et de tomber pile poil sur le croisement de la grande galerie avec la galerie descendante !
Sachant que le périmètre de la grande pyramide fait 920m.... d'avoir choisi sur le bon endroit, et la bonne hauteur me semble pas du tout le fruit du hasard. Mais ça ça ne semble jamais intéresser les égyptologues des documentaires TV.... seulement les "pyramidiots".... qui sont les idiots ?
Pour moi peut être même que cette "entrée" est en fait une "sortie". Car logiquement il est beaucoup plus simple de partir des couloirs de la pyramide et de creuser un chemin qui va déboucher à l'extérieur !
Peut être que c'est juste l'agrandissement par Al-Mamoun d'un fin passage... d'un conduit qui était à ce niveau ?
Cette piste de l'agrandissement est intéressante car un texte arabe ancien semble aller dans ce sens. Le calife n'étant resté que 49 jours dans la région. Il devait aller vite. (donc pourquoi le documentaire dit que Al-Mamoun a creusé DES mois ? .. ça en fait même pas 2 !)
Murtada Ibn al-Khafîf a écrit sur l'entrée dite d'al-Ma'moun, de la Grande Pyramide : "Le Commandeur des Fidèles le Mamune [al-Ma'moun], Dieu lui fasse miséricorde, étant entré dans le pays d'Égypte, et ayant vu les Pyramides, eut envie de les démolir , pour le moins quelqu'une d'elles, afin de savoir ce qui était dedans. Sur quoi on lui parla ainsi : Vous désirez une chose qui ne vous est pas possible. Si vous l'entreprenez et que vous n'en veniez pas à bout, ce sera une honte au Commandeur des Fidèles. À quoi il répondit : Je ne puis me passer d'en découvrir quelque chose. Il fit donc travailler à la brèche qui y était déjà commencée, et y fit de grandes dépenses."
.... la brèche était déjà là.... Mais d'où vient elle ?
Newton veut faire valider sa théorie de la gravité en se basant sur les mesure de la grande pyramide
Le physicien (et alchimiste) Newton avait besoin d'une mesure précise de la Terre pour affiner sa théorie de la gravité. Il pensait pouvoir retrouver la taille d'un degré de méridien en fonction d'une mesure ancienne égyptienne encodée dans la dimension de la grande pyramide de Giezh. (voir aussi sa dissertation sur le unités de mesure anciennes)
Il a voulu utiliser les mesures de l'astronome anglais John Greaves, un passionné d'unités de mesure antiques qui a visité la pyramide en 1638.
Mais ça ne semblait pas suffire. Newton a aussi compté sur les mesure du savant italien Burattini, qui a vécu en égypte entre 1637 et 1641 et y a mesuré la pyramide.
En 1675, Burattini publie Misura Universale, ouvrage dans lequel il renomme la mesure universelle de Wilkins en mètre universel « metro cattolico » (qui signifie "mesure universelle") et la redéfinit comme étant la longueur d'un pendule qui oscille avec une demi-période d'une seconde, soit environ 993,9 mm actuels.
(au passage, la théorie de la gravité n'était pas connue... vu que Newton ne l'avait pas finalisée... mais le mouvement du pendule dépend de la gravité et donc de la latitude du lieu.... et là je t'invite à voir ce qu'il se passe si tu te places au pôle.... avec quelle valeur, on va dire... emblématique.... on simplifie la formule ... et ce que ça peut signifier comme définition du mètre ! A mon avis on avait là la véritable valeur du mètre, le st-graal de générations de chercheurs.. un mètre en lien avec la terre et avec la géométrie sacrée. ... et on découvre que notre version du mètre est fausse... que la version provisoire était plus juste que la version définitive.... Je ferai un article là dessus un jour... mais d'abord je vais te laisser chercher... :p )
Mais finalement Newton a utilisé les travaux de Jean Picard qui a mesuré en 1669-1671 un degré de méridien. Et du coup on a eu pour la première fois depuis Eratosthène une mesure de la circonférence de la Terre un peu plus juste.
Dommage que Newton ne connaissait pas les renfoncements des 8 faces de la grande pyramide... c'est justement ce qui montre le taux d'aplatissement de l'éllispsoïde qu'est la Terre.. et ce que Newton cherchait... (une idée.... au passage... à vérifier pour toi qui aime les énigmes... 😉 )
Edmée Jomard et la campagne Napoléonienne
Plus je creuse cette histoire, plus en fait, l'origine du mètre est en fait liée à une reprise d'une unité de mesure (ou d'un dérivé) déjà présente dans l'égypte antique. C'est important ce lien avec le mètre, car dans ce planétarium de Gizeh on voit que l'échelle est en mètre !!!
C'est fou le nombre de savants liés à l'histoire de la métrologie et notamment de la définition et la mesure du mètre utilisé actuellement qui sont allés en égypte ! ... et on nous le dit jamais dans les manuels scolaires !
Pour moi le cas le plus emblématique est Edmée Jomard.
Il dit dans son Mémoire sur le système métrique des anciens égyptiens… :
" Mais le périmètre de la grande pyramide de Memphis avoit 30 secondes du degré propre à l’Egypte, autrement cinq stades compris chacun 600 fois dans ce même degré: l’apothème avoit un stade; le côté, 500" .
La longueur du degré du méridien propre à l’égypte (30° de latitude) mesure 110852.4248 m. Si on divise cette longueur par 120 on obtient 923.8m pour le périmètre de la pyramide, soit 230.942 m pour un côté.
Ce qui à une coudée près correspond aux 440 coudées officiellement admises. (mais avec de grandes variations suivants les auteurs !) La différence s’explique probablement à savoir si l’on prend en compte le socle de la pyramide où non !
L'enquête continue....
Une nouvelle vidéo pour parler de tout ça...
Pendant ce temps à Theotihacan...
... ah et.. oui... j'oubliais la promesse faite dans mon titre accrocheur... si les pyramides d'égypte sont un planétarium... ça semble aussi fonctionner à Teotihuacan..... d'ailleurs là bas, c'est encore plus explicite vu qu'il y a officiellement la "pyramide du soleil" et la "pyramide de la lune"..... mais tout reste à vérifier.
Les pyramides de Teotihuacan sont un planétarium.....
Bon.. et bien garde l'esprit ouvert…. il y a un truc intéressant !!
(et oublie pas de t'abonner à la chaine de l'apprenti-sage qui nous fait découvrir tout ça !!!)