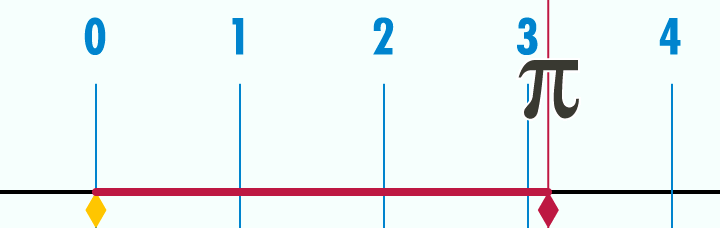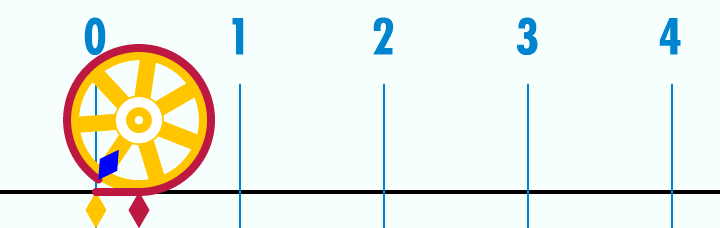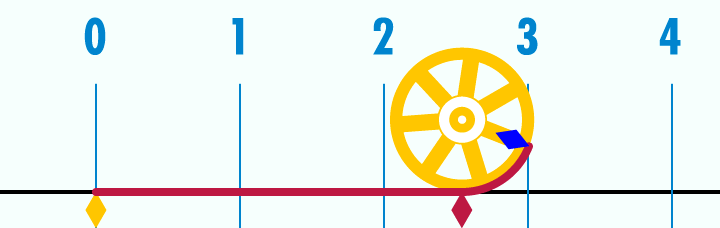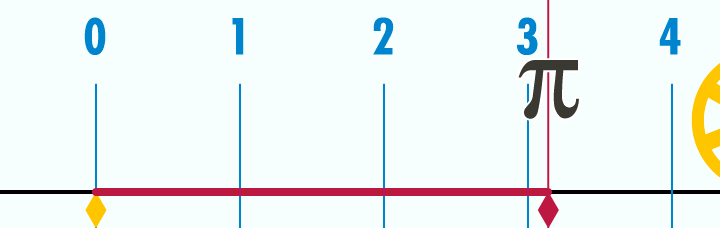
Le mètre est une unité de mesure de longueur qui officiellement a été inventée lors de la révolution française.
La fable nous dit que dans le même ordre d'idée de couper la tête du roi, on se débarrasse des unités de longueurs comme le pied et la coudée par ce qu'on a plus envie d'utiliser des références à l'anatomie d'un roi.
La fable est fausse ! et nie l'évolution de cette idée pendant les siècles précédents
Cette fable est un grand raccourci. Car l'idée d'une unité de mesure universelle était présente avant la révolution, elle faisait partie de demande dans les cahiers de doléance, mais l'idée était bien plus vieille.
Notamment en 1670 Grabriel Mouton proposait d'utiliser la base 10 comme division d'une unité de mesure universelle qu'il appelait virga, (la verge). Cette unité correspond à un millième de la longueur d'une minute d'arc de méridien ~1,8m. (voir mon calculateur pour vérifier)
L'anglais John Wilkins propose à la même période l'adoption d'une mesure universelle (universal measure), d'unités décimales, basée sur le principe d'un pendule battant une seconde, et dont la longueur fondamentale est de 38 pouces prusses (1 prussian inch = 26,15 mm), soit de 993,7 mm (ou 39,25 pouce de Londres). Il publie cette idée en 1668, mais ce n'est que la seconde édition, car tous les exemplaires imprimés de la 1ère ont brulés dans le grand incendie de Londres en 1666.
En 1675, c'est l'italien Tito (Livio) Burattini qui publie un livre nommé "Misura universale" dans lequel il reprend l'idée du pendule comme base universelle d'une mesure universelle. Il traduit "universal measure" par le latin "metro cattolico".
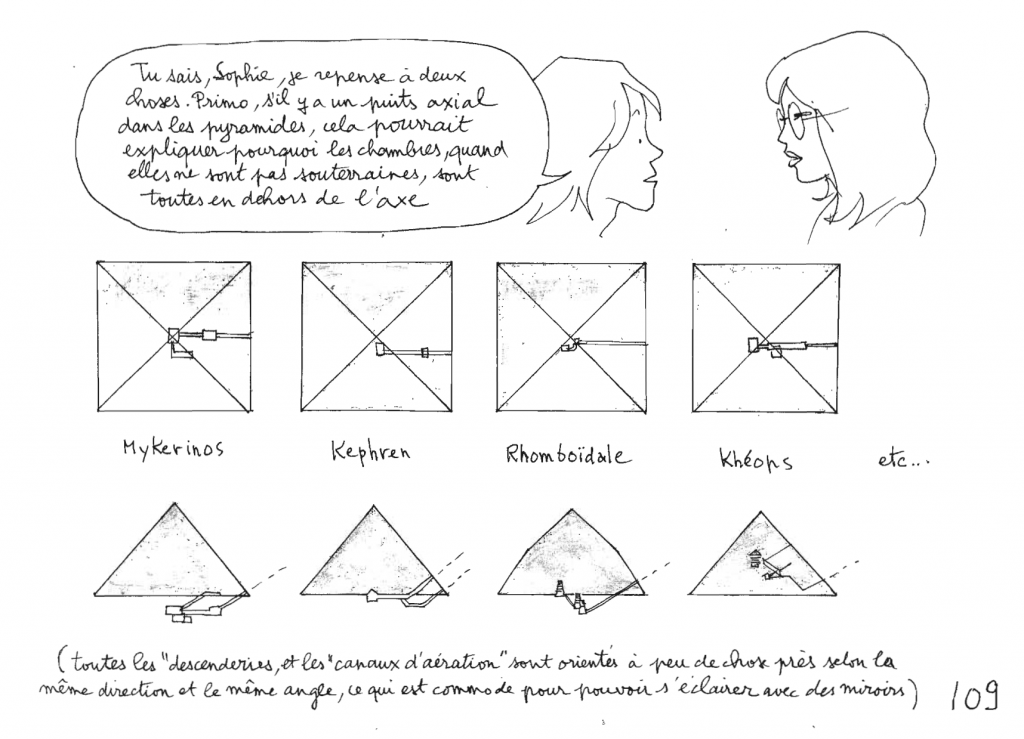
Dans le préface de ce livre, Burattini décrit sa visite de la grande pyramide de Gizeh en 1639 avec John Greaves. Ce dernier était un astronome anglais spécialisé en métrologie ancienne. Graves a publié en 1646 un livre avec ses mesures de la grandes pyramide de Gizeh.
Le physicien Isaac Newton s'est intéressé aux mesures de Graves (et Burattini) dans le but de trouver la valeur de la coudée royale égyptienne. Il était convaincu que les anciens égyptiens avaient déterminé la dimension de la Terre et que la valeur de la coudée pourrait l'aider à déterminer avec précision la circonférence de la Terre.
Tout ceci dans le but d'affiner sa théorie de la gravitation. Malheureusement Newton n'a pas trouvé dans les mesures de Graves ce qu'il cherchait et il a du attendre la mesure d'un degré de méridien effectuée en 1669 par Jean Picard.
Entre 1735 et 1744 Charles Marie de La Condamine mène une expédition à Quito en équateur pour mesurer les 3 premiers degrés de méridien depuis l'équateur et ainsi déterminer la figure de la Terre. Est-elle aplatie aux pôles comme le prétend Newton, ou à l'équateur comme le prétends Descartes ?
Ainsi deux équipes sont envoyées mesurer des méridiens près des pôles et près de l'équateur. Finalement c'est Newton qui avait raison.
Pendant cette expédition, Charles Marie de la Condamine imagine lui aussi l'utilisation d'un étalon universel basé sur un pendule qui bat la seconde. Mais à l'équateur pas n'importe où, à l'équateur.
Cette définition ne sera pas retenue bien que l'idée du pendule sera soutenue par Talleyrand. (bon, lui il préférait la latitude de 45°) (De plus aux USA, Thomas Jefferson était aussi partisan du pendule)
Néanmoins, la mesure du degré de méridien par la Condamine sera utilisée pour déterminer le mètre, vu que l'idée d'extrapoler la mesure de la portion de méridien de Méchain et Delambre pour en trouver le 1/4 du méridien est remis en cause par la découverte que la figure de la Terre, n'est pas une élipsoïde de révolution, mais que chaque méridien a sa mesure propre.
Puis il y a l'abbé Lacaille qui a mesuré entre 1750 et 1754 un bout de méridien en afrique du sud, puis la géodésie de l'ile de france. Il est mandaté après la mort du roi en 1791 pour déterminé le "mètre provisoire" . Ce sera fait en 1793 (plus long de 0,095 mm que le mètre réel) et exprimé en toise du pérou. Il est remplacé par le vrai mètre en 1799. Ironie du sort, le "mètre vrai" est plus faux que le provisoire !!
Ce mètre vrai de Delambre et Méchain trop court de 0,23 mm !!!
Mais cette erreur de mesure a été retranscrite et continue a être officielle de nos jours.
Il est intéressant de voir que dans son décret, le 8 mai 1790, l'assemblée avait choisi une définition du mètre basée sur le pendule qui bat la seconde. A 45° de latitude ou tout autre qui pourrait être préférée. Il est aussi fait mention qu'on "supplie" le roi de demander aux anglais de collaborer sur ce sujet. (un projet similaire était en cours !)
Le 26 mars 1791, la commission décide que le pendule dépend de la seconde et n'est pas une bonne mesure. Le 1/4 de l'équateur non plus, car c'est loin et ne correspond qu'à une partie des humains. Donc c'est le 1/4 du méridien qui est choisi.
Il est proposé d'aller mesurer le morceau de méridien entre Dunkerque et Barcelone soit 9.5° et d'en extrapoler la mesure du 1/4 du méridien en supposant que la Terre est une ellipse de révolution. Ce qui finalement c'est avéré faux....
L'idée que le pied est basé sur la taille du pied du roi c'est mal comprendre cet ancien système
C'est bien mal comprendre le système de la coudée, des pieds que de raconter cette fable qui explique que le pied de l'unité de mesure est le pied du roi !
Si on connait un peu la géométrie sacrée et le savoir des bâtisseurs de cathédrales, on découvre que ce système de paume, palme, empan, pied, coudée, n'est pas fait au hasard et que la dimension n'est pas faite en référence à des parties du corps, même si il y a une similitude d'une part ménémotechnique et d'une autre part de la structure du corps.
La système de "quine des bâtisseurs" (aussi appelé parfois "pige des bâtisseurs" ) est construit sur la base d'une division en proportion dorée. (au lieu de la division décimale)
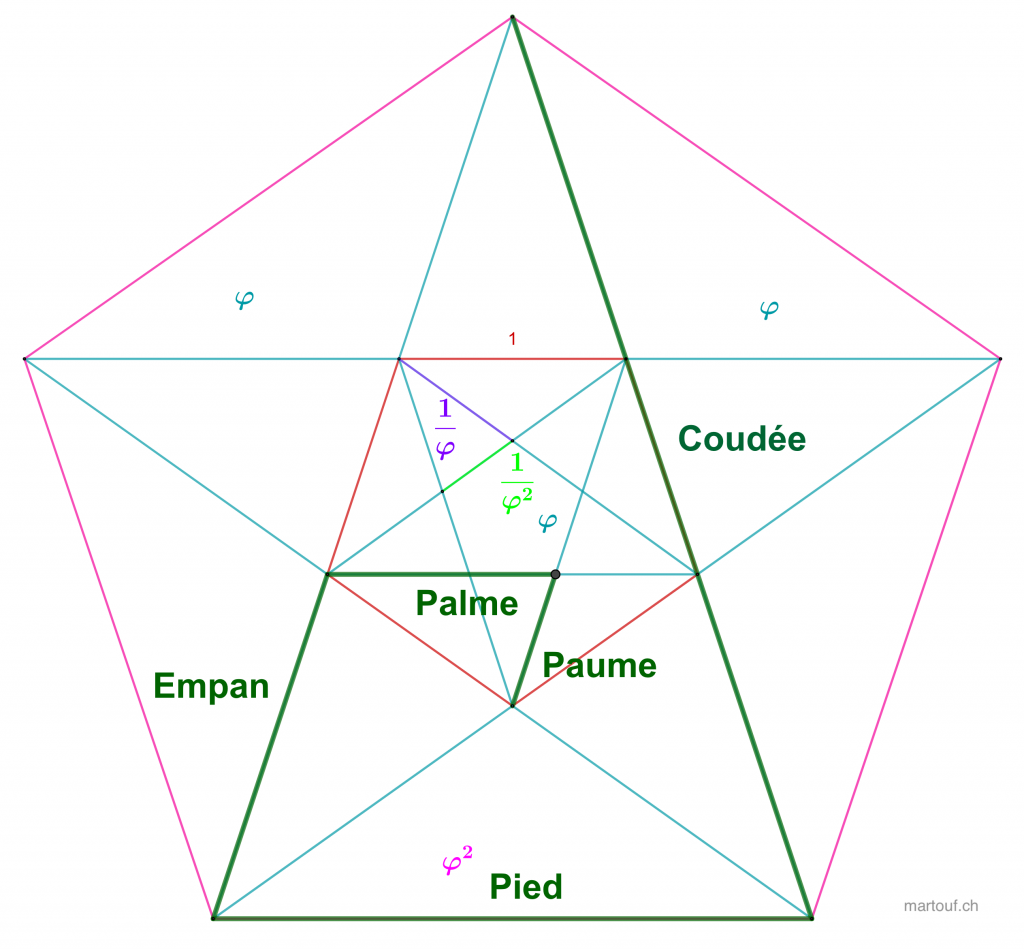
Il se trouve que ce système de quine est aussi en lien avec le mètre !!
En effet, l'empan vaut 1/5 de mètre !
Mais la coudées royale est aussi en bonne approximation 1/6 de la circonférence d'un cercle de 1 mètre de diamètre.
Par quel mystère est-ce possible ? Le hasard ? Une connaissance transmise dans les confrérie de bâtisseurs ? Une mesure retrouvée dans la pyramide par ses visiteurs et proposée comme définition de la nouvelle mesure universelle ?
Je ne sais pas. Mais je cherche.
Comme point de départ, je cherche si le mètre se trouve dans des endroits significatifs sur des monuments existant. De là on pourra voir si il y a une cohérence, une idée de technique simple qui pourrait expliquer ce mystère. (peut être le pendule ?)
Nous allons faire ici une liste la plus exhaustive possibles d'occurrences de l'utilisation du mètre dans un passé plus ancien que 1800.
Liste de monuments et objets anciens qui indiquent le mètre
Le disque de Nebra
Le disque de Nebra fait 1m de circonférence.

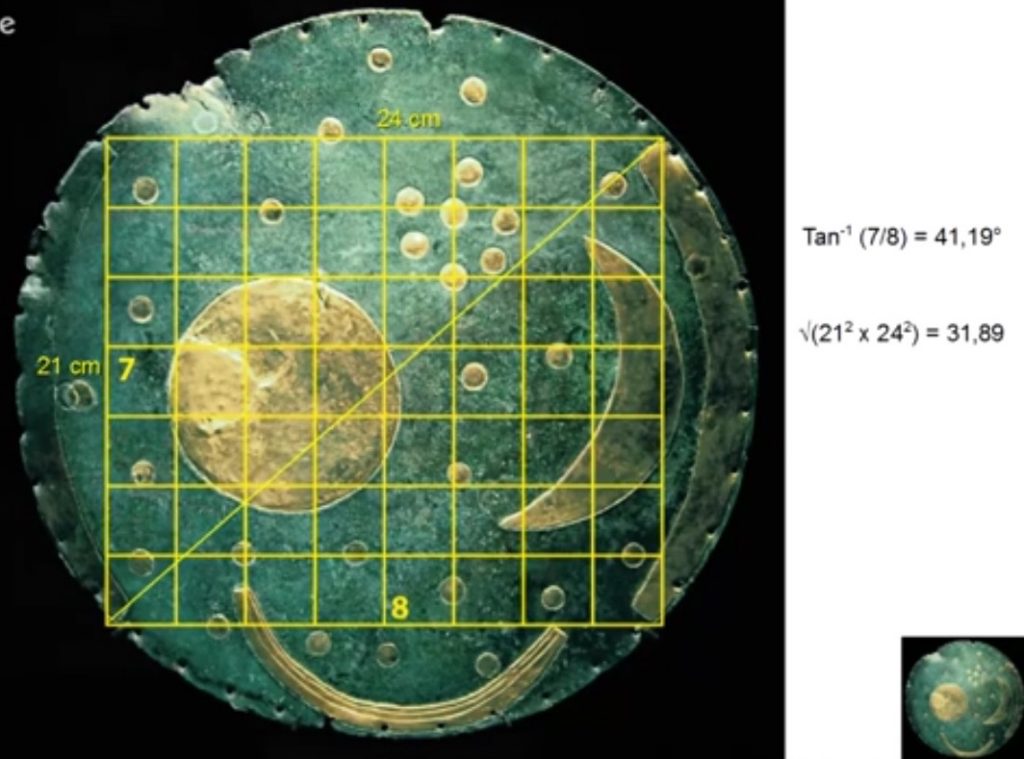
En plus du mètre, on observe des mesures en centimètres. Le cercle du soleil fait 10cm de diamètre, celui de la lune fait 13cm, de diamètre, tout comme la distance entre les pointes de la "barque solaire" ou "ciel de nout", (tout dépend de l'orientation du disque)
Le rectangle solsticial sur l'image ci-dessus fait 24cm * 21cm.
Il y a vraiment beaucoup d'unité de mesure en cm.
Mais la distance entre les trous, très proche de 2,54cm... ce qui correspond au pouce anglais !
Pour en savoir plus sur cet ordinateur astronomique qu'est le disque de Nebra, voici mon article....
Stonehenge
Le cercle de pierre a une circonférence de 100,02m.


Voici les mesures de Flinders Petrie, à convertir en mètre pour que ce soit clair..
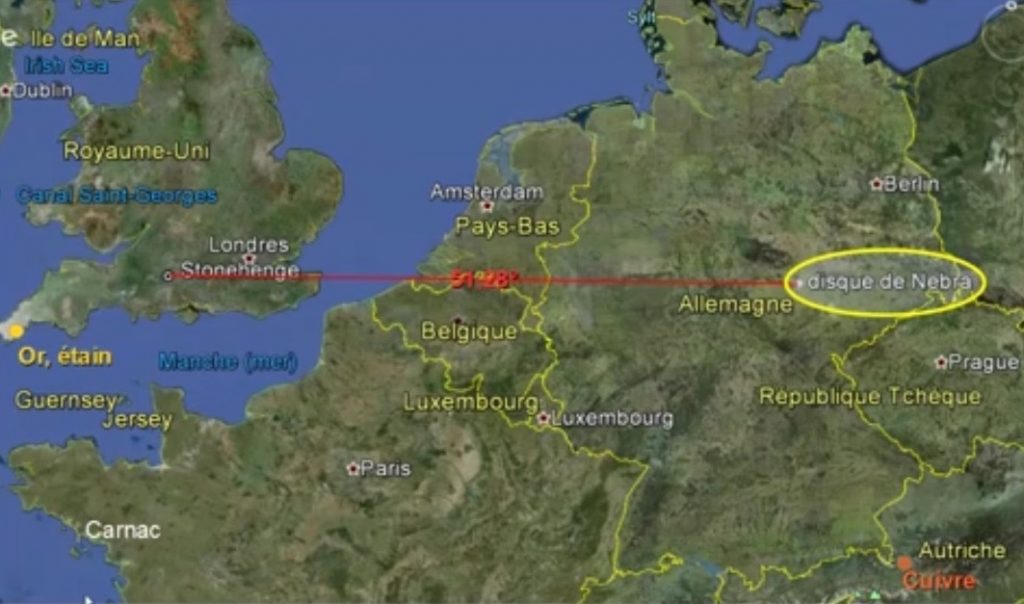
Il se trouve que Stonehenge (51° 10′ 44″ N ou 51.17888) est à une latitude similaire de celle de Nebra. (51° 17′ 02″ N)
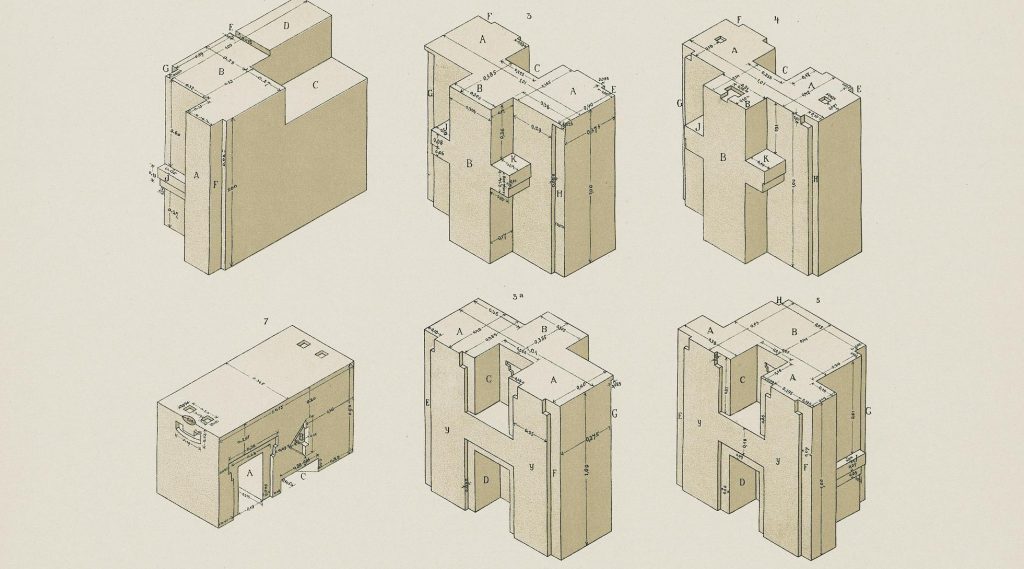
Les blocs en H de Puma Punku
Les blocs en H de Puma Punku font 1m de Haut.
Voici les images de la mesure tirée du film BAM.


Voici également les mesures complètes faites par A. Stübel et publié en 1892.
L'église de Saint-Nectaire contient une niche de 1 mètre et une pierre de 1 coudée l'un à côté de l'autre
Dans l'église de Saint-Nectaire en Auvergne, il y a une niche qui fait 1 mètre de large et ceci juste au dessus d'une pierre qui fait 1 coudée de large. (pour le détail sur le lien entre la coudée et le mètre est voir en bas de l'article)
Ces pierres sont montrées dans le film BAM.


La diagonale des pierres angulaires de la Cathédrale de Fribourg fait 1 mètre
Dans le dallage de la Cathédrale de Fribourg (suisse), il y a les pierres angulaires qui ont servies de référence pendant le construction. La construction a débutée en 1283.

Ce sont en fait deux pierres allongées en granite. Le granite est très solide et ne se dilate pas. Cette pierre a du servir comme étalon de mesure pour construire la cathédrale. En fin de chantier elle a été intégrée au dallage.

Comme on l'a vu ci-dessus, en géométrie sacrée c'est souvent la dimension des diagonales qui compte, et là on ne va pas être déçu....
Mais au passage, sache déjà que le petit côté de ce rectangle est formé par deux fois 1 pied romain. (29,635 cm)
(Le pied romain est toujours très utilisé de nos jours... c'est la hauteur d'une page A4 !!! soit 29,7cm)
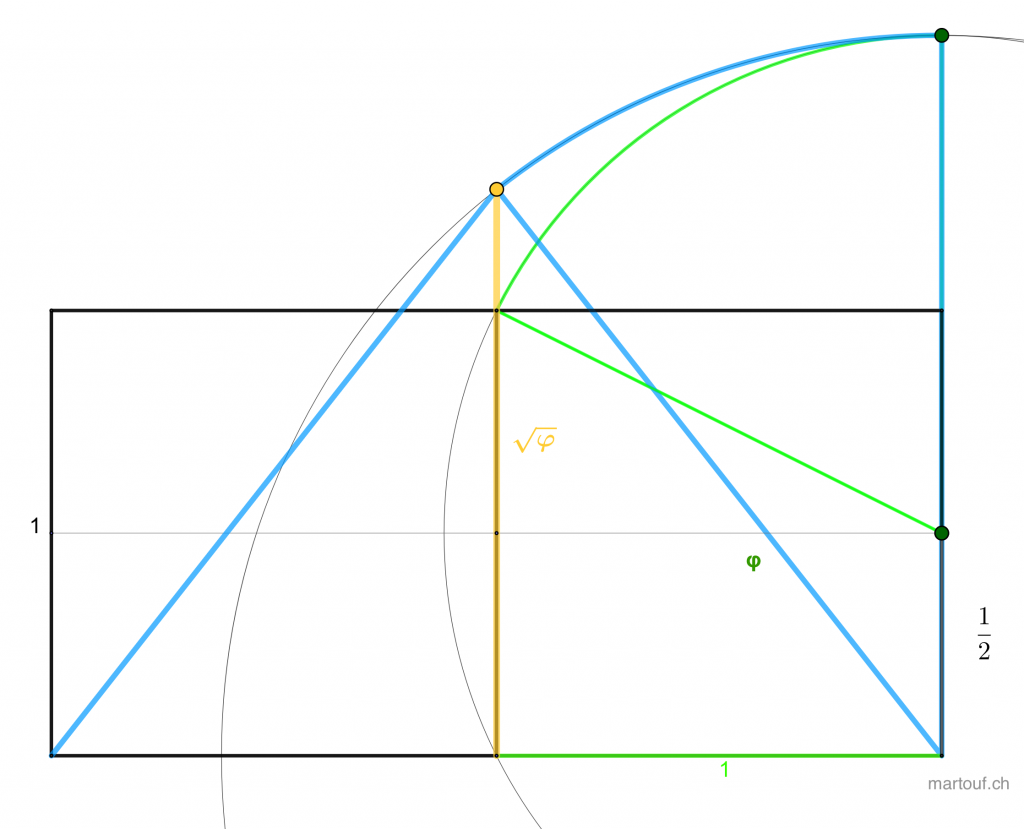
La longueur des pierres fait 80,56cm. Ce qui correspond à √φ * la coudée sacrée de 63.3 cm. (une coudée qui en lien avec le rayon de la terre )

La diagonale de la pierre angulaire de la cathédrale de Fribourg vaut 1 mètre !!!
... et oui, le mètre est bien plus ancien qu'on le dit officiellement.
Diverses cathédrales en Europe
A la p.249 du livre "géométrie sacrée" de Stéphane Cardinaux. Il est dit que l'on trouve dans plusieurs cathédrales en europe des pierres angulaires marquant plusieurs unité de mesures connues, dont le mètre.
Il s'agit des pierres angulaires de l'Église Notre-Dame de Saint-Saturnin, de la Cathédrale Notre-Dame de Laon, de la Basilique Notre-Dame d'Orcival, et de la Cathédrale Saint-Nicolas de Fribourg.
Je n'ai visité personnellement que cette dernière, et effectivement comme montré ci-dessus, j'y ai vu sous le porche d'entrée les pierres angulaires, dont la diagonale mesure 1m !
Donc si qq'un est allé voir les autres cathédrales, je suis preneur d'info. Merci
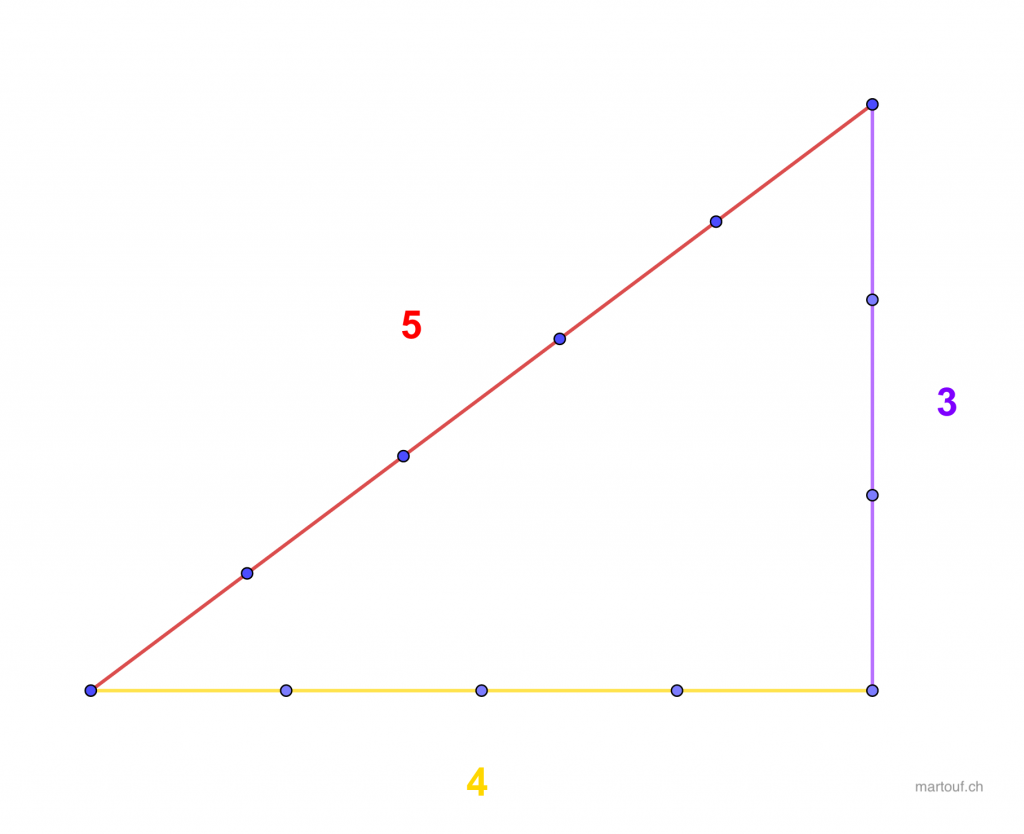
Voici à quoi ressemble les pierres angulaire de la cathédrale de Laon. Ces pierres sont enchassées dans le dallages du sol, mais pas dans la même orientation. Il semble y avoir aussi un lien par là avec une orientation. L'axe est-ouest est perpendiculaire à la l'hypothénuse du triangle 3-4-5.
Liste de portes de monuments avec une taille liée au mètre
Quentin Leplat a fait une étude en mesurant les portes de nombreuses vieilles église et château.
Il y a de nombreuses portes de monuments du XI au XVIII ème siècle qui ont une taille liée au mètre.
Quelques exemples issus de cette étude:
- La largeur de la porte gauche de la façade de la cathédrale Notre-Dame de Paris mesure exactement 2,000 m.
- La largeur des portes du donjon du Château de Chambord mesure 1,000 m et 90,0 cm
- Les deux gravures fichées dans les murs de l’Abbatiale de St- Nectaire du 11ème siècle mesurent 1,00m et 52,4 cm
- La grande pierre fichée dans le mur de l’abbatiale de Conques mesure 1,00 m.- EGLISE DE ST DIERY , la porte mesure 100 cm ± 0,1.

Le Coricancha basé sur le mètre
La salle mesure 10m de long à ± 0.01 et largeur des murs de 1m ± 0,005
Les niches avec un schéma directeur basé sur un double carré de 44.72 cm de côté, donc la diagonale du double carré vaut 1 mètre


Quentin Leplat nous en parle dans cette vidéo:
Voici toute les références de Quentin Leplat à propos du Coricancha...
La porte du soleil a Tiahuanaco fait 3 mètres de haut et 4 mètres de large
La porte du soleil à Tiahuanaco a des proportions très particulières en géométrie sacrée, avec le nombre d'or partout, mais il se trouve aussi que cette porte a une hauteur de 3 mètres et une largeur de 4 mètres.
Ce qui forme même un triangle 3-4-5 le premier des triangles rectangles, ceci exprimé en mètre !

L'Ahu de Tongariki sur l'ile de Pâques fait 100m de long
L'Ahu de Tongariki est une plateforme sur l'ile de Pâques qui soutient des Moaï, ces grandes statues. Tout le monde regarde les statues, mais les dimension du socle sont impressionnantes: 100m de long.
Et la rangée devant fait 220m de long. Ça marche aussi en mètre.

Grottes de Barabar
Les grottes de Barabar en Inde sont taillées dans le granite, elles ont au moins 2300 ans.
Des scan 3D au laser des grottes de Barabar ont été réalisés ces dernières années et montrent une grande précision milimétrique du poli de ces grottes. Mais on y remarque aussi les dimensions qui semblent être basées sur le mètre.
Par exemple, voici la grotte de Sudama, qui est composée de 2 pièces:
une salle rectangulaire de 9.98 m de long sur 5,94 mètre de large. (On est pas loin du 10 x 6 mètre....) et une pièce en forme de dôme de 6m de diamètre.
Mais le reste est encore plus impressionnant.

Le scan 3D très précis nous montre pour la première pièce une hauteur de 4.0905 mètre.
Puis pour la seconde pièce, le centre du dôme est situé à 1,0113 mètre du sol. De là, c'est un rayon de 3,0513 mètre qui forme le dôme de la grotte. Donc au total, on a une hauteur maximale de 4,0799 mètre.
Un film est prévu sur les grottes de Barabar pour mars 2021:
BAM : COMPRENDRE BARABAR
Voici déjà un aperçu pour donner envie en 5 minutes.
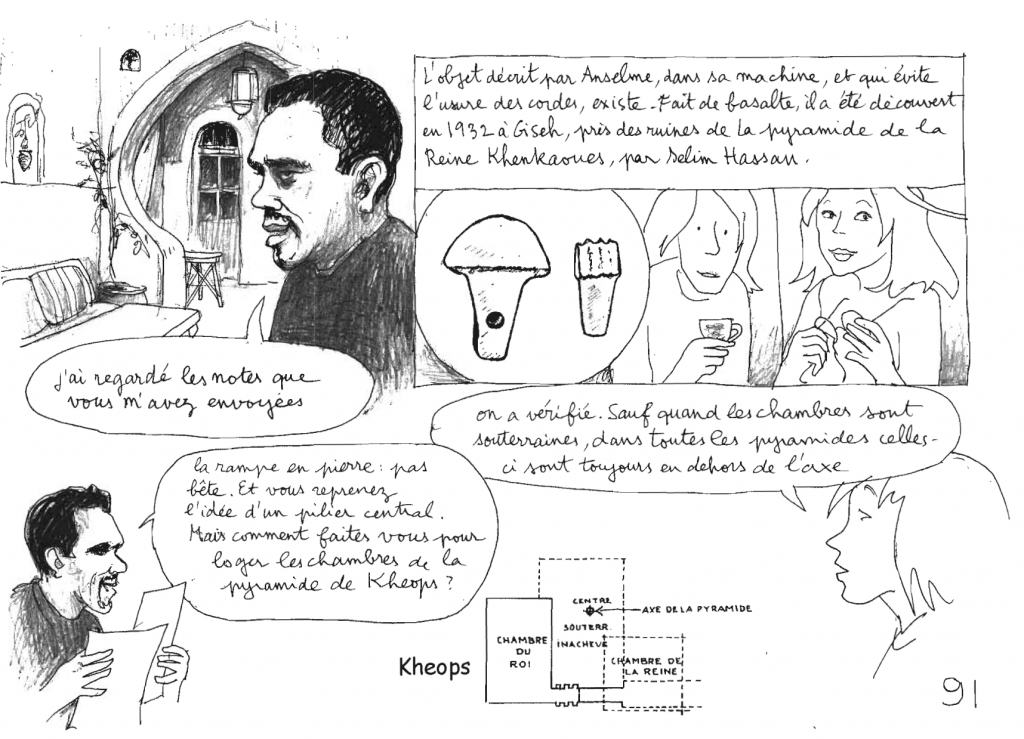
Le mètre est présent dans la chambre de Khéops
La fameuse chambre haute de la grande pyramide de Gizeh a des dimensions totalement en accord avec la géométrie sacrée, donc en lien avec le mètre, voir le détail ci-dessous....
Mais plus directement il y a aussi une mesure en mètre d'un endroit très particulier dans cette chambre.
C'est la distance entre le sol et le centre du conduit du mur Nord de la chambre du roi. Le centre de ce conduit étant à exactement 5 coudées royales égyptiennes de la droite du mur, on a la un indice qui nous montre que ce centre du conduit n'est pas placé au hasard.
Voici le plan de ce mur refait par l'apprenti sage, sur la base des mesures de Gilles Dormion.
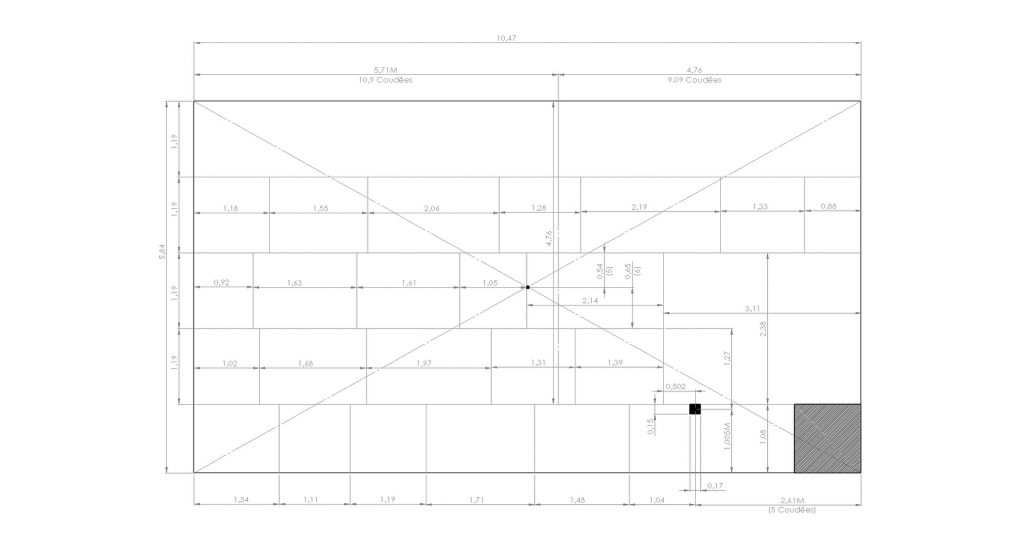
Voici l'explication en vidéo.
Distance Olympie - Mycène = 100 km
Olympie est le centre du monde grec. Et on dirait bien que les villes ont été placées sur un rayon de 100 km.
En tout cas c'est la position de Mycène. (et d'autres à vérifier)

Le planétarium de Gizeh
J'ai déjà fait tout un article sur le sujet du planétarium de Gizeh, tellement c'est incroyable.
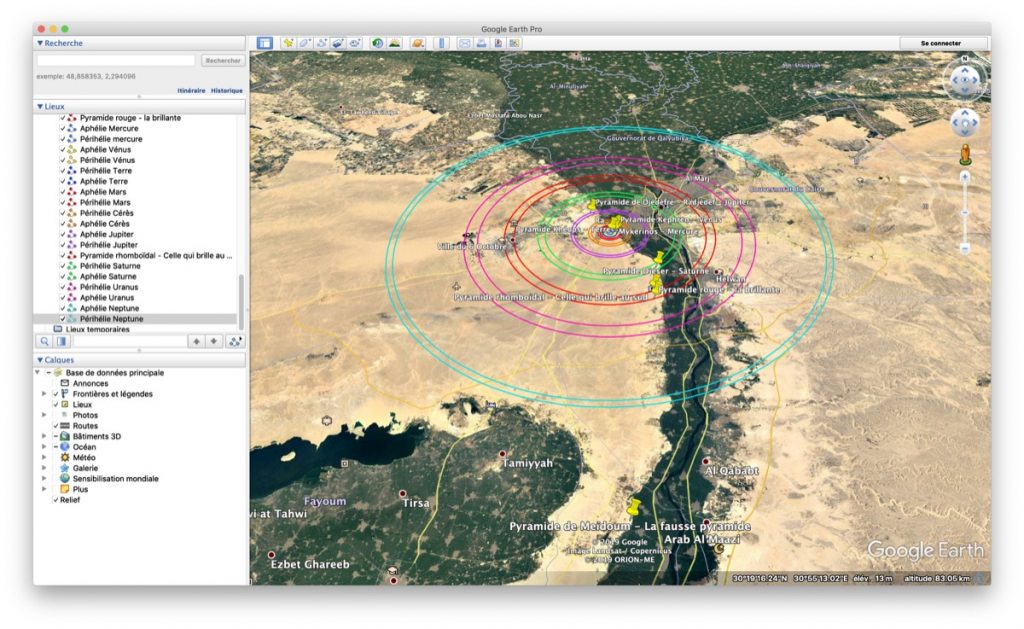
Mais il semble bien que les pyramides du plateau de Gizeh représentent les planètes du système solaire !
- les pyramides symbolisent les planètes du système solaire
- les pyramides sont placées sur les orbites moyenne des planètes à une échelle de 1:100 millionième
- les pyramides ont des tailles apparentes vues depuis le lieu symbolisant le soleil qui sont en relation avec leur magnitude apparente.
L'échelle est donc une échelle en mètre !!
J'ai joué avec Google Earth et ça semble marcher en bonne partie. Si tu veux vérifier par toi-même, voici mon fichier kml que tu peux reprendre ici.
Unité de mesures anciennes liées au mètre
Il existe plusieurs anciennes mesures liées directement ou indirectement au mètre.
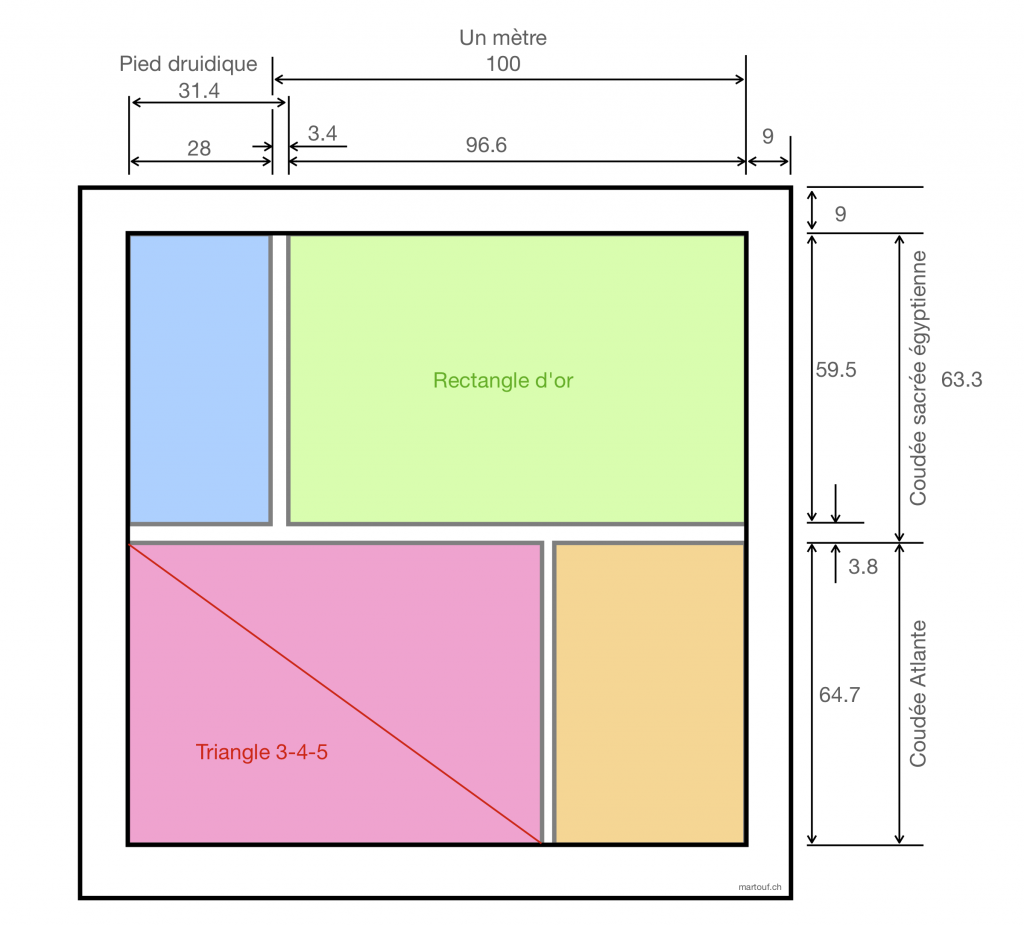
Le pied Drusien
Le pied Drusien mesure 33.3396 cm. Soit ~1/3 de mètre.
La coudée royale égyptienne
La coudées royale égyptienne est la même que la coudée des bâtisseurs de cathédrales.

Selon moi, il y a deux définition de la coudée royale égyptienne, la version masculine basée sur la droite et la version féminine basée sur le cercle.
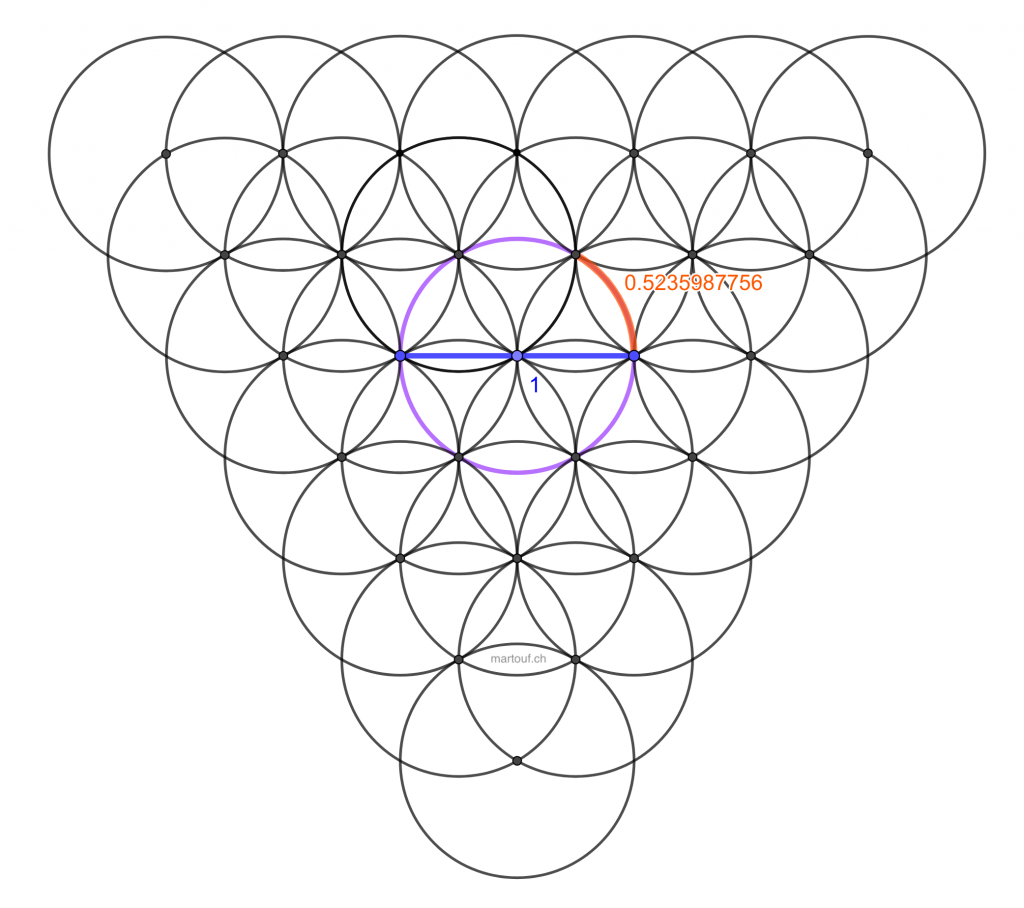

L'empan correspond à 1/5 de mètre
Le système de la coudée s'inscrit dans le système de la quine des bâtisseurs avec des subdivisions en lien d'une proportion dorée.
L'empan, une mesure qui est liée à la distance entre le pouce et l'auriculaire vaut 1/5 de mètre: 20 cm.


Expressions qui suggèrent la connaissance du mètre
Il y a des longueurs qui ne sont pas directement en mètre, mais qui laissent penser que le mètre était connu.
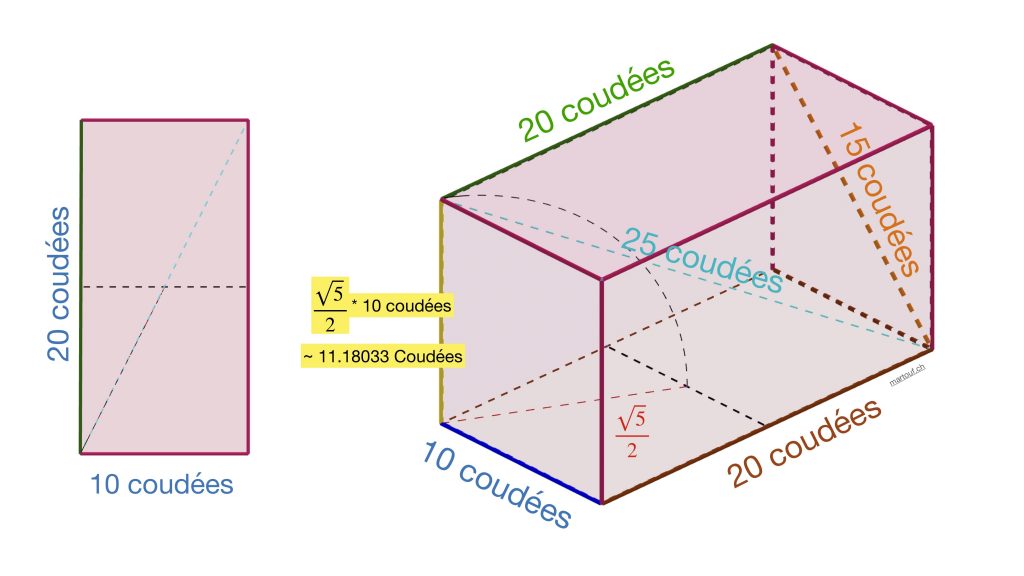
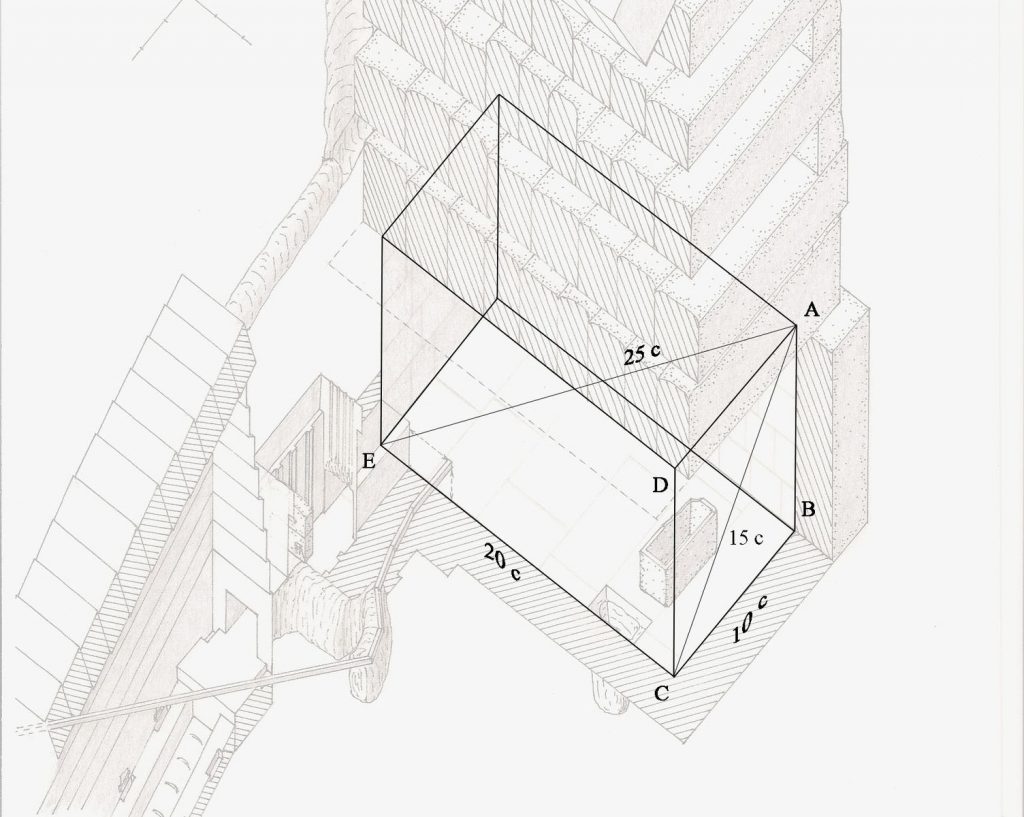
C'est par exemple le cas de la géométrie de la chambre haute (dite du roi) de la grande pyramide de Gizeh (dite de Khéops).
Le sol de la chambre est un double carré, forme qui ouvre sur pleins de notions en géométrie sacrée.
Mais au delà des proportions, il y a la taille de la chambre. On peut la faire à n'importe quelle taille, en tout petit microscopique ou géant... mais il n'y a qu'une seule taille qui fait ressortir l'expression de π et du nombre d'or si on mesure en mètre et c'est cette taille là qui justement a été choisie et pas l'infinité des autres !!
Certains dirons que c'est du hasard... mais faut quand même souligner que la probabilité que ça arrive reste très très faible.
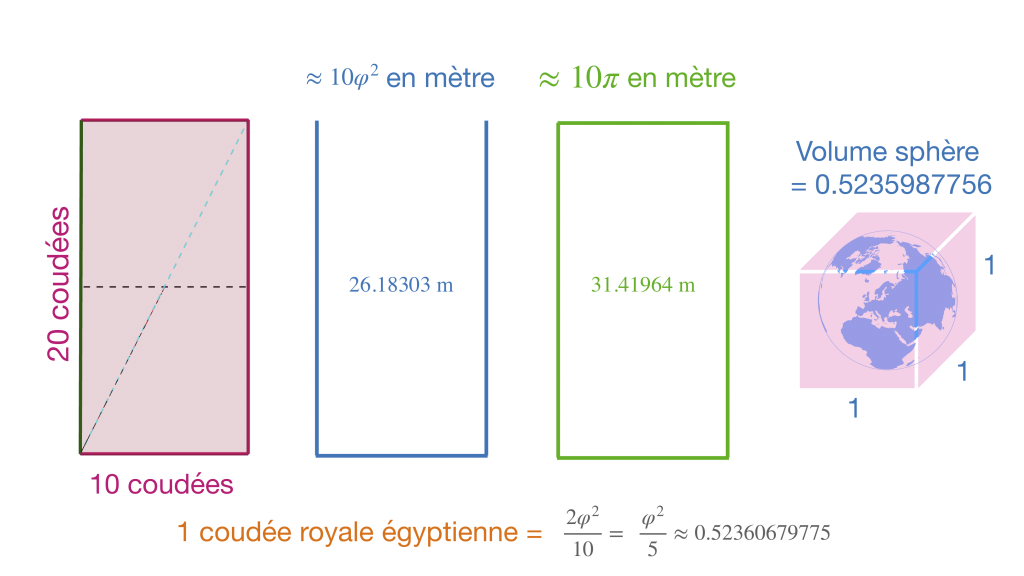
Ainsi le périmètre du sol de la chambre vaut 31.42964 m ce qui est une bonne approximation de 10 fois π.
Le périmètre moins un petit côté, mesure 26,18303 mètre et ce qui équivaut à 10 fois phi, le nombre d'or.
Il y a évidemment une petite différence au niveau mathématique, mais au niveau de la précision de construction d'un bâtiment, pas certain qu'on puisse faire plus précis ! On parle d'une précision milimétrique !
A compléter...
Je sais qu'il y a encore beaucoup de d'autres exemples, notamment indirect par calculs et quand on mesure des alignements un peu partout. Donc cette liste est à compléter.
Tout n'est pas encore claire. Mais garde l'esprit ouvert...
... et si tu as des exemples, n'hésite pas à les ajouter en commentaire.
Afin de vérifier l'étude de Quentin Leplat sur les portes, voici une nouvelle étude qui est lancées pour aller mesurer des anciennes portes. En parler, c'est bien.. agir c'est mieux.... à bientôt.