Qu'est-ce que l'univers ?
Et bien de plus en plus j'ai un faisceau d'indices qui tendent à m'indiquer que nous vivons dans un jeu vidéo !
... et là je crois que j'ai trouvé la preuve ! .... oui oui... Je parle bien de preuve, car c'est une sorte de signature que j'ai trouvée.
C'est complètement fou, mais là j'ai besoin d'un peu de temps pour t'expliquer tout ça.
Il me faut poser quelques bases pour que je sois bien compris.

Version vidéo de cet article
L'hypothèse de la simulation
Il y a un courant de pensée grandissant qui pense que nous vivons dans une simulation informatique.
Le philosophe Nick Bostrom a même déclaré il y a une vingtaine d'année que nous avons une probabilité de 1/3 de vivre dans une simulation.
Il a même ajouté que les auteurs de cette simulation sont probablement nos descendants qui nous simulent pour voir comment on se comporte.
L'état du débat sur l'hypothèse de la simulation peut se suivre sur le site: simulation-argument.com
Un vieux débat philosophique
Ce débat n'est pas nouveau du tout. Il a même quelques millénaires. L'idée d'un monde virtuel est déjà proposée dans le mythe de la Caverne de Platon.
Ou encore en Chine chez l'un des fondateurs du taoisme, Tchouang Tseu et son rêve du papillon.

Un thème récurent dans le cinéma
Le monde virtuel est le thème de films comme eXistenZ, Passé virtuel ou Matrix. Chose étonnante c'est que ces 3 films sont sorti la même année en 1999 !

Les films ci-dessus ont une approche liée à la science fiction. C'est un moyen technique qui crée un univers virtuel.
Il y a des ambiances cyberPunk comme dans Matrix, avec plein de bidouillages avec du matos qui a l'air de sortir de la déchèterie.
Il y a mêmes des couplages de machine improbable qui font tourner des téléphones à cadrant déjà obsolète depuis longtemps en 1999 ! ... mais tout à fait dans l'ambiance du film Passé virtuel qui parle d'un univers placé dans les années 1930 !

On a aussi des ambiances plutôt biologiques comme dans le film eXistenz.. voir le film complet ici...
Dans eXistenz la technique connexion est biologique. Les utilisateurs jouent avec des pods et les connectent sur la moelle épinière.

Une décennie plus tard, le thème du monde virtuel revient au cinéma.
En 2009, on a le film Avatar qui nous montre une technique pour s'incarner dans un être biologique: un avatar. Le nom vient directement concept indien d'Avatar qui représente l'incarnation d'un dieu. Comme Vishnou qui s'incarne en Krisna. On reconnais les avatars de Vishnou car ils sont souvent bleu !
Le Bouddha (aussi avatar de Vishnu), est un titre qui vient su sanskrit et signifie "éveillé".
L'idée est ici de s'endormir dans une réalité inférieure imbriquée, ou de remonter dans une réalité supérieure plus réelle et donc de s'éveiller...

Ce concept de sommeil, s'éveiller ou s'endormir est le sujet du film Inception sorti en 2010.
Ici la technique change encore, on est dans le principe du rêve. La technique se réduit et devient très discrète, il s'agit d'administrer un sédatif pour faire dormir les personnes.
Le film joue beaucoup sur le principe d'imbrication et de distorsion temporelle qui en résulte.

Une décennie plus tard, facebook annonce que l'entreprise change de nom pour devenir Meta. Ceci afin de s'orienter vers la création d'un métavers.

Facebook semble vouloir réaliser concrètement le monde de l'Oasis que l'on voit dans le film de Spielberg Ready Player One sorti en 2018.

Peu importe la technique le thème de l'univers virtuel est récurrent
J'aime à dire que:
Le propre de l'Homme c'est de (se) raconter des histoires.
En effet, depuis la nuit des temps, l'Humain se crée des univers virtuels dans des histoires. Depuis les contes au bord du feu, au métavers, en passant par le théâtre, la chanson, les livres, les films et les jeux vidéos.
Il y a un profond intérêt pour l'Humain de se créer un univers virtuel dont il est le démiurge ou de vouloir sortir de la réalité dont il est prisonnier, en s'éveillant.
J'ai déjà écrit un article ce propos, donc pour aller plus loin c'est par ici....
Maintenant il est temps d'avancer dans la "LA" preuve que nous sommes dans un univers virtuel, un jeu vidéo..
La physique quantique va dans le sens d'un univers langage
L'univers n'est pas une boite dans laquelle il y a des objets. Ce n'est pas un espace-temps. C'est surtout une grosse base de données relationnelles. L'univers est un langage. Il y a de requêtes qui sont effectuées pour afficher sur un "écran" la réalité du moment.
Voici donc en bref ce que j'ai décrit dans une autres article...
La physique quantique a maintenant une centaine d'année, mais n'est toujours pas bien comprise. Mais avec la métaphore de l'informatique tout de vient compréhensible.
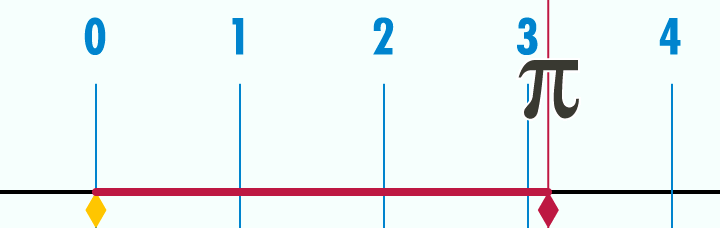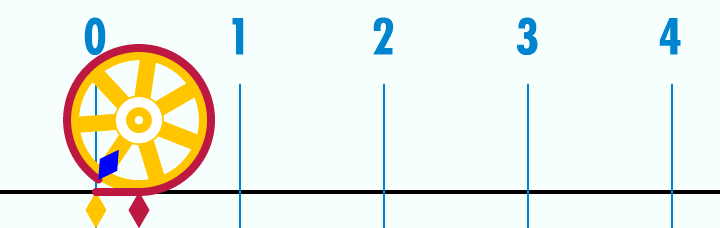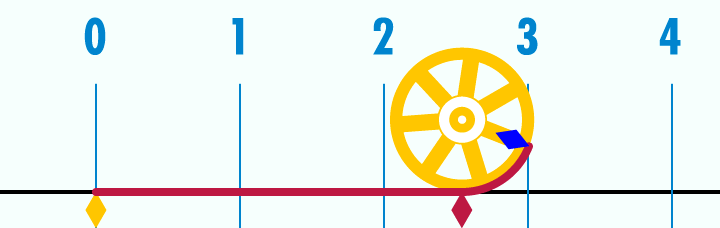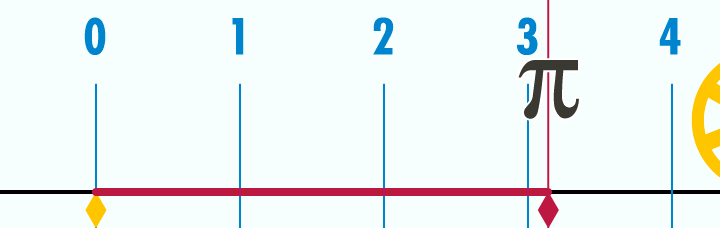
- la longueur de Planck c'est un pixel.
- l'observateur est nécessaire pour manifester une réalité, même si le potentiel en base de donnée de toutes les autres réalité existe.
- C'est comme pour ce blog. Ils y a des centaines d'articles en base de donnée, mais ton navigateur web n'en affiche qu'une poignée, juste ce qu'il faut pour ta réalité du moment.
Donc notre univers n'est pas totalement figé et objectif. C'est une co-création manifestée quand on l'observe. Ceci autant dans le futur que dans le passé ! C'est une oeuvre d'art qui porte du sens.
La synchronicité est le premier pas pour comprendre le fonctionnement d'une conversation avec l'univers.
Donc voici notre quête de sens.
L'univers est un jeu vidéo !
On devrait donc trouver un concepteur, le grand architecte, mais surtout sa signature.
... et là je pense l'avoir trouvée !

Easter egg
A une époque les développeurs de jeu vidéo n'étaient pas crédité. En 1978 chez Atari, Warren Robinett, avait tout de même envie de signer son jeu: Adventure. Il a donc trouvé un moyen original de signer son oeuvre.
Adventure est un jeu de labyrinthe. Il a donc créé une pièce spéciale dans laquelle si on amène un objet en particulier, le nom de Warren Robinett apparait !
(les graphismes actuels nous font oublier qu'il fallait une dose d'imagination à l'époque pour jouer aux jeux vidéo, oui, c'est pixelisé !!)
Voici donc comment est né le premier easter egg 🥚. C'est une signature.
Cette histoire est relatée dans le film Ready Player One mentionné ci-dessus. C'est même le coeur de l'intrigue.
La quête du héro est de trouver l'easter egg, qui a été caché par le concepteur de l'Oasis, la réalité virtuelle la plus utilisée.
Un Easter egg est littéralement un Oeuf de Pâques. Donc le film Ready Player One est une chasse aux oeufs !
En français le terme easter egg, désigne surtout un clin d'oeil du concepteur d'un programme informatique ou d'un jeu vidéo. Tout comme l'a fait Warren Robinett, de nombreux développeurs cachent des easter egg, ce qui permet de prouver qu'ils en sont les concepteurs.
Voici quelques exemples actuels d'easter egg
Si tu as la chance d'utiliser Firefox comme navigateur web, alors tu peux directement expérimenter des easter egg.
Tape dans la barre d'adresse: about:mozilla
:... et tu verras apparaitre un extrait du livre de Mozilla !
Toujours dans firefox, tu peux taper:
about:robots
... et suis les instructions du robot... ou pas !
Bon, si t'as pas la chance d'utiliser Firefox, voici un autre easter egg.. tu vas regarde la source html de la page d'accueil d'Amazon... et tu verras un canard qui se prend pour un chat !
Bon... et bien voilà, je crois que le concept d'easter egg est maintenant connu.
Alors partons à la chasse à l'easter egg dans notre monde !
Google..... Easter...
Bon, alors je me dis que si l'univers est porteur de sens, alors il suffit de lui demander où se trouver l'easter egg et c'est gagné !
Comment je lui demande ?
Si je cherche un lieu, je lance google maps... et je tape.... Easter...
Boom.... google complète.. Easter Island... L'ile de Pâques, Rapa Nui.....
Quoi de mieux comme Easter egg, qu'une ile nommée Easter !?
Je le rappelle, l'univers fonctionne avec des liens de sens, pas autre chose !
Easter Island - Ile de Pâques - Rapa Nui - Le nombril du monde
Bon.. et bien l'ile de Pâques, c'est loin ! ... Loin de tout !
C'est perdu au milieu de l'océan pacifique.
C'est la terre habitée la plus éloignée d'autres habitants ~3600 km du Chili.
C'est une roche volcanique 🌋, une roche de feu 🔥 perdue au milieu d'un désert d'eau. 💧

L'ile de Pâques s'appelle ainsi à cause d'un navigateur Hollandais qui est passé par là en 1722 le jour de Pâques.
Pâques se dit Easter en anglais, mais le nom vient de la fête celtes de Ostara (ou Eostre). La fête de l'équinoxe de printemps. C'est le renouveau de la nature, la fertilité – d'où la symbolique du lapin – mais aussi des oeufs de Pâques.
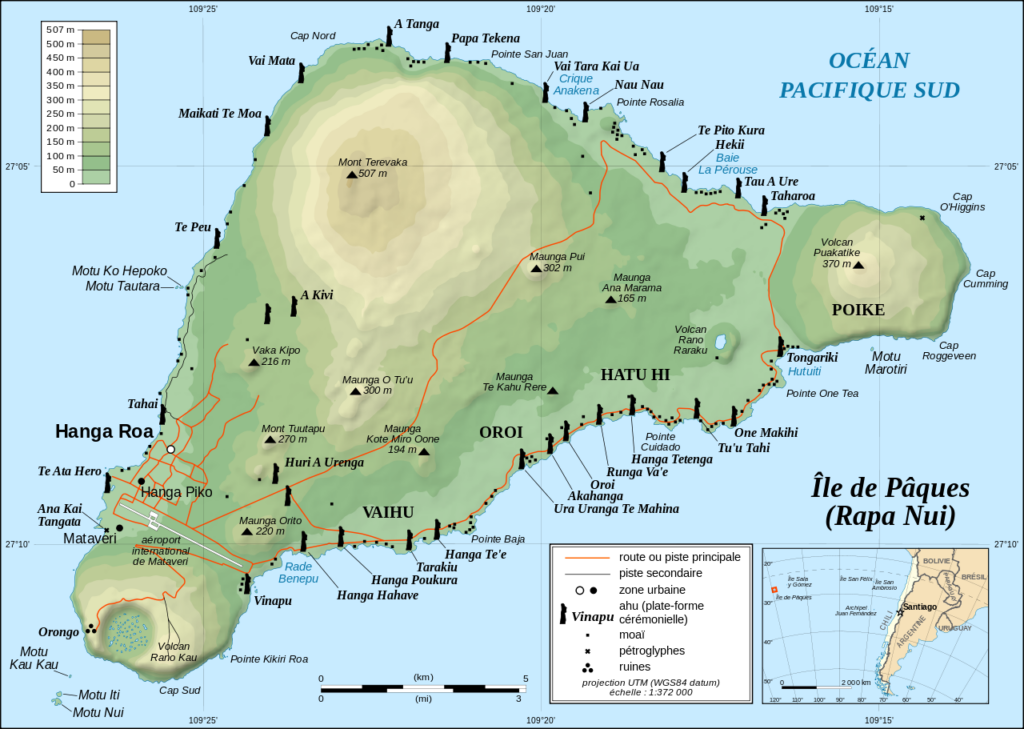
Mais en fait selon les locaux, le nom de l'ile c'est Rapa Nui (la grande rapa).
... et en fait c'est encore plus compliqué, car Rapa Nui est un nom donné par des visiteurs Thaitiens. Un autre nom de l'ile plus ancien est MATA-KITE-RANI. Ce qui signifie "des yeux regardent le ciel".
Ceci probablement en référence à ses statues monumentales, les moaï.

.... mais en fait c'est encore plus compliqué !!!
Te Pito o Te Henua - le nombril du monde
Il semble qu'il y a un nom encore plus ancien qui désigne cette ile. Il s'agit de Te Pito o Te Henua, soit le "nombril du monde".
Il y a un lieu de cérémonie nommé Ahu Te pito Kura qui signifie "nombril de lumière". Le nom de nombril met en lien ce lieu et le nombril du monde.
Sur le lieu de Te Pito Kura on trouve le plus grand des Moaï, malheureusement tombé. Et, on trouve surtout une étrange pierre ronde et magnétique. Elle dévie les boussoles !
La légende dit que c'est une pierre source de Mana, l'énergie vitale. Un peu l'équivalent du ch'i (qi) que l'on trouve en Chine ou du Prāṇa en Inde.
La forme de la pierre évoque un oeuf. Notre fameux oeuf de Pâques ?
L'Easter Egg que l'on cherche ?
oui, mais non.. C'est bien un des composants des mystères de cette ile, mais j'ai bien plus étrange et mystérieux à te montrer !!
Une ile qui montre les Solstices et équinoxes
L'ile de MATA-KITE-RANI. Ce qui signifie "des yeux regardent le ciel". Ce qui est suggéré ici dans un univers qui est un langage, dans une conversation qui fait sens, c'est l'astronomie.
Les astronomes regardent le ciel, étudient la mécanique céleste.
Ainsi il n'est pas étonnant de trouver dans le paysage un moyen de marquer les cycles de l'astre le plus important le soleil.
Dans de nombreux lieux on trouve des "calendriers", souvent sous forme d'un rectangle solsticial.
Le rectangle solsticial
Il nous fut faire un petit moment d'explication sur un sujet peu connu, l'astro-géométrie.
Le Solstice est un mot qui signifie soleil qui s'arrête. En effet, si on regarde le coucher de soleil depuis le même lieu, chaque jour il se déplace, mais à un moment il s'arrête et repart dans l'autre sens. Cette position extrême est le solstice.
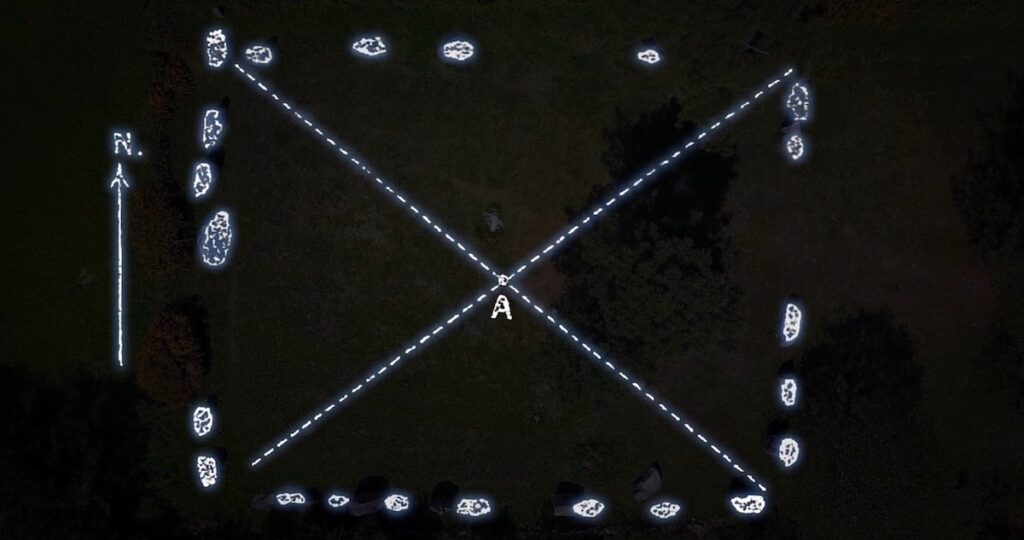
Un rectangle solsticial est utile pour marquer par ses diagonales les solstices.
On ne retrouve pas partout des rectangles solsticiaux, car il ne sont généralement présents que sur les lieux intéressants pour l'astro-géométrie.
L'astro-géométrie, mélange le marquage au sol des cycles astronomiques (ce qui est en bas est comme ce qui est en haut) ainsi que la géométrie sacrée. Soit une géométrie qui s'intéresse à certaines formes géométriques plus fécondes. (proportion dorée, carré, double carré, racine carrée, racine de 3, racine de 5, triangle 3-4-5, etc...)
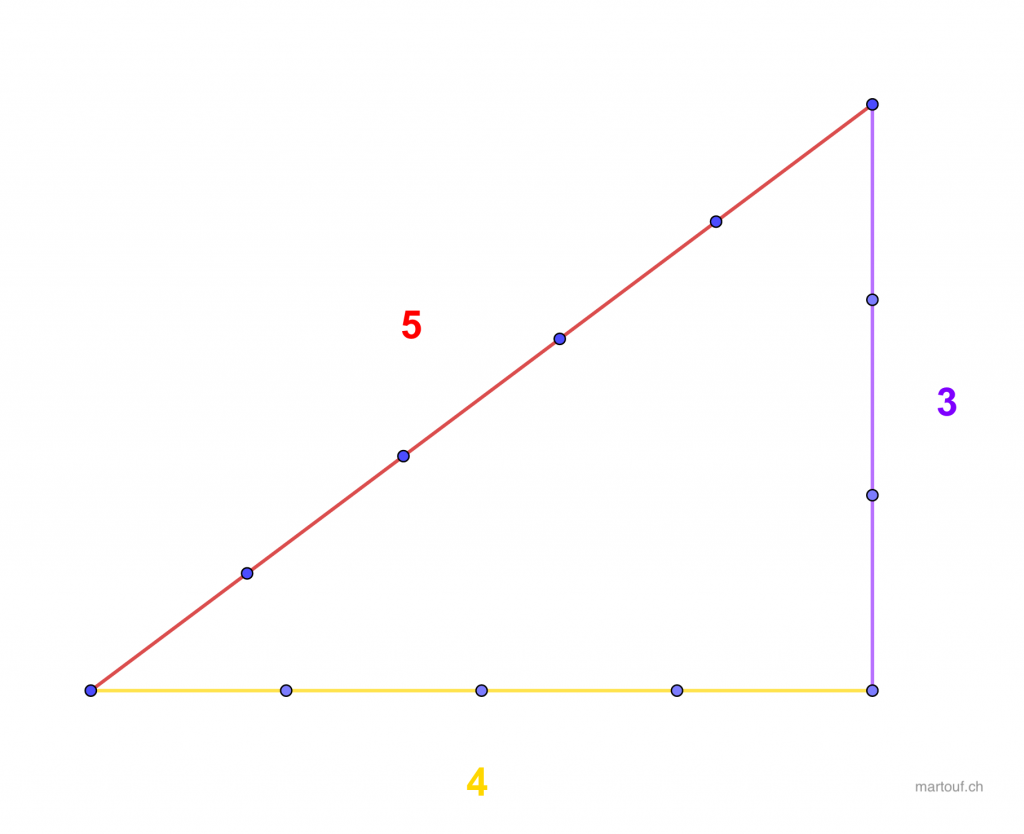
Il se trouve que le rectangle solsticial de Crucuno a la proportion d'un triangle rectangle 3-4-5, le premier des triangles rectangles. (souviens toi du thèorème de Pythagore)
Il faut bien insister sur le fait qu'un tel rectangle solsticial en forme d'un triangle 3-4-5 n'est possible qu'à une latitude particulière.
Il se trouve qu'en -4000, date de la construction des mégalithes de Crucuno, la latitude est celle de Carnac.
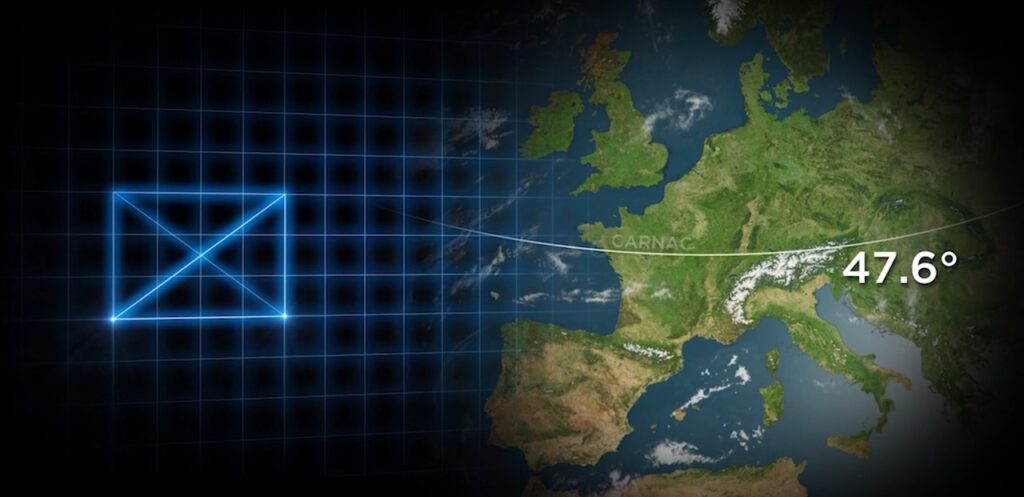
A d'autres latitudes particulières on trouve d'autres formes géométriques issues de la géométrie sacrée. Voici un exemple de formes courantes:

Si on cherche à quelle latitude les axes des solstices forment un double carré on tombe sur un lieu connu en égypte... Karnak !

Ainsi on trouve à Carnac un rectangle solsticial 3-4-5,
et on trouve à Karnak un rectangle solsticial d'un double carré.
Encore une fois, ici l'univers nous montre un lien de sens entre des lieux qui ont le même nom et sont bâtis sur le même principe d'astro-géométrie.
Mais attention oser dire ça, c'est s'attirer les foudres des zététiciens. Mais je le rappelle, l'univers est avant tout un langage !
Bon... et alors pour l'ile de Pâques ?
Solstices de l'ile de Pâques
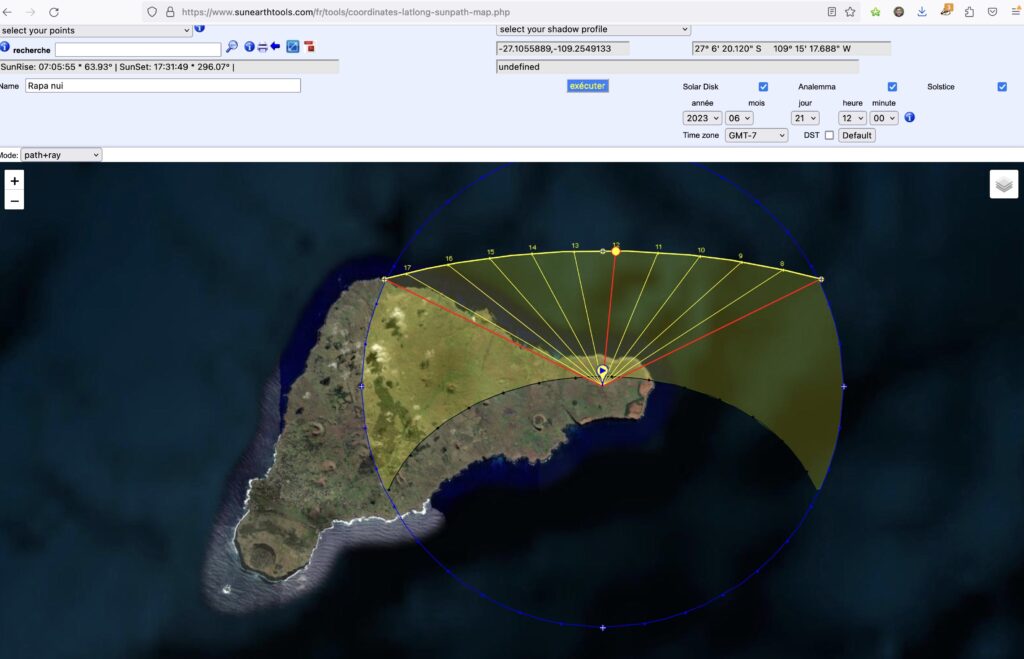
Je me suis rendu sur le site sunearthtools.com pour aller chercher la position des axes du soleil durant les solstices.
J'ai positionné mon point d'observation sur ce qui me semblait un des points les plus intéressants de l'ile, c'est à dire un sommet, celui du volcan Poike.
Le sommet le plus à l'ouest de l'ile de Pâques. Ce qui permet d'admirer les levers et couchers de soleil.

Je constate que lors du solstice d'hiver (en juin, c'est bizarre on est dans l'hémisphère sud, j'ai pas l'habitude !) le soleil se lève sur la mer le matin et se couche dans l'axe de la côte le soir.
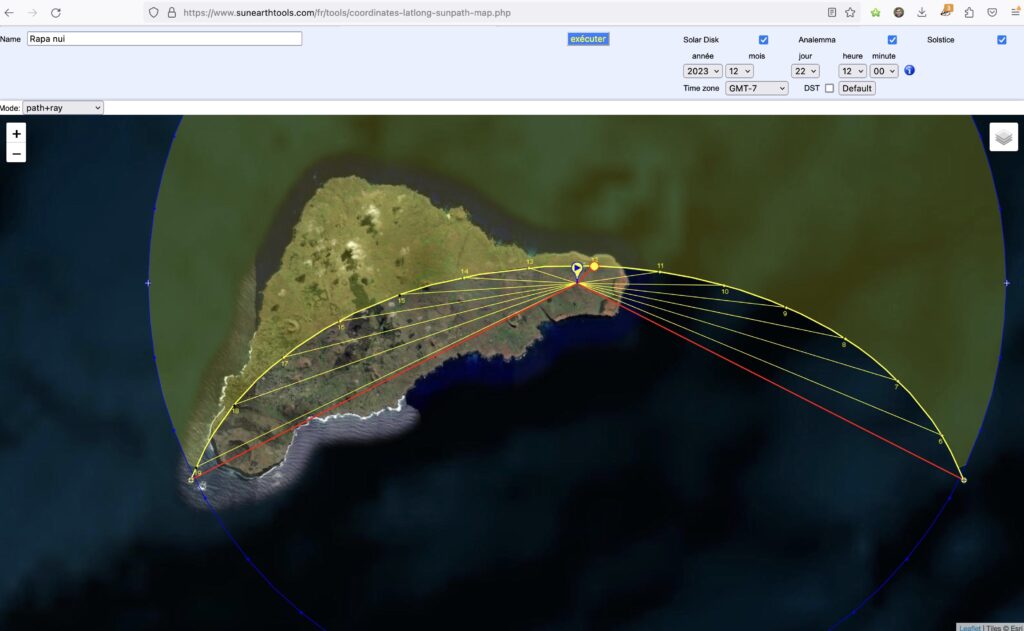
Au solstice d'été (en décembre), je constate que depuis le même volcan Poike, le soleil se lève sur la mer, à l'opposé du coucher de soleil du solstice d'hiver.
Puis le soleil se couche sur l'axe de la plus longue des côtes de l'ile. Pile poil dans l'axe du centre du volcan Rano Kao qui est à l'opposé à 20km de là.
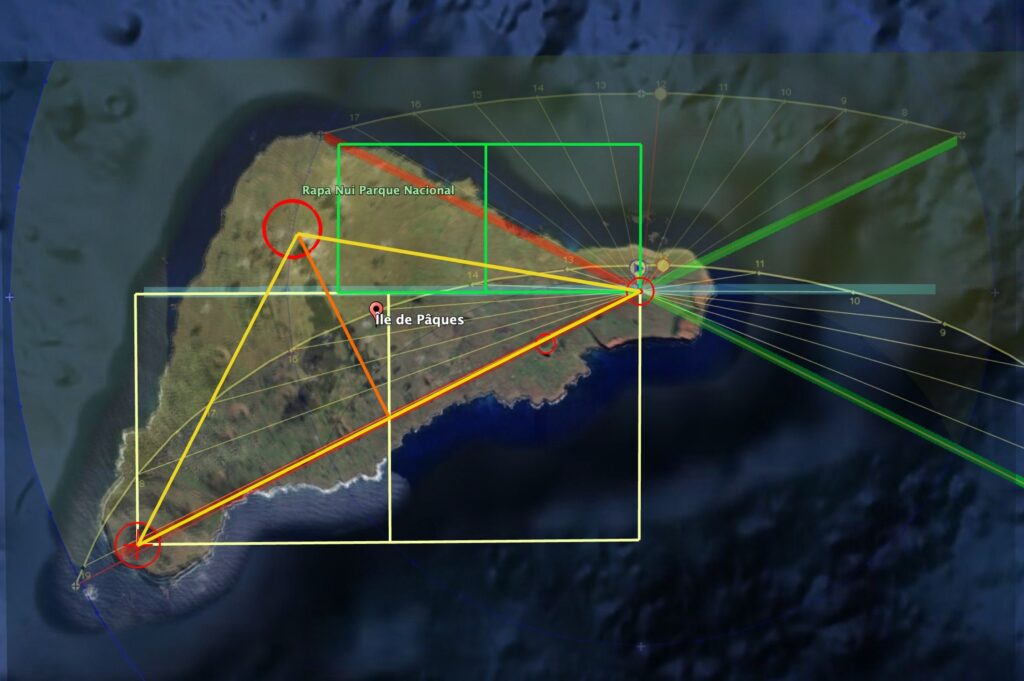
Puis j'ai mis tout ça sur la même image:
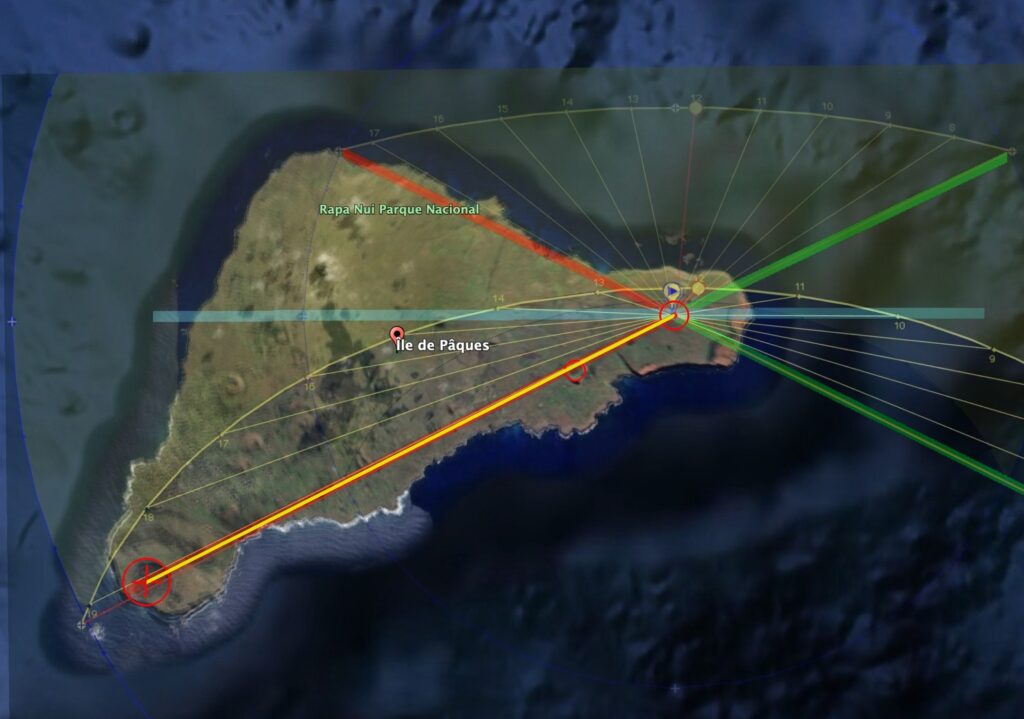
Donc on a ici un rectangle solsticial d'un genre tout à fait particulier. C'est les contours de l'ile qui semblent marquer les axes des solstices !!!
Est-ce que ces axes sont le reflet d'une géométrie particulière ?
→ et bien oui !!
Les axes sont posés sur la diagonale d'un double carré !
Cette forme est très courante en géométrie sacrée, on la trouve dans le profil de la pyramide de khéops, mais aussi comme forme du sol de la chambre de Khéops et comme angle d'inclinaison des couloirs !
J'ai aussi vu le double carré comme forme de base des alignements de menhir de Clendy. Ceux-ci daté de -4000.
Cette forme en double carré, est la porte ouverte vers le dessin de la proportion dorée, le fameux nombre d'or.
Donc là, on a la confirmation que l'astro-géométrie entre en compte sur l'ile de Pâques.
Comment des gars à moitié à poil ont pu faire ce genre de construction ? Mystère ! (même si nos amis zététiciens trouvent que c'est facile de mettre des diagonales de carrés..)
... et c'est pas fini, on va en ajouter une couche (et 2.. et 3... et.. 4...)
Géométrie de l'ile de Pâques
Tout comme Hawaï ou l'Islande, l'ile de Pâques est passée au dessus d'un point chaud. C'est un point fixe sur la Terre d'où sort du magma. L'écorce terrestre glisse et généralement on observe un chapelet d'iles en lignes.
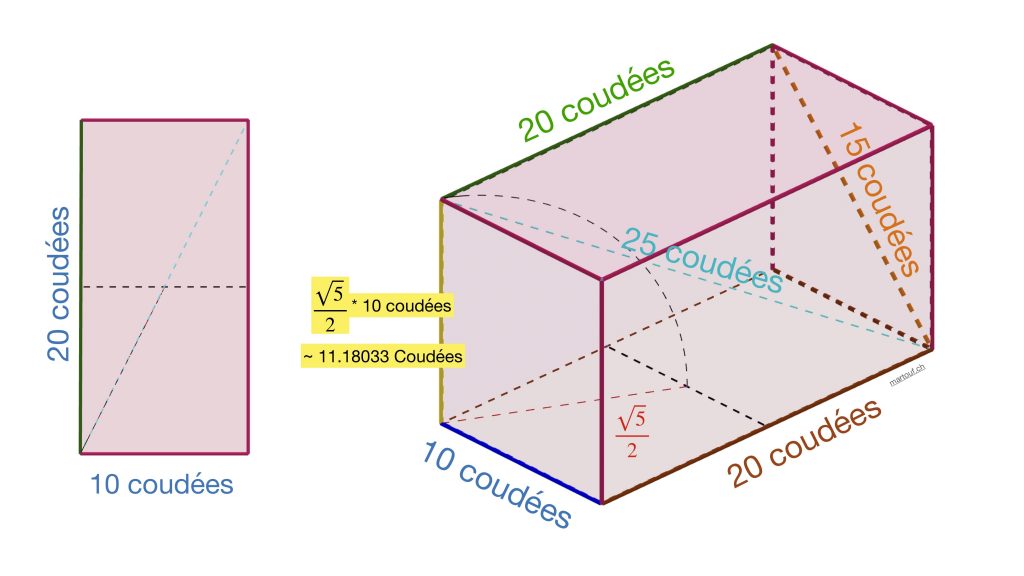
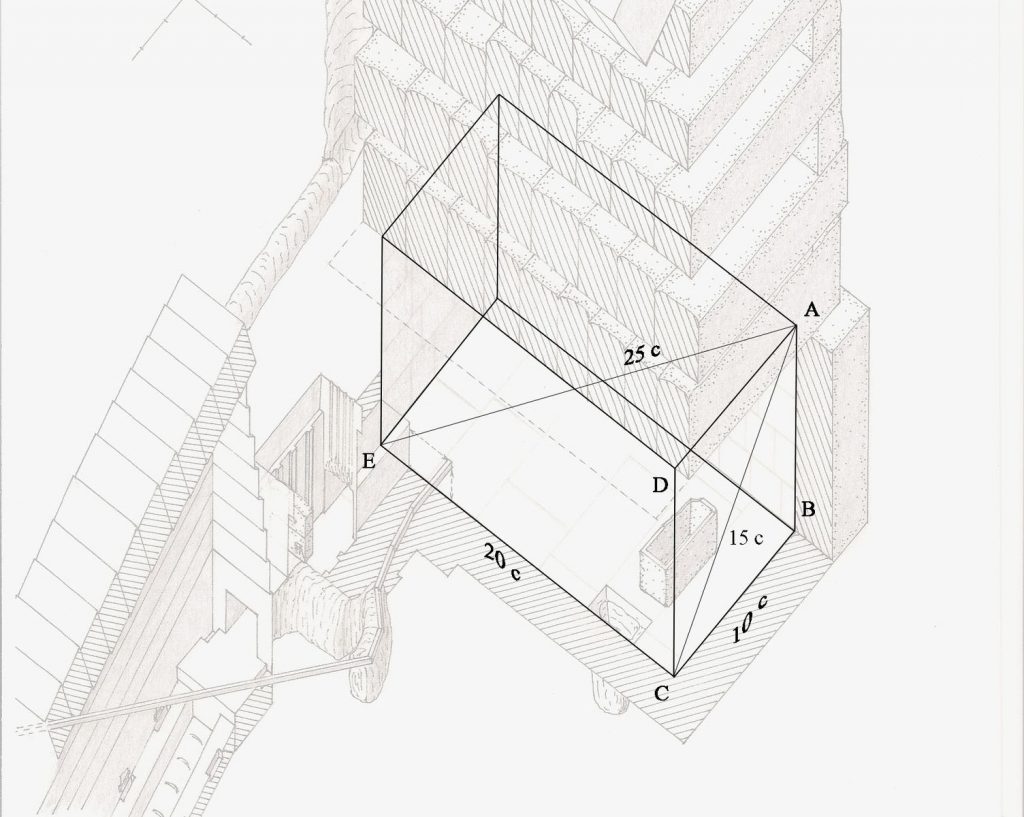
L'ile de Pâques a été formée par 3 volcans:


L'ile de Pâques a la forme d'un triangle isocèle.
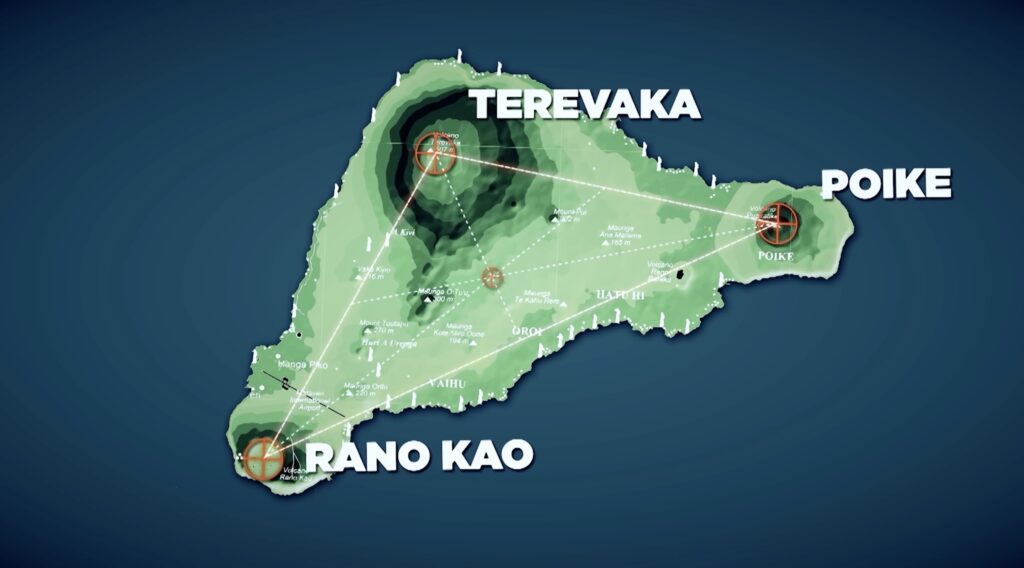
- Il y a exactement 20km entre les volcans Poike et Rano Kau.
- Il y a 12,36 km entre les volcans Poike et Terevaka.
- Il y a 12,36 km entre les volcans Rano Kau et Terevaka.
Les gars à moitié à poil, en plus de tailler des Moaï, ils ont aussi taillé l'ile ?
C'est complètement fou !
En plus des proportions, des nombres significatifs
Donc il y a 20km entre Poike et Rano Kao. Cette ligne marque l'axe du coucher de soleil au solstice d'été.
Les nombres 20 et 12,36 ne sont pas anodins. Il y a entre eux un rapport qui vaut le nombre d'or !!
12,36 * 1,1618 = 20
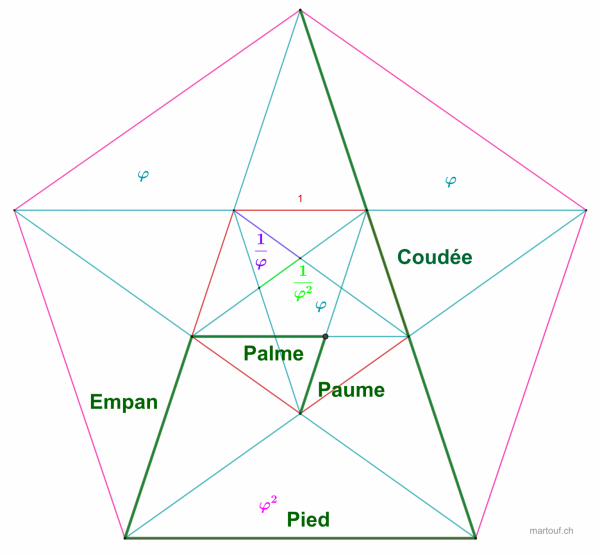
Il se trouve que j'ai déjà beaucoup parlé de ces rapports. Car c'est tout simplement ceux utilisés dans la quine des bâtisseurs.
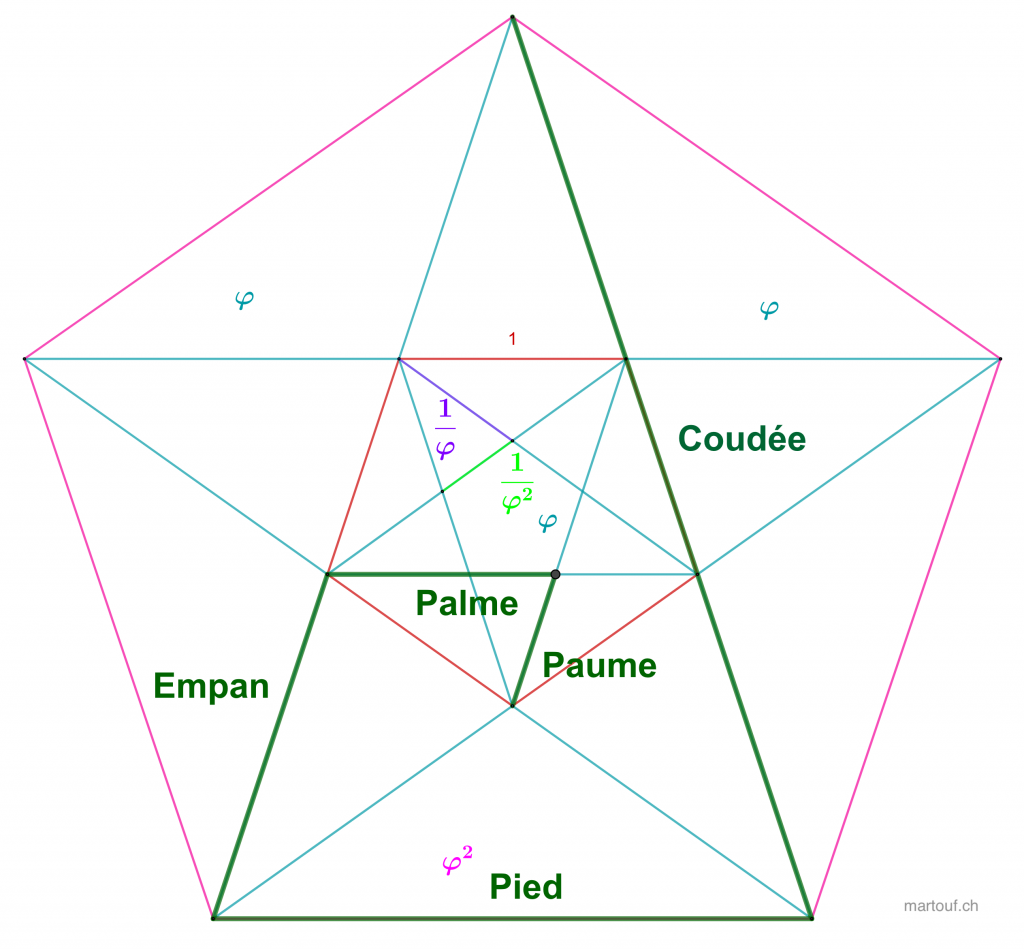
C'est un système de mesure qui relie grâce au nombre d'or des mesures diverses:
- paume : 7,64 cm
- palme : 12,36 cm
- empan : 20 cm
- pied : 32,36 cm
- coudée: 52,36 cm
Ceci est basé sur la géométrie d'une étoile à 5 branches.
Le triangle isocèle entre les 3 volcans de l'Ile de Pâques s'inscrit totalement dans cette géométrie qui transpire le nombre d'or.
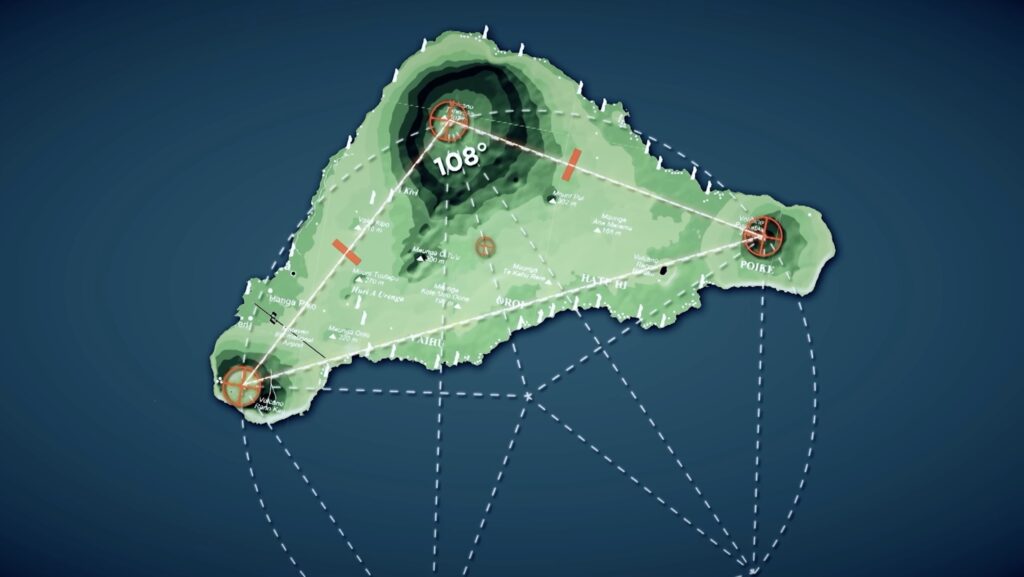
Peu de gens réalisent vraiment ce que ça signifie ce genre de "coïncidences".
Petit récapitulatif, on a:
- un axe des solstices avec un angle particulier, donc possible qu'à une latitude particulière
- ce même axe constitue la base d'un triangle isocèle entre 3 volcans.
- En plus des dimensions, il y a la taille avec des valeurs numériques significatives qui transpirent le nombre d'or.
- Ces valeurs sont exprimées en mètre !
Donc là pour moi on est bien au delà des discussions courantes en archéologie de savoir comment les Moaï ont été transportés !
Là on est en train de dire que l'ile a été positionnée à un endroit précis en fonction de contraintes précises, ainsi que "taillée" dans une géométrie précise !
Qui peut faire ça ?
... et on va encore en ajouter des couches !!
Surface de l'ile de Pâques
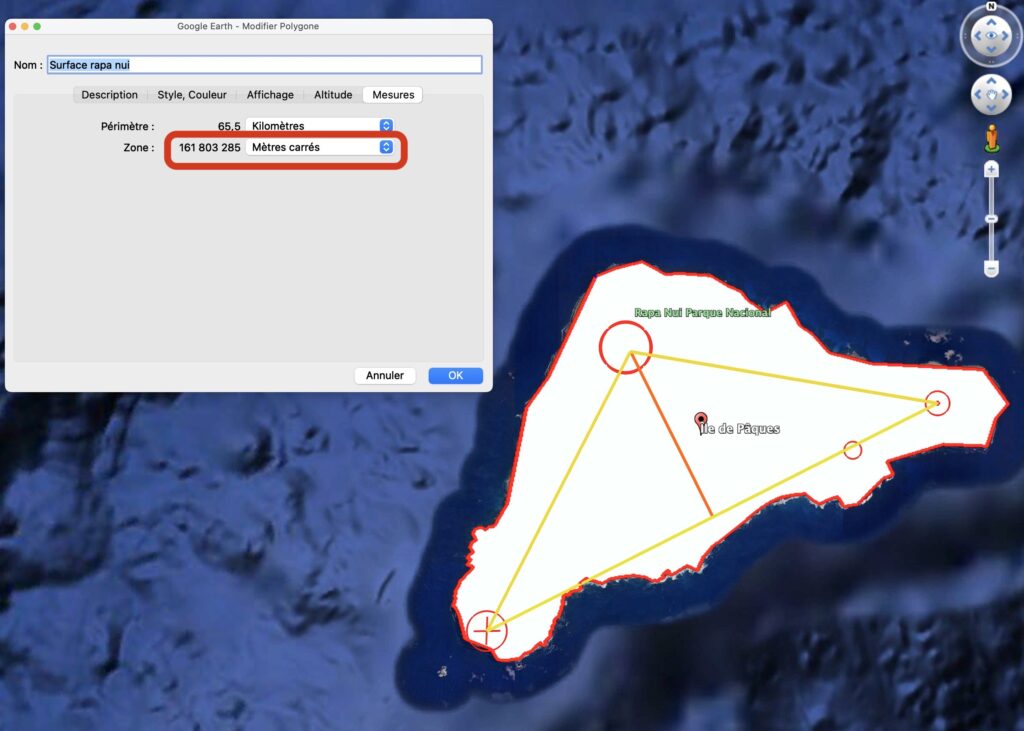
J'ai mesuré dans Google Earth la surface de l'ile de Pâques.
J'arrive à une résultat de 161 803 285 mètres carrés.
Encore une fois, on un nombre qui a du sens, on peut y voir le nombre d'or: 1.6180339887...
Je vois mal comment avec toutes les contraintes déjà citées, on peut ajouter encore le fait d'avoir une surface qui signifie le nombre d'or !?
Pour moi là, on est dans un langage. L'univers signifie le nombre d'or.
Alors il est temps de monter un autre exemple en poussant encore plus loin la notion de langage.
Polarités des éléments et distance dorée
Dans l'esprit de la philosophie hermétique nous allons utiliser les polarités comme langage.
L'ile de Pâques est une ile volcanique.🌋
- C'est donc une ile de roche issue du feu.🔥
- Cette ile est perdue au milieu d'un désert d'eau. 💧
- L'ile de Pâques est l'endroit habité le plus isolé au monde.
- L'ile est posée sur le Fond marin le plus jeune de la planète.
On va inverser les polarités pour voir ce que ça donne. On va chercher:
- Un lieu central dans le monde.
- Le fond marin le plus vieux.
- Un désert sec 🐪
- Une roche d'eau,💧 soit du calcaire, une roche sédimentaire composée dans l'eau. Autrement dit de la pierre-humide → pyramide ?
Si on met ensemble tout ces critères, on arrive où ?
→ Sur les pyramides de Gizeh, conçues en calcaire, sur le lieu qui est le centre des terres émergée habitables. (le habitable est important !)
Les pyramides sont aux portes du Sahara, un désert sec.
La carte des fonds marins nous montre que la méditerranée orientale est le fond marin le plus ancien de la planète.
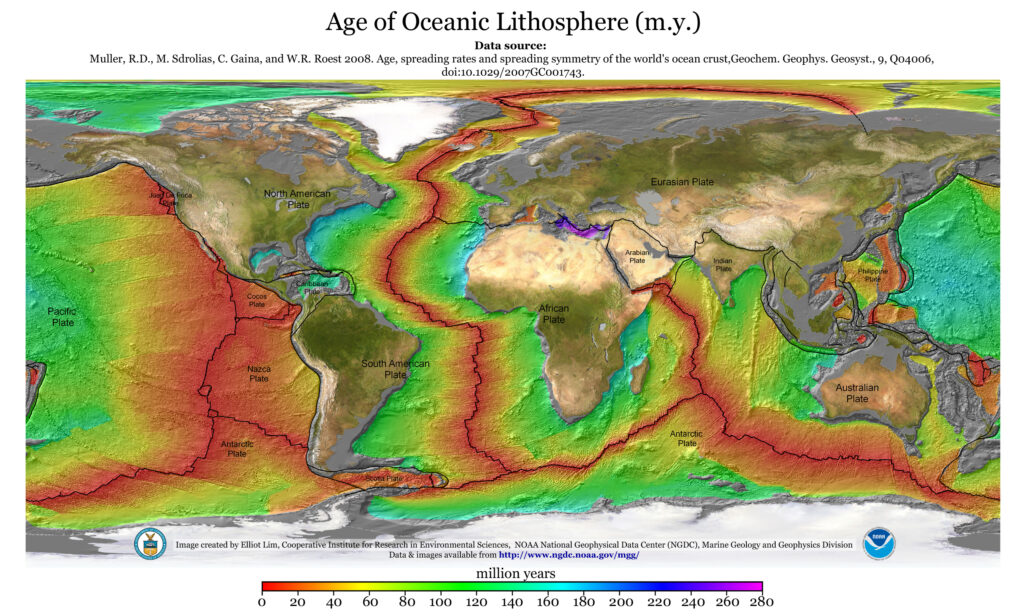
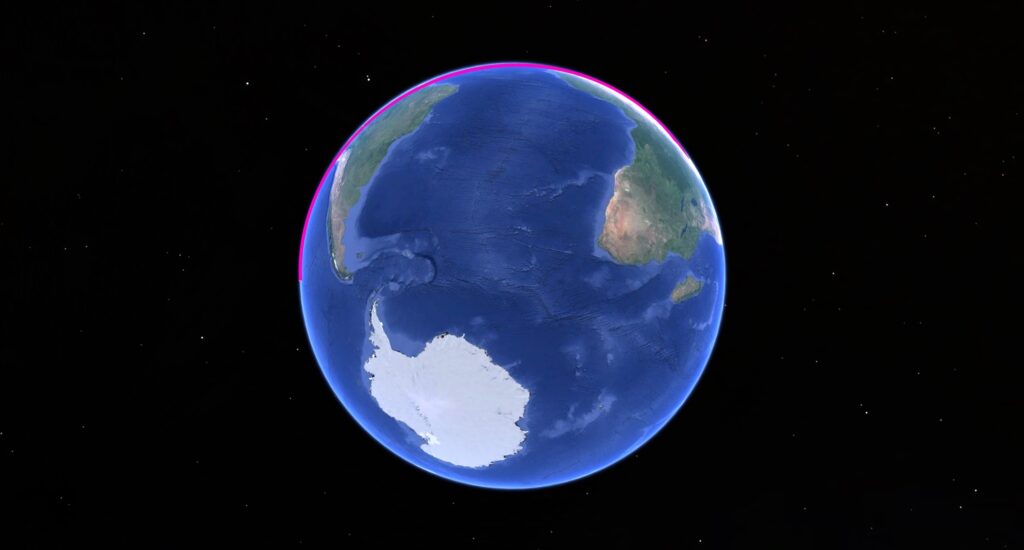
Donc voilà, pour bien visualiser la chose, voici une vidéo qui met en lien ces deux lieux: Rapa Nui et Gizeh.
Dans le domaine de l'archéologie interdite et des chercheurs alternatifs on a ceux qui pensent qu'une ancienne civilisation disparue a construit les monuments les plus étranges de notre planètes.
Et il y a ceux qui pensent que ce sont des extra-terrestres qui ont été les bâtisseurs de ces lieux. (pyramide de Gizeh, ligne de Nazca, ile de Pâques, Angkor Vat, pyramide de Chine, etc...)
Je vois mal comment une civilisation humaine ou même extra-terrestre pourrait terraformer la planète pour faire joujou ??
Avec quel outils ?
Pour moi, ce n'est ni une ancienne civilisation, ni des extraterrestres, on a autre chose !
Pour moi on a là un langage.
Si on mesure bien précisément la distance depuis le sommet de la pyramide de Khéops on arrive pas directement sur l'ile de pâques, mais sur l'ilot de Motu Nui.
→ Ah ben voilà la preuve que ça marche pas ce truc...
→ T'es sceptique ? ... alors regarde la distance entre Rapa nui, et Motu nui...
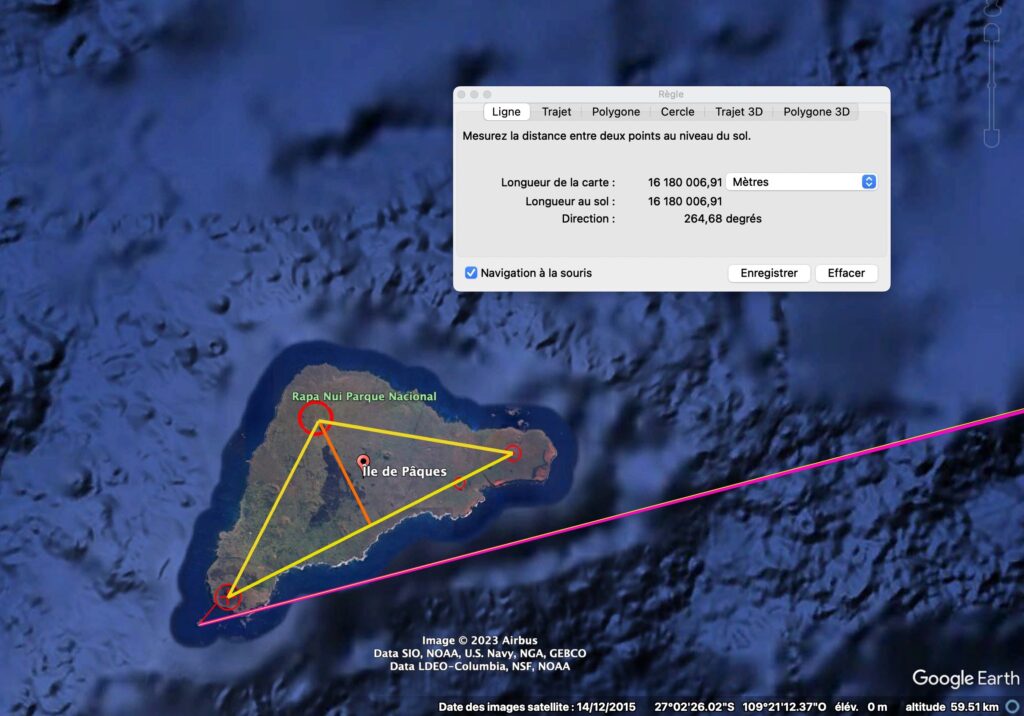
Il y a exactement 1618 mètres entre Orongo – le centre de cérémonie du dieu Make Make – et le centre de l'ilot de Motu Nui.
Tout collé à l'ilot de Motu nui, il y a l'ilot Motu iti qui a une surface de 1,6(18) hectare !
En chemin, il y a un petit ilot poitu – Motu Kao kao – qui lui est à exactement 1000m de Orongo !
Encore un coup des gars à moitié à poil qui ont posé cet ilot à la bonne distance !
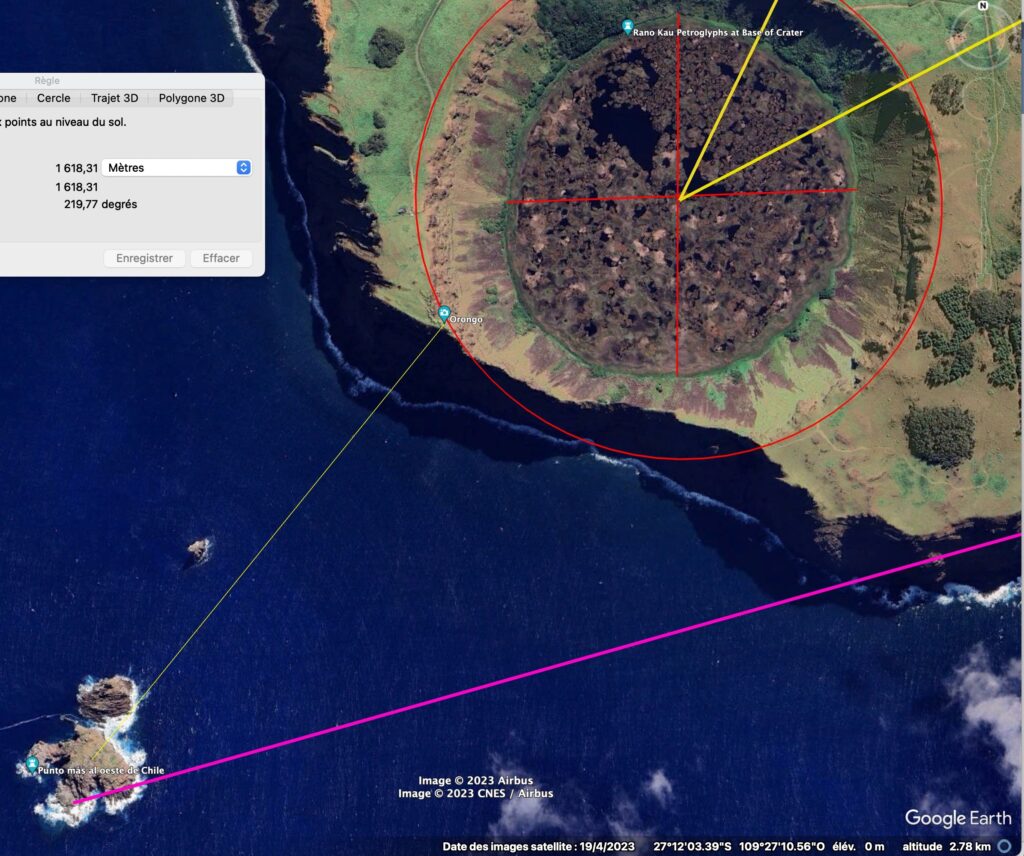
Plusieurs variantes de la distances Gizeh - Ile de Pâques
Pour être transparent, il est temps d'ajouter quelques précisions.
Ce n'est pas moi qui ai découvert que la distance Gizeh - Ils de Pâques faut 10 000 fois le nombre d'or.
Je ne sais pas qui a découvert ceci en premier. Mais la première fois que j'en ai entendu parlé, c'était dans le film "La révélation des pyramides".
Mais je n'y ai pas fait attention tout de suite. Il y avait tellement d'info en même temps.
Donc c'est aussi pour ça que je t'épargne encore de nombreuses bizarreries à propos de l'ile de Pâques.. mais si tu veux creuser c'est par ici...
Puis Patrice Pouillard a fait le film BAM, et il a repris ce qu'il avait mis dans LRDP, mais en affinant la distance pour montrer un lieu précis. Là il montre le centre de l'ile. (à 1h41... soit racine de 2 !)

Il montre que dans l'app https://maps.me la distance est de 16180km au centre de l'ile. Alors que Google earth indique la même distance plutôt sur l'ilot à l'est de l'ile.
Il y a deux variantes ? ... et oui, tout dépend de la méthode de mesure.
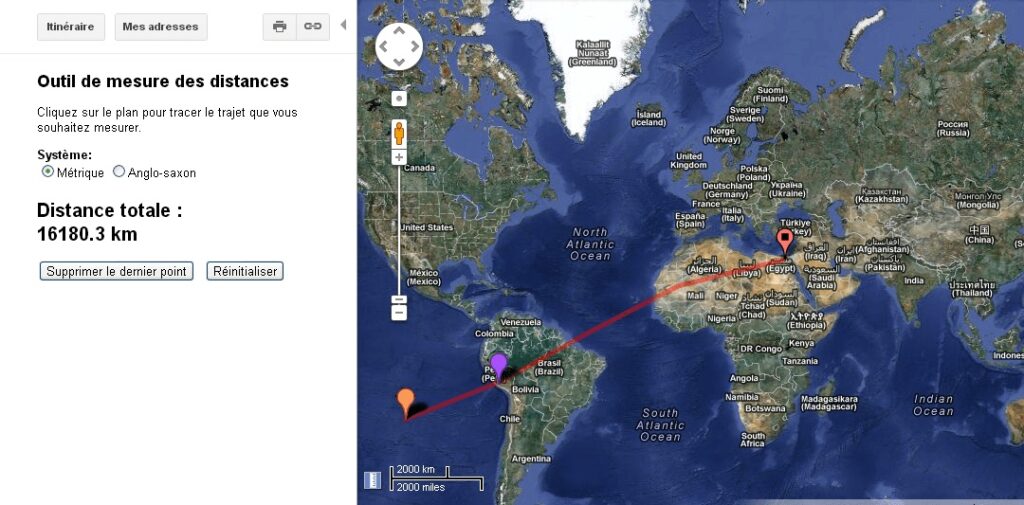
Quentin Leplat avait déjà montré ceci dans un article. Il avait lui même vérifié les affirmations vue dans LRDP en 2012. A l'époque il avait simplement demandé à Google Maps la distance entre Gizeh et l'ile de Pâques. Résultat en 2012: 16180,3 km.
Puis en 2014, mise à jour ça donne plus le même résultat. Il vérifie avec Google Earth qui est plus précis, et en effet, ça ne marche plus pour le centre de l'ile.
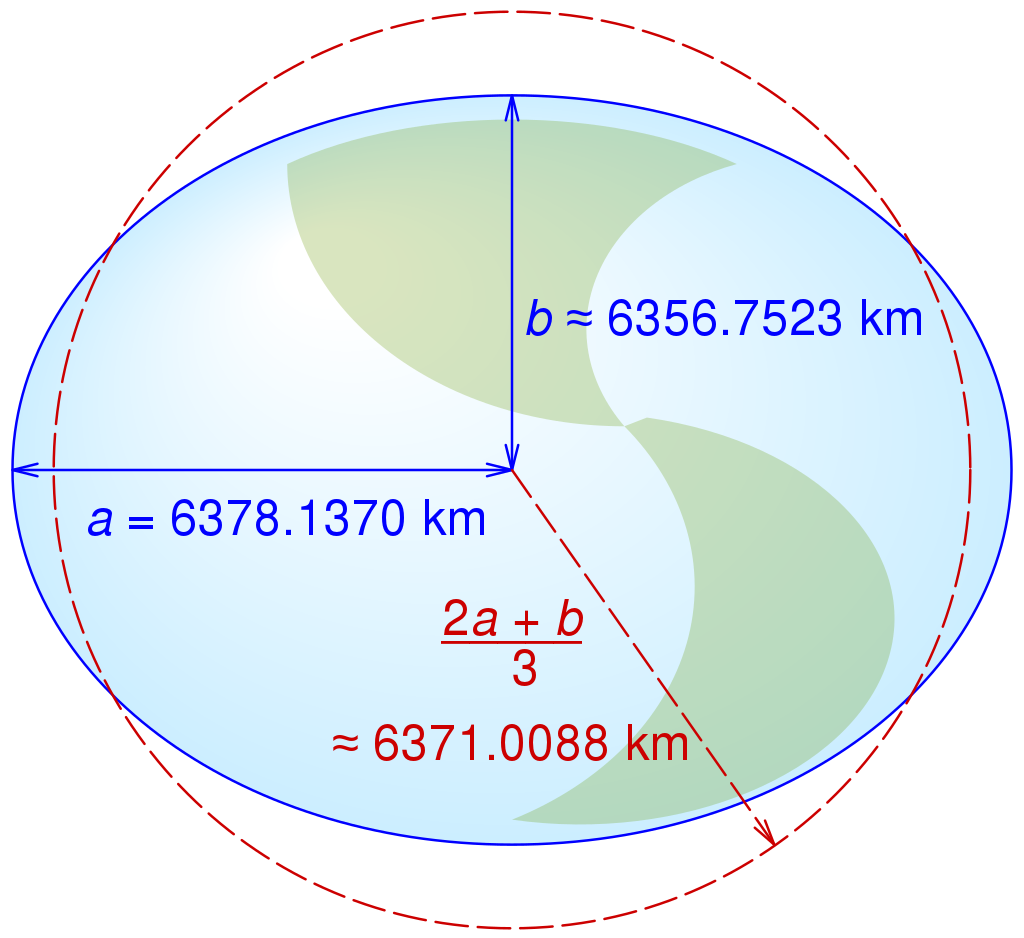
Quentin cherche donc une explication. Et il la trouve. La terre n'est pas une sphère parfaite. (ouais, elle pas plate.. mais elle est pas ronde non plus !)
La Terre n'est pas non plus une ellipsoïde comme le pensaient les concepteur du mètre lors de la révolution française. La Terre est irrégulière. La figure de la Terre –comme on dit dans le jargon– est un géoïde.
Donc pour être précis, il faut un modèle de la Terre, on fait un maillage en triangles, pour créer un système géodésique. Le système global le plus utilisée, celui du GPS est le modèle WGS84.
Suivant les applications utilisées, on utilise un modèle de la Terre plus ou moins simple.
En 2012, google maps utilisait un modèle simple. La terre est vue comme une sphère de rayon moyen volumétrique de 6371 km. C'est tout à fait pertinent pour un système qui veut juste t'indiquer comment te rendre d'un endroit à un autre d'une ville !!
Mais quand on veut mesurer une distance d'un bout à un autre de la planète, on va utiliser un modèle basé sur une ellipsoïde. C'est ce qui a été changé en 2014.
Donc voilà comment on arrive à deux résultats différents.
Alors tu peux le prendre à la façon zététicien, tout ça c'est du hasard, des coïncidences, aucun des modèles géodésiques n'est significatif.
Ou alors, tu peux le voir comme moi, comme un langage. Personnellement je trouve que les deux modèles sont pertinents !!
- Le centre de l'ile en modèle simple: la terre est une sphère.
- L'ile de Motu nui en modèle ellipsoide: car la mythologie qui y est liée est hallucinante. On en parle juste après ci-dessous.
Les deux version ont du sens ! C'est un langage spatio-temporel !
Quelques chose d'aussi figé qu'une distance peut changer dans le temps ! ou du moins notre perception. Donc pour moi ça nous montre un langage qui est justement adapté à l'observateur, ici et maintenant.
Mon pote Mr137 nous a aussi montrée que l'on a des alignements conçus pour fonctionner en ligne Loxodromique et d'autres en ligne Orthodromique.
Soit en projection à plat pour une carte papier, ou en mode géodésique sur une courbe. 📐🌍
C'est que l'on constates avec les lieux nommé "le Caire" ou "les Caires" en France.
On est dans un langage polarisé comme vu ci-dessus !
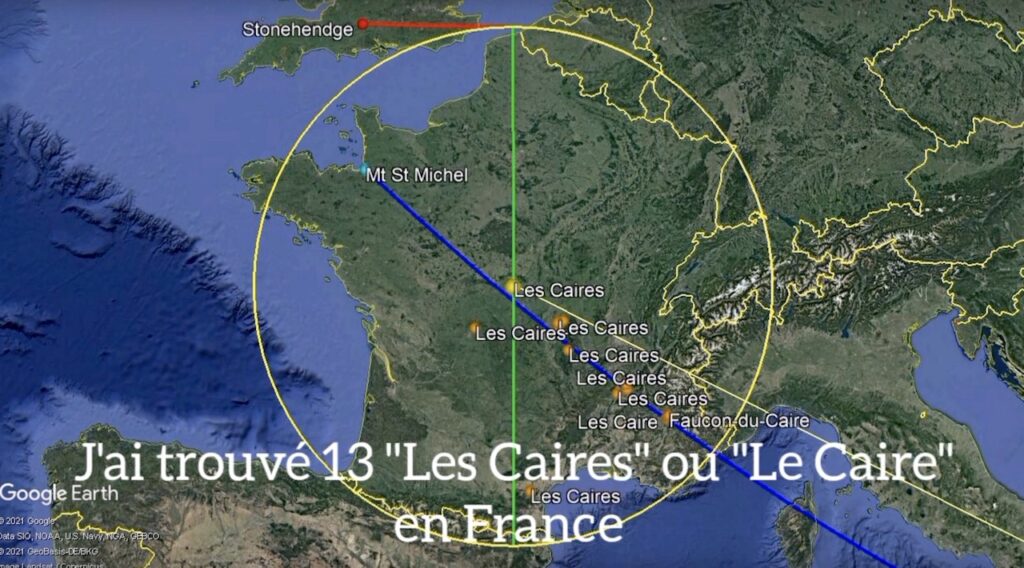
L'oeuf de Make Make 🥚
Il ne faut pas oublier ma quête, celle de la chasse à l'oeuf. La chasse à l'easter egg.
Donc ici on est d'accord que Easter est le nom (actuel) de cette ile mystérieuse.
Mais bon on a toujours pas d'oeuf !
C'est là qu'il est temps de revenir sur l'histoire du dieu Make Make.
Jusque vers 1860 c'est la civilisation matamua qui occupait l'ile et vouait un culte à Make Make. Puis des esclavagistes Chiliens ont changé le cours de l'histoire de l'ile de Pâques en déportant ses habitants et en les remplaçants. Puis la christianisation a eu raison du culte de Make Make.
Selon le mythe fondateur Matamua, le Dieu Make Make est arrivé sur l'ilot Motu nui avec un oeuf qui a donné vie au premier humain.
Donc voilà, on l'a notre oeuf !
Ce petit ilot de rien du tout à côté d'une ile perdue au milieu de l'océan, c'est là qu'est l'origine des humains. C'est là que l'oeuf 🥚 est arrivé.
(le 9, nef, navire, nouveau, néo, noé.. étranges liens, j'ai déjà écrit un article à ce propos...)
Le culte de l'homme oiseau
Pour célébrer la naissance des humains apportés par Make Make dans un oeuf, les matamua célébraient le culte de l'homme oiseau, le Tagata Manu.
(Manu comme le Noé Indien de la religion Védique !)
Depuis Orongo, il faut aller chercher un oeuf de sterne sur l'ilot de Motu Nui
Rien que ça !
Il s'agit de descendre des hautes falaises, de nager 1,618 km dans une mer infestée de requins, de trouver le 1er oeuf de la saison et de revenir avec sans le casser !
Ça c'est de la chasse aux oeufs !

Les Hopu manu – les représentants de chaque clans – pratiquaient ce culte chaque année, ceci jusqu'en 1866, précisément le 22 décembre, soit le solstice d'été !
Ainsi on retrouve l'axe du coucher de soleil au solstice d'été !
Tout se tient !
On l'a notre Easter Egg
Bon alors pour revenir à la quête initiale, à la chasse à l'oeuf de Pâques.
Je crois qu'ici on a trouvé l'Easter egg.
Si j'étais le concepteur de ce monde, j'aurai bien envie de le signer, même si le big boss dit que je n'ai pas le droit.
Donc je place discrètement un easter egg, un clin d'oeil, un truc qui n'a rien à faire dans le jeu "normal".
J'ai bien envie qu'un jour quelqu'un puisse trouver mon easter egg, mais en même temps faut pas qu'il soit visible trop facilement et qu'il ne soit découvert rapidement.
Je vais donc planquer mon easter egg loin de tout.... sur la terre la plus isolée du monde par exemple !
Terra formation
La géométrie, le positionnement, les caractéristiques de l'ile de Pâques sont tellement étrange et complexe à réaliser que je ne vois pas comment on peut concevoir et réaliser un truc pareil.
Je ne ne vois pas comment c'est possible en étant incarné dans ce monde, en ne pouvant utiliser que les maigres moyens à disposition.
Par contre, dans un jeu vidéo, tout est possible. Il y a des jeux à succès qui permettent de créer une cartes, un terrain de jeu en mode éditeur, puis de s'y incarner pour jouer une partie.
Je pense particulièrement à :
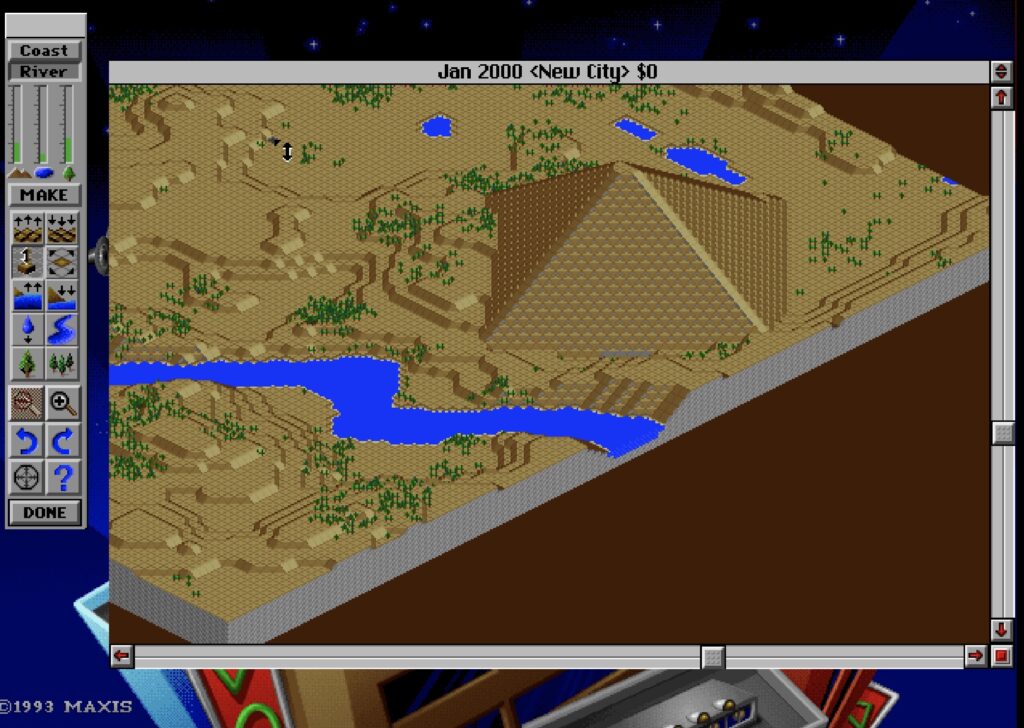
- simCity
- Minecraft
Je me suis d'ailleurs amusé sur simcity 2000 à créé une pyramide. C'est très facile.
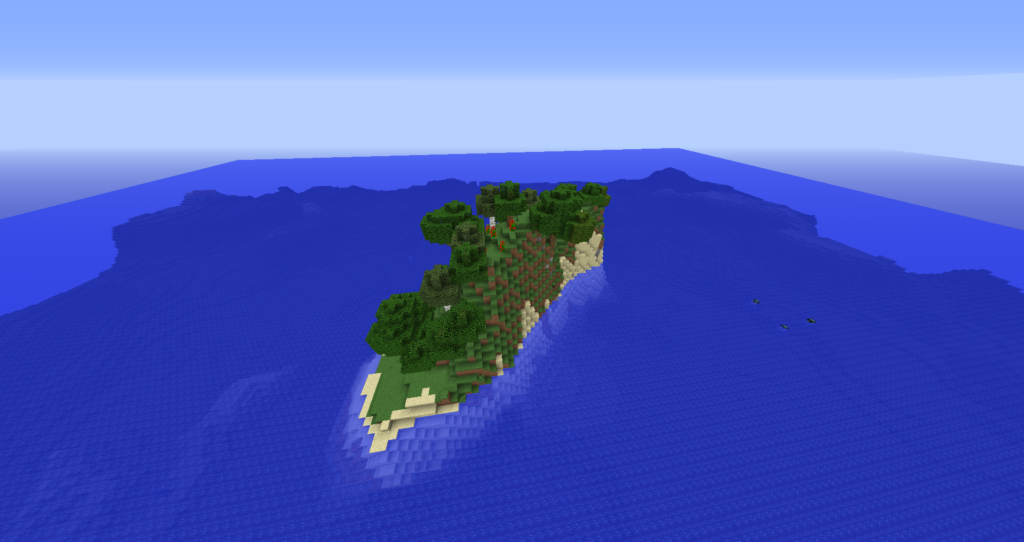
Voici une jolie balade sur l'ile de Pâques en version Minecraft.
Si l'on a envie de créer ce genre de monde à l'intérieur de notre réalité, pourquoi notre réalité ne serait pas une simulation dans une réalité plus vaste ?
On peut même voir les solstices sur minecraft !
Voici donc ce qui me mène à poser l'hypothèse que nous vivons dans une jeu vidéo !
Ça me semble l'hypothèse la plus rationnelle. Je vois mal des gens, même une civilisation avancée perdue dans le passé, se mettre à créer une ile de toute pièce comme une oeuvre d'art. Il y a trop de paramètres.
Ainsi le plus simple, c'est de se questionner sur la nature de la réalité !

Inspiration non-terrestre
Dans une émission sur ado-fm en décembre 2012, le clairvoyant Christophe Allain a donné son point de vue sur les mystères de l'ile de Pâques vu qu'il y est allé.
Il dit que les constructions sont humaines, réalisés par des humains. Mais que les instructions, les inspiration viennent d'ailleurs. Il parle d'énergie extra-terrestre. Mais pour lui ça n'a pas le sens des petits hommes verts ou gris.
"énergie extra-terrestre" est pour Christophe Allain, tout ce qui vient d'ailleurs de la terre. (c'est bien ce que ET veut dire !)
C'est en fait très courant, de nombreuses inspirations chez toutes sortes de personnes, de l'artiste au scientifique provient souvent d'ailleurs...
De où exactement on ne sait pas. Il évoque que tout est possible. Ça peut même être une personne qui rêve un monde et lui donne ainsi vie. On rejoint l'idée de Tchouang-tseu, un des fondateur du taoïsme.
Perso, en étudiant la nature du temps et la théorie de la double causalité, dans laquelle le futur est réalisé et informe le présent, je me dis qu'il est aussi tout à fait plausible que nos descendants nous suggèrent des informations depuis le futur, afin de créer une boucle spatio-temporel créative.
Par exemple des gens du futur peuvent créer des monuments dans le passé avec des dimensions en mètre...
Si tu ne comprends pas ce que je dis, il est temps de lire les BD d'imbattable, et après les boucles spatio-temporelles créatrices n'auront plus de secret pour toi.

On pourrait imaginer le contraire en suivant le conditionnement du passé pour former un futur pessimiste.
Donc imagine un chamane qui se connecte à d'autres dimensions et reçoit des infos du futur pour construire une structure qui fera grandir l'humanité et l'amener dans le futur d'où l'idée vient. (et pas un autre)
Pour d'autres exemples je t'invite à lire mon article:
Retour vers le futur n'est pas une fiction....

D'ailleurs Christophe Allain mentionne aussi ce genre d'influence bouclée du futur sur le passé pour se créer elle même un bon futur.
Ça m'évoque l'histoire de 2001 Odysée de l'espace, avec le monolithe qui apparait aux moments clé de l'Histoire de l'Humanité.
A méditer.