Aujourd'hui, je vais te parler du nombre d'or.
L'article wikipedia sur le Nombre d'Or étant déjà jugé comme un bon article, pour éviter de réinventer la roue, il est déjà possible de se référer à cet article , mais j'avais envie de présenter ce nombre à ma manière. De mettre en avant ce qui m'intéresse moi dans ce nombre. C'est à dire surtout une structure fractale du monde qui me questionne. Et surtout, ce qui ne passe pas sur wikipedia, l'utilisation du nombre d'or comme système de mesure universel, très ancien, et même liée au mètre !
Cet article est une base amenée à évoluer, tellement le sujet a du potentiel à se développer. J'ai également écrit un article à propos de la Géométrie sacrée pour expliquer le mode de pensée des anciens bâtisseurs.
Le nombre d'or est fréquemment représenté par la lettre grecque Phi, Φ, φ, (Suivant la fonte utilisée on voit 2 caractères différents ici)
Définition du nombre d'or
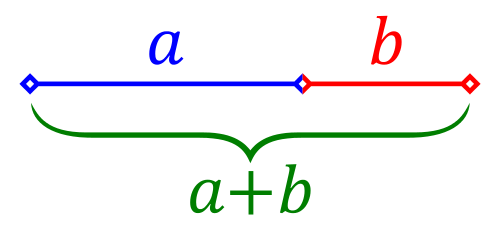
Le nombre d'or est une proportion, définie initialement en géométrie comme l'unique rapport a/b entre deux longueurs a et b telles que le rapport de la somme a + b des deux longueurs sur la plus grande (a) soit égal à celui de la plus grande (a) sur la plus petite (b).
C'est à dire lorsque (a+b)/a = a/b
Voici la même définition avec d'autres mots: Trois points alignés, déterminant deux segments forment une section dorée (un rapport égal à Phi), s'il y a de la petite partie à la grande, le même rapport que de la grande au tout.
Le nombre d'or est le seul rapport qui met en résonance la partie avec le tout. On peut donc le voir comme étant une résonance (fractale) entre la créature et son créateur.
C'est pour cette raison que ce rapport est souvent appelé: La divine proportion.
On peut construire ce rapport dans un rectangle d'or. (le format carte de crédit !)
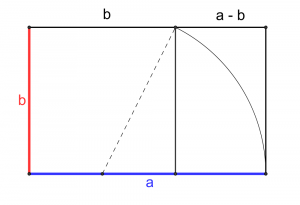
La construction s'effectue en construisant un carré. Puis en piquant un point au milieu du côté du carré. Là on place son compas. On l'ouvre sur la distance au coin et on obtient ainsi une longueur de côté qui permet de faire un rectangle d'or.
Valeur du nombre d'Or
Les anciens, et les visuels, préfèrent faire des mathématiques à travers la géométrie. Il est possible de faire de nombreuses choses acec juste une équerre et un compas. Mais le monde actuel préfère rendre les mathématiques abstraites en usant et abusant d'algèbre. Qui est capable de se représenter ce qu'est une racine carrée ? Et bien c'est tout simplement la longueur de la diagonale d'un carré !
Donc observons le nombre d'or dans une vision algébrique des mathématiques.
Le nombre d'or φ est irrationnel. Il est l'unique solution positive de l'équation x² = x + 1. Il vaut exactement (1+√5)/2
Soit environ 1.6180339887...
Un nombre irrationnel est un nombre qu'il n'est pas possible de réduire en ratio, soit en fraction. Contrairement à π, φ n'est pas un nombre transcendant (un nombre transcendant n'est racine d'aucune équation polynomiale)
φ est un rapport naturellement présent dans de nombreuses constructions géométriques.
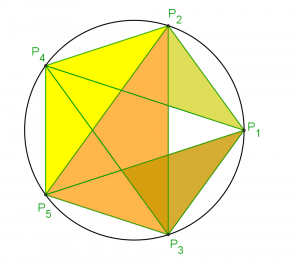
Le pentagone, et l'étoile à 5 branches est une source sûre pour trouver le nombre d'or.
Observe, on y voit un grand triangle isocèle qui point p2 depuis p5 et p3. On voit également le même triangle à une échelle différente. C'est la définition d'une fractale, l'auto-similarité. C'est le petit triangle isocèle qui point p2 et fait avec la ligne p4 - p1 qui coupe le grand triangle isocèle. En bref, une des branche de l'étoile.
Chaque branche de l'étoile est en fait un triangle d'or. Si l'on divise la longueur du grand côté par le petit on obtient le nombre d'or φ.
On a donc ici un rapport φ dans la construction des triangles d'or. Mais il y a 2 niveaux de triangle. Et si l'on compare les longueurs des côtés de ces triangles d'une échelle à l'autre, c'est aussi φ qui ressort !
Équations remarquables
On peut déduire plusieurs particularités de l'équation x² = x + 1 dont la solution et φ et vaut (1+√5)/2:
φ² = φ + 1 ≈ 2.6180339887
1/φ = φ - 1 ≈ 0.6180339887
√5 = φ + 1/φ ≈ 1.6180339887 + 0.6180339887 ≈ 2.236067977
C'est marrant, on peut mélanger les multiplications et les additions !! ... un peu comme le but des logarithme qui nous permet avec des additions de gérer des multiplications. (le principe de la règle à calcul)
Progression géométrique et arithmétique
Grâce aux équations remarquables ci-dessus, le nombre d'or est certainement le seul nombre pour lequel on peut faire coïncider une progression géométrique et une progression arithmétique.
| x-3 | x-2 | x-1 | x0 | x1 | x² | x3 |
|---|---|---|---|---|---|---|
| 1/φ3 | 1/φ² | 1/φ | 1 | φ | φ² | φ3 |
| 0.235 | 0.382 | 0.618 | 1 | 1.618 | 2.618 | 4.236 |
La progression géométrique s'obtient en augmentant la puissance (comme sur l'exemple théorique de la première ligne. La deuxième ligne montrant concrètement ce que ça donne dans le cas de Phi) Le résultat approché est indiqué en notation à virgule sur la troisième ligne.
La progression arithmétique s'obtient en additionnant deux nombres successifs de la suite pour trouver le suivant.
Par exemple: 0.618 + 1 = 1.618 → 1.618 + 1 = 2.618 ... etc.
Attention, sur la 3ème ligne se sont des valeurs approchées, l'exemple d'addition marche bien, car c'est le moment de la suite où le chiffre 1 intervient et qu'il est donc facile de l'additionner. Pour les autres il faut utiliser la valeur exacte.
Suite de Fibonacci
La suite de Fibonacci a été découverte par Léonardo Fibonacci en étudiant la croissance des générations de lapins.
La suite de Fibonacci est une suite d'entiers dans laquelle chaque terme est la somme des deux termes qui le précèdent. Elle commence généralement par les termes 0 et 1 (parfois 1 et 1) et ses premiers termes sont: 0, 1, 1, 2, 3, 5, 8, 13, 21, etc.
Les quotients de deux termes consécutifs de la suite de Fibonacci sont les meilleures approximations du nombre d'or.
| 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 | 610 | 987 | 1597 | 2584 | 4181 | 6765 | 10946 | 17711 | … |
C'est à partir du quotient de 144/89 que l'approximation atteint la précision qui est couramment utilisée du nombre d'or.
144/89 = 1.617977
Ainsi, dans la nature, un monde fini et concret et pas un monde mathématique parfait, c'est une approximation du nombre d'or qui est utilisée très souvent. La meilleure approximation est la suite de Fibonacci.
(En d'autre mot, par exemple un écran d'ordinateur un a nombre fini de pixel, ainsi un design doit avoir un nombre entier de pixels, il n'est pas possible de faire des fractions de pixels. Donc pour afficher un idéal mathématique, on fait une approximation Dans la nature c'est pareil.)
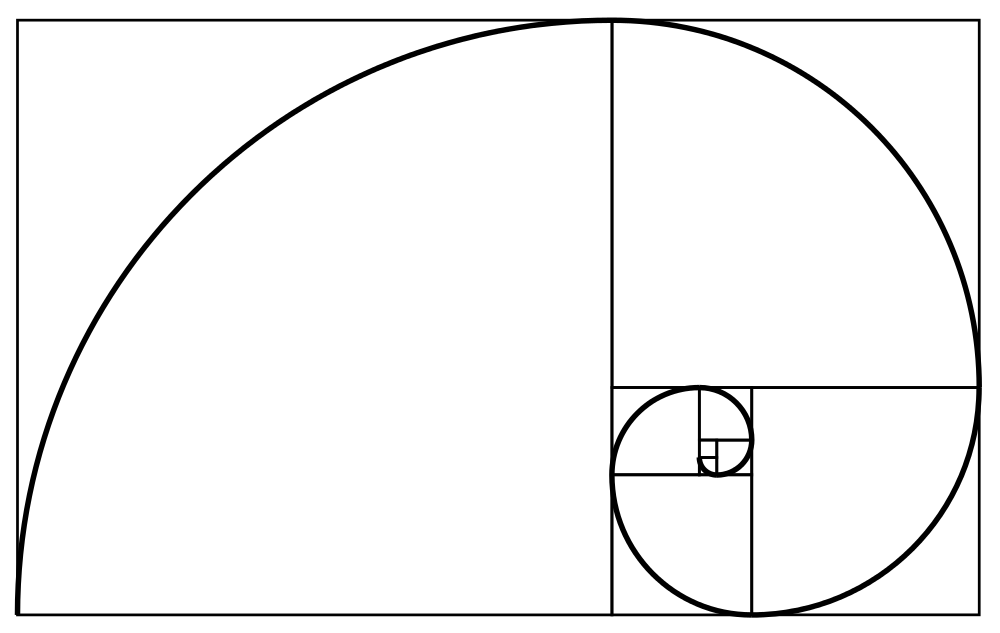
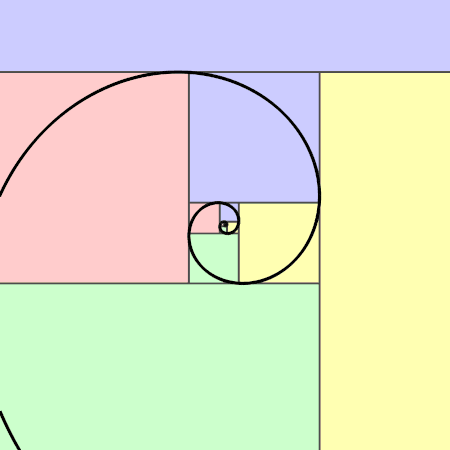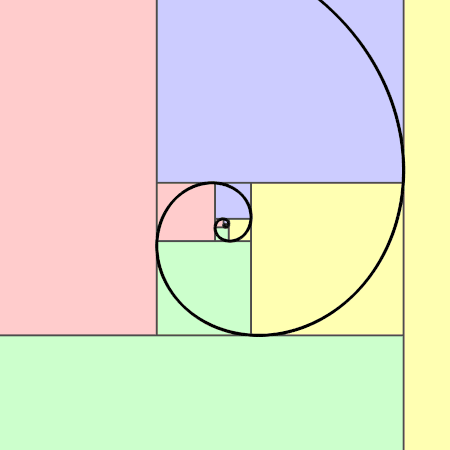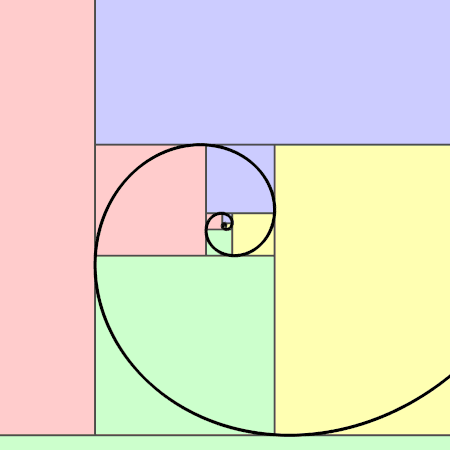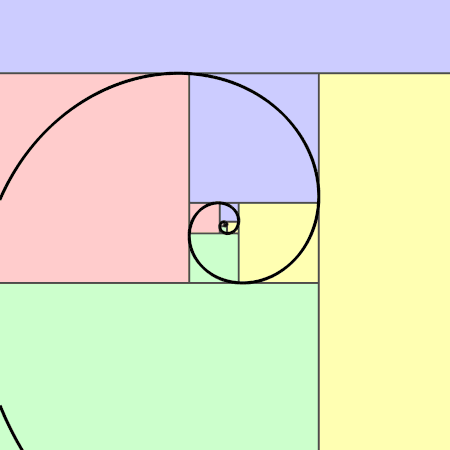
La spirale de Fibonacci
En construisant une structure faite uniquement de lignes droites (Très masculines), il est possible de construire une superbe spirale avec une belle courbe (très féminine).
Il s'agit à la base d'un rectangle d'or qui est découpé en un carré et ..... un autre rectangle d'or ! (On reconnait ici le côté fractal du nombre d'or !)
Il suffit de faire un cercle au compas dans chaque carré. (de la longueur du côté du carré)... et voilà, il y a une superbe spirale qui est ainsi construite.
Ça se semble toujours incroyable qu'on puisse faire des cercles qui correspondent chacun à leur échelle et que pouf... à la jonction ça passe si harmonieusement !! C'est la magie des fractales...
La spirale d'or est très utilisée dans la nature.
Le nombre d'or en phyllotaxie
La nature utilise fréquemment la suite de Fibonacci comme base de construction. (pétale, pomme de pin, etc..)
On parle de phyllotaxie. Il y a plein d'exemples sur cette page.
Il faut se souvenir que le nombre d'or φ est un rapport. Donc au lieu de faire des rapports entre des longueurs des droites comme on l'a fait jusqu'à présent. On va ici faire un rapport sur des bouts de circonférence de cercle.
Donc la circonférence c = a + b
a/b = c/a = φ
(Donc le rapport entre la grande portion de la circonférence et la petite portion de la circonférence qui reste est égale au rapport entre la circonférence complète et la grande partie de la circonférence .. et la seule valeur de rapport possible, c'est φ)
On obtient donc un angle d'or.
Si l'on détermine l'angle en degré qui correspond on arrive à ≈ 137,5° (C'est donc l'angle en rouge)
Les feuilles se positionnent très souvent de cette manière. Tous les 137° une nouvelle feuille pousse...
(Il semble que ça marche avec 80% des plantes. Selon p.74 de: Jean-François Morot-Gaudry, Biologie végétale : Croissance et développement, Dunod, )
 Voici ma vidéo sur le sujet....
Voici ma vidéo sur le sujet....
... et une autre....
Sur cette pomme de pin, on observe qu'il y a un nombre de spirales qui tournent dans un sens (rouge) et un nombre dans l'autre (bleu). Le nombre de spirale dans un sens et dans l'autre est tombe toujours sur une suite de 2 nombres consécutifs de la suite de Fibonacci.
(En 1968 le mathématicien Alfred Brosseau a observé 4290 de pommes de pin et conclu que c'était vrai à 98.2%. Le botaniste Roger V. Jean a refait une telle étude en 1992 avec plus de 12750 pommes de pins de différents genres et il est arrivé à 92% de pives arrangées ainsi. Source: p132 du livre: Le nombre d'or: le langage mathématique de la beauté )
Le nombre d'or en astronomie
Le nombre d'or semble aussi utilisé dans l'agencement des planètes !
En effet, c'est étonnant. Si l'on divise le nombre de jours (terrestres) que la Terre met pour faire sa révolution (sidérale) autour du soleil, par le nombre de jours (terrestres) que Vénus met pour faire sa révolution (sidérale), on obtient comme résultat: le nombre d'or φ (à 99.53%).
Si t'as pas compris la phrase ci-dessus, je fais en bref: le temps que met la terre pour faire un tour autour du soleil / le temps que met vénus pour faire un tour autour du soleil = φ.
J'ai tenté de faire le même calcul avec les autres planètes... mais ça marche pas !
(Mais c'est quand même intéressant. On a une valeur qui est dans une fourchette assez précise. Il semble y avoir une progression régulière. Il y a pourtant un bug, un grand saut dans cette progression entre mars et jupiter. Comme il y a là une ceinture d'astéroïde, je me dis qu'il y avait peut être là une ancienne planète détruite et que si on l'incluait on resterai dans la fourchette que j'ai découverte là.... à creuser... mais pas maintenant)
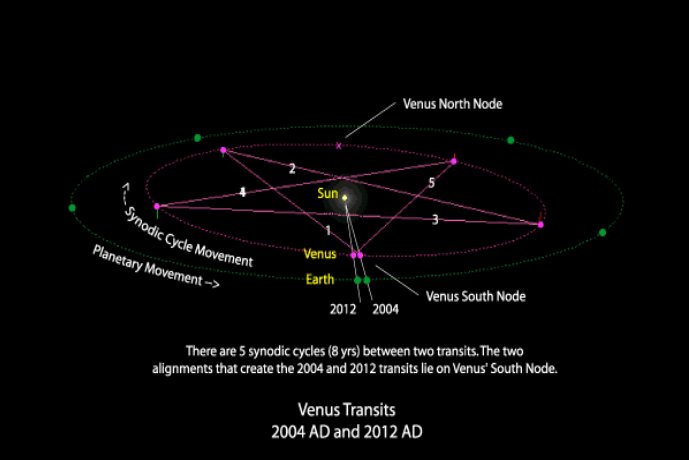
Venus propose facilement des relations avec le nombre d'or, car la conjonction vénus terre soleil vue de la terre forme un une étoile à 5 branches et un pentagone... forme qui contient naturellement le nombre d'or.
De plus le transit de Vénus , événement plus rare, mais également en lien avec la terre, le soleil et vénus, montre aussi un forme d'étoile à 5 branches et inclus donc lui aussi un lien avec le nombre d'or.
Je suis persuadé que l'on trouve encore le nombre d'or dans beaucoup d'endroits en astronomie. Ne serait que les galaxies en spirale ? .. C'est une spirale d'or ? Il y a tout un débat là dessus... je te laisser chercher si ça t'intéresse...
Le mathématicien Jean-Marie Souriau, passionné de géométrie, s'est aussi intéressé aux périodes des orbites des planètes du système solaire. Il a trouvé que les périodes d'orbite des planètes augmentent selon une progression qui se calque très bien sur les valeurs d'une suite de Fibonacci. (en fait, une valeur sur deux !). Ce qui montre là qu'il y a vraiment un lien entre la dynamique du système solaire, l'emplacement des planètes et le nombre d'or.
En fait c'était pas nouveau. L'astronome Kepler l'avait aussi remarqué. Il s'est intéressé au lien entre le nombre d'or et Vénus... et c'est là qu'il est est tombé sur une relation intéressante qu'il a généralisé sous forme de la 3ème lois de Kepler (lois des périodes) qui est largement utilisée de nos jours en astronomie.... et de là Newton en a tiré sa loi sur la gravitation !... Car on voit qu'il y a un lien, un facteur entre une force et une masse planétaire. C'est ainsi que l'on trouve la constante gravitationnelle.
... Là je me dis qu'on jour il faut que je creuse l'histoire, car il y a certainement un lien entre la gravité et le nombre d'or non ?
Je ne suis pas le seul a avoir cette intuition, voici une recherche qui évoque la notion de masse planétaire... et le nombre d'or...
Le nombre d'or dans l'ADN
C'est le Dr ingénieur en mathématique et informatique Jean-Claude Perez qui a découvert la présences du ratio doré sous forme de la suite de fibonacci dans la répartition des bases de notre ADN !
Au début des années 1990, il entend parler du début du séquençage complet du génome humain. Ce chercheur en informatique chez IBM se dit qu'il va donc faire une recherche pour trouver de l'ordre dans le chaos de la masse de données fournie:
"Si je recherchais dans les longues séquences d’ADN déjà disponibles des proportions de nucléotides TCAG qui suivent ces proportions : par exemple, sur 89 bases TCAG contigües, trouve-t ‘on 34 bases T et 55 bases C, A ou G ? 34 55 et 89 sont 3 nombres de Fibonacci dont le rapport approche Phi le Nombre d’or …".
Bingo ! Ça marche. Comme en phyllotaxie, les bases ADN suivent une logique basées sur les nombres de la suite de Fibonacci !
Il en a déduit en 2008 l'équation de la vie:
Proj (m) = [1-[4π√ΦΦΦ²]] m
Avec
√φ = 1/ √ Φ
φ = 1/Φ
φ^2 = 1/Φ^2
Jean-Claude Perez a écrit plusieurs livres dont notamment Codex Biogenesis - les 13 codes de l'ADN.
Voici le résumé du livre codex biogenesis sur le site de l'auteur...
Le nombre d'or dans la bible
Selon une démarche similaire de traitement du signal et de traitement de l'information, le physicien Nouredine Yahya Bey a découvert que Jésus utilise le nombre d'or en relation avec ses miracles, particulièrement dans les récits de résurrection. (Ex: Il faut 3 personnes et attendre 4 jours pour que lazare reviennent à la vie..)
Il semble y avoir une logique liée à une équation issue du nombre d'or pour pratiquer des miracles. On retrouve les nombres de la suite de Fibonacci dans toutes les actions.
C'est à partir de ce constat, que Nouredine Yahya Bey a utilisé ce principe pour faire du traitement du signal dans l'imagerie médicale, notamment en échographie et il a réussi à ainsi reconstituer des parties normalement invisibles aux appareils de mesures !
La précision atteinte va au delà de limites physiques qui étaient établies jusque là, comme le principe d'incertitude d'Heinsenberg. Principe quantique qui interdit de savoir plusieurs information en même temps sur une particule. Ou encore au delà de la limite statistique de Cramér Rao.
Quand le nombre d'or relie des éléments il existe une information supplémentaire qui permet contre toute attente de reconstituer de l'information inaccessible autrement. Carrément dans ce contexte on peut dire de réssusciter de l'information !
Il raconte tout le détail dans son livre: le code caché des miracle de Jésus
Voici un également un compte rendu d'une conférence Nouredine Yahya-Bey.
Le nombre d'or dans l'art
Le nombre d'or est depuis toujours utilisé par les artistes pour structurer leur oeuvres.
La Vénus de Botticelli est souvent montrée en exemple d'une construction basée sur le nombre d'or.
Pour beaucoup d'artistes le nombre d'or représente l'harmonie, l'équilibre. Les proportions les plus esthétiques.
C'est peut être pour cette raison que le format carte de crédit a été calqué sur le rectangle d'or ? (bien que légèrement différent... pourquoi ?)
Les graphistes modernes aiment aussi beaucoup la section dorée, les proportions au nombre d'or.
Voici un article complet avec plein d'exemples sur les propriétés du nombre d'or dans le design, notamment des logos...
Le nombre d'or dans l'architecture
En architecture c'est le Parthénon qui est souvent cité comme ayant son fronton qui est structuré sur le nombre d'or.
Les rangées de gradins du théâtre d'épidaure sont également calquées sur les nombres de la suite de fibonacci.
Les rapports entre les nombres de ces gradins des deux niveaux encadrent le nombre d'or (34/21 = 55/34 = 1,61..)
On ne le dit pas assez, et on verra que c'est fondamental pour la suite de cet article à propos d'une ancienne unité de mesure basée sur le nombre d'or, la grande pyramide de Gizeh, la pyramide dite de Chéops encode le nombre d'or dans ses proportions.
Il y a tellement de liens possible que tout ça mérite un article entier. Mais voici déjà l'essentiel.
- La hauteur de la pyramide vaut √φ fois la demi base. (1/2 longueur d'un côté)
- L'apothème de la pyramide vaut le nombre d'or φ. (La distance du sommet au centre de la base.)
- La chambre haute, dite du Roi, de la pyramide contient une géométrie incroyable faite de nombreuses résonances entre le nombre d'or, et son carré. Ceci tout simplement, car le la coudée royale égyptienne qui est utilisée pour la construction de la pyramide, (mais aussi des cathédrales comme on le verra si dessous) est égale à φ^2 / 5, soit le nombre d'or au carré divisé par 5. (c'est une des manière de déterminer la coudée royale égyptienne.)
Plus récemment, l'architecte Le Corbusier a également créer le Modulor. C'est un outil basé sur le nombre d'or qui fourni les proportions d'un humain standardisé. Cet outil peut être utilisé en architecture pour la création de bâtiments et de mobilier qui est en harmonie avec l'humain.
Le billet de CHF 10.- de la série en train de se faire remplacer a été conçu en l'hommage du Corbusier. On voit son Modulor sur le billet.

Comment construire à base du nombre d'or
Le nombre d'or est souvent utilisé en géométrie sacrée. Voici quelques exemples...
Plus haut on a déjà vu la construction du rectangle d'or.
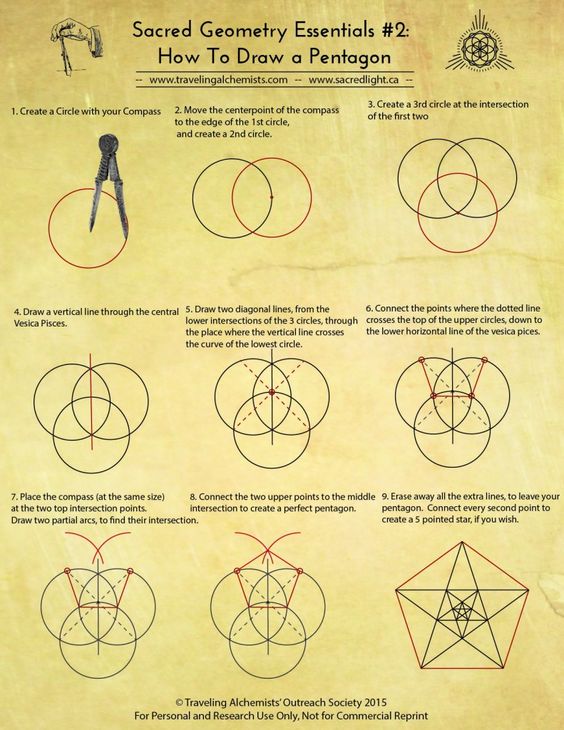
Voici des petits tuto de construction géométrique pour utiliser le nombre d'or φ. Le pentagone contient naturellement en lui tout ce qu'il faut pour avoir le nombre d'or inscrit plusieurs fois sous plusieurs forme.
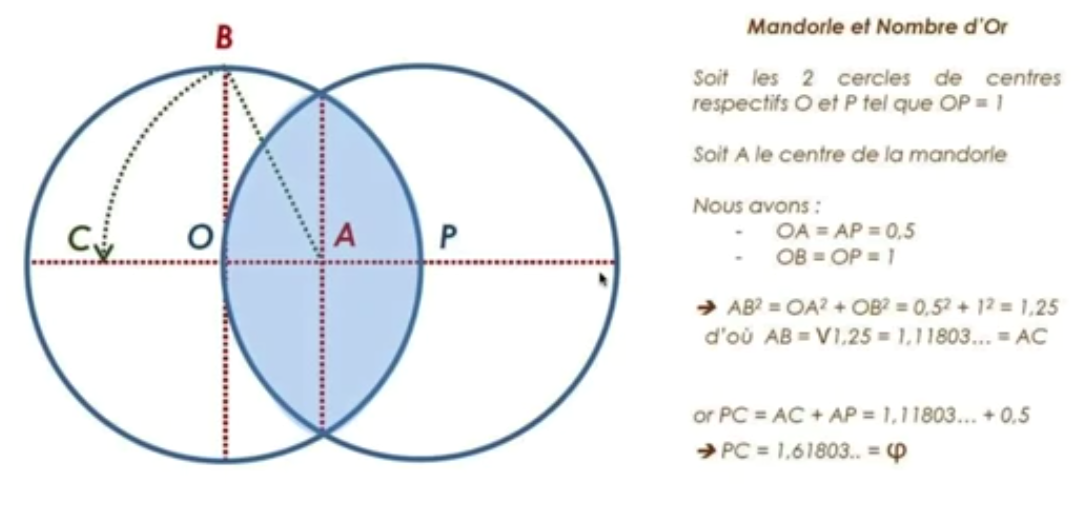
La mandorle est aussi une figure fréquente dans la géométrie sacrée. On peut la construire en la calibrant sur le nombre d'or.
Unité de mesures basées sur le nombre d'or
Il existe plusieurs manières de faire des systèmes de mesures dit "universels".
Le mètre
De nos jours, on utilise majoritairement le système métrique et le système international d'unité qui en découle. On est habitué aux rapports en base 10 entre les différents "niveau" des unités. On a même donnée des noms aux préfixe des unités qui sont des puissance multiple de 3... (ça parait hyper compliqué dit comme ça... mais c'est simple)
Ce sont les fameux: kilo, Méga, Giga.... utilisé pour 1000, million, milliard.... et en symétrie pour ce qui est petit: milli, micro, nano, femto, ato.. mille fois plus petit que 1, un million de fois plus petit... etc.. (donc la nano technologie, c'est ce qui est 1 milliard de fois plus petit que l'unité métrique)
Les rapports sont donc simples, car notre système de numération est en base 10. (et celui de ordinateur en base 2..)
Bon une fois qu'on sait diviser un mètre en millimètre.... ou le multiplier en kilomètre... Il ne reste plus qu'à savoir quelle est la longueur d'un mètre.
Alors on défini le mètre comme étant la 10 millionièmes part du quart du méridien terrestre.
(Donc du quart de la circonférence de la terre qui passe par les pôles. Car dans l'autre sens c'est pas pareil et en fait la définition du méridien a changée depuis !)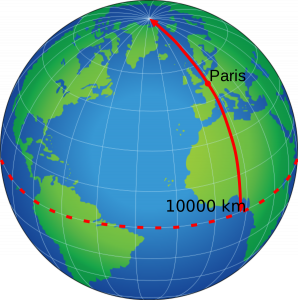
La légende dit que c'est lors de la révolution française que l'on a voulu se débarrasser des unités de mesures anciennes basées sur la longueurs des pieds et des coudes des rois et adopté un étalons de mesure universel donc basé sur la taille de la Terre ce qui ainsi met sur un pied d'égalité tous les habitants de la planète.
Je dis que c'est une légende, car plus je creuse l'histoire, plus je découvre qu'en fait c'est pas tout à fait exact ! En effet, c'est bien lors de la révolution française qu'on a adopté massivement cette unité de mesure et que Napoléon s'est chargé de la diffuser par la force dans toute l'Europe.
Mais plus je me document, je vérifie et je mesure des lieux anciens, plus j'observe que le mètre était déjà largement connu avant la révolution française !
De plus, la mesure de la planète Terre, donc en racine grecque La "géo-métrie" semble se faire depuis des temps très anciens. On se souvient d'Eratosthène qui a mesuré la terre il y a plus de 2000 ans, avec une erreur de 1%.
Et il semble que l'idée d'utiliser la mesure de la Terre comme unité de mesure est très ancienne aussi.
En 1780, Alexis-Jean-Pierre Paucton disait déjà dans son Traité de Métrologie:
"Je prouve que les Anciens avoient un étalon naturel de mesure, pris dans la grandeur d'un degré du méridien, & que dès les temps ses plus reculés, à remonter même avant la fondation de Ninive, de Babylone & des Pyramides d'Egypte, la circonférence de la Terre avoit été mesurée aussi exactement qu'elle l'a été dans ce siécle ; démontre que cet étalon immatriculé dans la nature & de la valeur de la quatre-cent-millieme partie d'un degré du méridien , étoit universel & commun à l'Asie, à l'Afrique & à l'Europe, à quelques exceptions près ; qu'il étoit celui des Perses, des Arabes, des Juifs, des Egyptiens, des Espagnols qui l'ont conservé jusqu'à ce jour presque dans son intégrité, des Gaulois , des Bretons & des Germains ou Allemands, chez qui on le retrouve encore aujourd'hui dans la plupart des Villes les plus considérables ; compare , d'après les rapports donnés par les Ecrivains, cette Mesure universelle aux nôtres & aux autres Mesures particulières de l'Antiquité, qui font les Mesures Romaines, les Mesures Grecques Olympiques, les Mesures Grecques Pythiques & Maríeilloises qui sont encore en uíàge aujourd'hui en plusieurs Villes de la côte de France qui confine à la Méditerranée, & nommément à Marseille, à Gênes & à Montpellier, & enfin les Mesures des Tongres ou des Bataves, qu'on retrouve également dans le Brabant, la Hollande & ailleurs."
A méditer sur l'histoire officielle...
Je recommande pour ça la lecture des livres d'Edmée Jomard qui raconte la campagne en Egypte de Napoléon.:
Il semble bien que les savants français qui accompagnaient Napoléon étaient très très intéressés par les unités de mesures égyptiennes et une légende qui dit qu'il faut chercher vers l'orient "un système métrique fondé sur les bases naturelles".
Ils ont pour ce faire désensablé la grande pyramide de Gizeh pour en prendre les mesures.
"Il est donc naturel de penser que l'étude des monuments laissés par les égyptiens y fera retrouver leur système métrique: c'est là la fin essentielle de notre travail" Edmée Jomard à la p5 du tome 7 de description de l'Egypte.
On peut donc se poser la question de savoir si le mètre actuel, n'est pas la mise au goût du jour d'une ancienne unité de mesure qui existait déjà auparavant ?
... et si ça t'intrigue, fait comme moi, va voir la pierre angulaire qui est dans le sol de la Cathédrale de Fribourg... elle fait bien 1m de diagonale !
... Et bien plus loins dans le passé on trouve le disque de Nebra qui fait 1m de circonférence et Stonehenge qui fait 100m de circonférence....
Bon.. ici n'est pas l'objet de mon article, donc on va revenir au nombre d'or, et je ferai un prochain article sur l'histoire du mètre.
Donc si l'on est habitué au système décimal pour réalisé une division des échelles de l'unité de mesure. On peut aussi faire autrement.
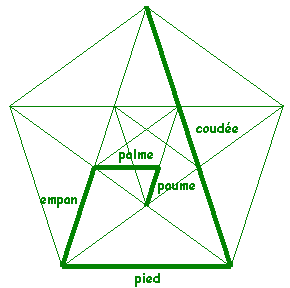
La canne des bâtisseurs de cathédrale
Les bâtisseurs de cathédrale utilisaient un système basé sur le nombre d'or pour définir les unités de longueurs de base:
- La paume → 34 lignes
- La palme → 55 lignes
- L'empan → 89 lignes
- Le pied → 144 lignes
- La coudée → 233 lignes
Voici une canne des bâtisseurs pour mémoriser la longueur de ces unités de longueurs.
Ces différent noms correspondent aux rapports de longueur entre différentes partie d'une étoile à 5 branches inscrite dans un pentagone.
Comme on l'a vu plus haut, cette géométrie contient intrinsèquement le nombre d'or à de multiples endroits. On peut aisément observe aussi le changement d'échelle fractal qui est possible avec l'étoile à l'intérieur de l'étoile.... (mais inversée...)
Une bonne approximation pour réaliser une canne des bâtisseurs, est d'utiliser la suite de Fibonacci. Ainsi à chacune des unités de mesure correspond un nombre de la suite de Fibonnacci. Ce nombre peut représenter des lignes.
Ainsi on arrive à faire correspondre des rapports idéaux basées sur le nombre d'or, et les réaliser concrètement grâce à une addition d'une unité des base qui est la ligne. Mais il faut se rendre compte que la suite de Fibonacci est une approximation. On trouve beaucoup d'incompréhension chez les gens qui cherchent à calculer ces unités de la façon moderne sans avoir compris l'idée des rapports du nombre d'or.
(Ils cherchent à arriver aux rapport en faisant des additions de lignes basées sur le grain d'orge sensé faire 4 lignes)
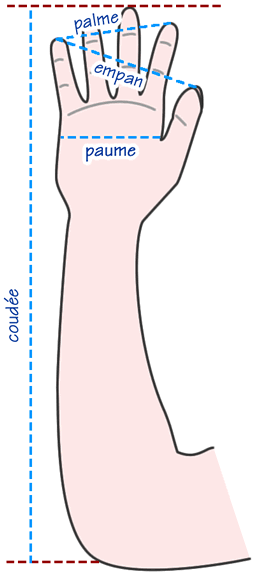
Pourquoi est-ce que ces rapports de longueur portent des noms de partie du corps ?
Il est vrai que c'est pratique dans la vie de tous les jours de mesurer un pied ou une coudée. On l'a toujours sur soi. Ça évite d'être coincé car on a oublié son double mètre !
Personnellement, je m'étonne de voir que, hormis le pieds qui est sur une autre partie du corps, le système de longueurs colle passablement bien avec les rapports de proportion.
Quand on voit ci-dessus que le nombre d'or est présent partout dans la nature. Est-ce que finalement le corps humain ne serait-il pas lui même basée sur le nombre d'or ?
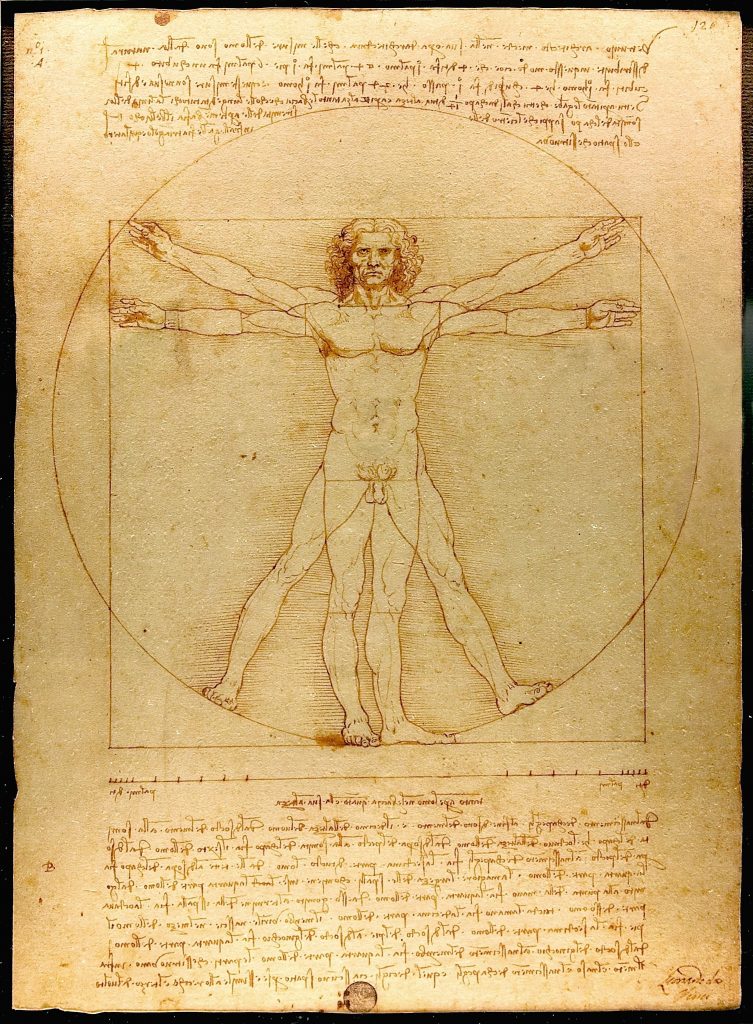
C'est aussi l'avis exprimé par Léonard de Vinci avec l'homme de Vitruve, qui exprime l'hommme aux proportions parfaite qui s'inscrit parfaitement dans les mesures de l'univers. (inscrit dans un carré et un cercle, souvent symbole de la terre et de l'univers.)
C'est aussi ce que l'architecte Le Corbusier avait exprimé avec son Modulor. (Qui est indiqué en hommage sur les ancien billet de 10 francs Suisse)
Il y a tout un débat sur ce sujet.
Je pense qu'il est temps de se questionner sur la légende de la création du mètre pour remplacer des unités de mesures "arbitraire" basées sur les mesures du roi ?
Est-ce que finalement l'origine de ce système ne serait pas beaucoup plus élégant et pas juste calqué sur taille du pied ou du coude du roi ?
Peut être que c'est une dérive à la longue d'individus assoiffé de pouvoir qui ont imposé leur membres comme référence, sans avoir compris le système mathématique et à la mesure de l'Homme en général qui sous-tend ce système ? On parle de la mesure du corps humain de façon statistique.
Je me questionne passablement là dessus ces temps, sans avoir réussi à vraiment prendre le temps de faire des recherches plus poussées. Il y a plein d'études statistiques qu'il serait bon de faire.
J'ai notamment aussi entendu parler de la taille moyenne d'un enfant à la naissance qui est "par hasard" très proche de la taille de la Coudée Royale égyptienne, soit 52,36 cm ! (Il y a un lien entre la coudée royales égyptienne, le mètre et le nombre d'or... j'y reviendrai !)
Et le poids de l'enfant à la naissance qui approche le nombre π en kg ! Soit environ 3.14 kg.
Bon, alors maintenant on a une manière de subdiviser une unité de mesure, mais ça ne nous donne toujours pas l'échelle utilisée.
Que vaut une coudée ?
Il y a une manière simple de faire. C'est de prendre le Roi, de mesurer la longueur de son coude et de calibrer ainsi tout le système sur cette longueur. On peut ainsi se souvenir qu'une Coudée fait 233 lignes et ainsi redéfinir toute les unités de mesure intermédiaire avec leurs correspondance en lignes selon l'approximation de la suite de Fibonacci.
Ça explique peut être pourquoi il y a des coudées locales, et il y a la Coudée Royale.
Mais avec cette technique on voit que le Roi était un peu difforme.... sauf pour la coudée !
Mais on peut aussi baser l'échelle sur un lien entre le corps humain et la taille de la planète !
L'empan
La première fois que j'ai entendu parler de l'empan, c'était quand j'étais ado. Mon grand père m'avait offert les oeuvres de Rablais. J'y ai vu un livre avec un langage aux tournures de phrase très anciennes et aux innombrables notes de bas de page pour expliquer tout le contexte.
Il y avait l'empan comme unité de mesure. J'y ai appris en note de bas de page qu'un empan vaut 20 cm. J'ai trouvé ça très pratique. Depuis j'utilise régulièrement l'empan comme unité de mesure quand je n'ai pas sur moi mon double mètre !
Et là j'ai rapidement remarqué que 5 empan = 1 mètre.
Donc pour calibrer mon système de coudées, etc... pourquoi ne pas dire qu'un empan, soit 89 lignes = 1/5 de mètre ? Le mètre étant le 10 millionième du quart du méridien terrestre (circonférence)
Et voilà !
=> Là j'entend tout de suite ceux qui me disent.... "C'est pas possible... car le mètre a été inventé à la révolution française !"
Voilà voilà.... c'est pour ça que j'aimerai creuser cette légende.... Car il y a un faisceaux de faits qui montrent que cette fable ne colle pas. qu'il y avait une connaissance plus ancienne du mètre. Ou du mois, d'une unité de mesure qui a un lien avec la circonférence de la terre et qui fait que "par hasard" on retombe sur la même chose !
Alexis-Jean-Pierre Paucton nous dit bien en 1780 qu'il existe une unité de mesure qui vaut "la valeur de la quatre-cent-millieme partie d'un degré du méridien". (Il ne dit pas le nom de cette unité !!)
A la page 110, de son Traité de Métrologie, il dit qu'il utilise la grande pyramide de Gizeh comme élément de comparaison pour retrouver les valeurs des unités historique. (Il n'y a pas beaucoup de monument mesurés précisément tout au fil de l'histoire de l'humanité qui existe encore !)
Paucton nous dit que selon Héron d'Alexandrie (Je crois bien que c'est celui-là de Héron !), 1° du méridien terrestre vaut: "16 2/3 Schenes, 66 2/3 milliaires Egyptiens & Phéniciens, 500 stades, 200000 coudées, 300000 pies philétériens, 360000 pieds Romains, 400000 pieds géométriques, & 533245 1/3 spithames."
Je m'étonne de voir autant de valeurs rondes. (même les 2/3 sont "ronds": ex: 16 2/3 => c'est 50/3)
C'est pour "arrondir" et donc montre une imprécision, ou alors justement ça montre bien que le ° de méridien est une unité fondamentale sur laquelle on a construit d'autres unités de mesure ?
Puis il nous dit que "le côté de la base de la grande pyramide d'Egypte pris cinq cents fois (...)" "(...) chacun en particulier est précisément la même mesure d'un degré".
"D'où je conclus que le côté de la base de la grande pyramide étoit d'un stade juste tel qu'il est défini par Marin de Tyr, par Ptolémée & par Héron."
Un degré de méridien vaut 500 stades, soit 500 fois le côté de la base de la grande pyramide de Gizeh.
→ le côté de la base de la grande pyramide vaut 1 stade
→ un degré de méridien vaut 500 fois le côté de la grande pyramide.
(On aurait donc construit la grande pyramide sur la base de ce coté qui vaut 1/500 de 1° de méridien ?)
Si on reprend ce qu'il disait au début du livre, alors il doit exister une unité de mesure ancienne qui vaut la 1/400 000 d'un degré de méridien.
→1/400 000 de 500 fois le côté de la grande pyramide. (440 Coudée Royales Egyptienne soit ~230m)
Donc d'après les ~230m, je trouve que cette fameuse unité ancienne vaut 28.75 cm.
→ C'est dans l'ordre de grandeur de ce qui correspond à un pied. (mais c'est pas le pieds des bâtisseurs qui vaut plutôt ~32.3 cm)
Donc sachant qu'un pied, c'est 144 lignes. Je peux calibrer le reste de mon système de mesure.
Ceci à partir d'un écrit de ~2000 ans repris dans un écrit d'il y a ~200 ans....
A creuser.....
Les travaux sont en cours.... Je découvre mille choses... Paucton n'est pas allé en égypte, mais Jomard y est allé, et il a mesuré la pyramide.
Il dit dans son Mémoire sur le système métrique des anciens égyptiens... :
"Mais le périmètre de la grande pyramide de Memphis avoit 30 secondes du degré propre à l'Egypte, autrement cinq stades compris chacun 600 fois dans ce même degré: l'apothème avoit un stade; le côté, 500".
Là, ça marche très bien. La longueur du degré du méridien propre à l'égypte (30° de latitude) mesure 110852.4248 m. Si on divise cette longueur par 120 on obtient 923.8m pour le périmètre de la pyramide, soit 230.942 m pour un côté. Ce qui à une coudée près correspond aux 440 coudées officiellement admises. (mais avec de grandes variations suivants les auteurs !) La différence s'explique probablement à savoir si l'on prend en compte le socle de la pyramide où non !
... affaire à suivre quand j'aurai fini mes recherches.... (Il y a vraiment de la matière... et c'est juste incroyable ! ... faut relire les premiers égyptologues, J'ai l'impression qu'ils en savaient plus que ceux de maintenant !)
La Coudée Royale Egyptienne
Vu qu'on parlais de coudée, voici un des plus célèbre. Ça nous permettra aussi d'en savoir un peu plus sur le calcul fait ci-dessus en utilisant une taille de pyramide en coudées.
Alors la Coudée Royale Egyptienne vaut entre 52 cm et 54 cm selon ce que l'on peut lire sur wikipedia. C'est la version officielle, basée sur les différents "bout de bois" qui représentent la coudée qui ont été retrouvé.
Les unités de mesure ne sont pas pour moi quelques chose totalement dénué de sens, qui sortent de nulle part. Elles sont souvent très réfléchie. Il y a un sens derrière une unité. C'est un symbole. Ici, c'est une explication mathématique qui a nous permettre de retrouver la définition de la Coudée Royale Egyptienne.
Comme dit plus haut, j'aime bien voir les maths de manière géométrique.
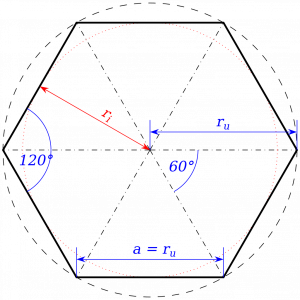
Nous allons ici construire une joli hexagone bien régulier. Depuis que je suis gosse j'aime bien faire ça. C'est surtout depuis que j'ai découvert que c'est tout simple, avec juste un compas.
Il suffit de faire un cercle. De garder le même écartement. (donc le rayon du cercle) et de dessiner des portions d'arc avec le même écartement.
Là on remarque une particularité mathématique, ça me donne exactement 6 parts égales si je coupe ma circonférence avec des tranches de la taille du rayon !
Tout simple de faire un hexagone. Mais quelle lien avec la coudée Royale Egyptienne ?
Et bien le lien est simple. Le fameux écartement de compas que j'ai utilisé pour faire mon hexagone me donne 2 choses:
- L'écartement lui-même, soit une droite entre 2 points. C'est la longueur d'un côté de l'hexagone. (en plus d'être le rayon du cercle)
- Une portion de circonférence du cercle. Soit 1/6 du cercle.
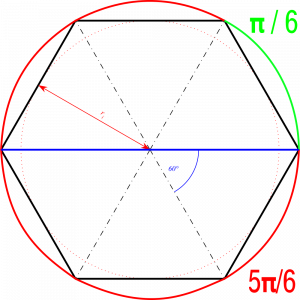
Et voilà.... la Coudée Royale Egyptienne, c'est cette portion d'arc. Ce sixième de la circonférence d'un cercle.
Comment on calcule la circonférence d'un cercle ?
C = 2 π * le rayon = le diamètre du cercle * π
Donc la Coudée Royale Egyptienne, c'est π/6 fois le diamètre. C'est la partie représentée ici en vert.
Ok, bon... En math géométrique abstraite, on voit bien ce que c'est. Mais pour les gens qui aiment les math avec des chiffres... ça fait quoi π/6 ?=> 0.52359877559....
Ok, mais, 0.523 quoi ?
C'est o.523 fois le diamètre du cercle !! On a un juste un rapport. C'est vrai que c'est pas simple de mesurer quelque chose comme ça. Il faut un lien avec la réalité.
Et si je prenais 1 mètre comme diamètre ? ça me donne donc tout de suite une valeur pour la Coudée Royales Egyptienne en mètre.
Donc la Coudée Royale Egyptienne vaut 0.52359877.... mètre !
→ On est bien dans les mesures des bâtons retrouvé qui font entre 52 et 54 cm !
Voilà, c'est très bien. On a retrouvé la valeur théorique de la Coudée Royales égyptienne.
.... mais comme plus haut, j'entends déjà les cris...... mais c'est pas possible... t'as pas le droit de faire ça.... T'es en train de me dire que tu calibres la coudées royale égyptienne sur le mètre !! ... donc un truc qui a été utilisées il y a des milliers d'années par une unité inventée il y a 200 ans lors de la révolution française. C'est pas possible !
Ouais, en effet, ça pose un soucis ! C'est pour ça que cette explication n'est pas officiellement admise par l'archéologie, que la page wikipedia n'en parle pas. (Mais il y a un débat sur la page de discussion)
Mais alors pourquoi ça marche ? Certains vous dirons que c'est Dieu.... et d'autres le hasard... (ce qui est assez proche... évoquer le hasard pour tout ce que l'on comprend pas ça ressemble à une religion... alors qu'il est si simple de dire: "Je ne sais pas". )
Comme dit plus haut. Je ferai bientôt un article là dessus, car il commence à y avoir beaucoup de coïncidences. Le hasard fait vraiment bien les choses, il place le mètre dans bon nombre d'objets, surtout dans des cathédrales et observatoire astronomique anciens.
Selon le même principe, le pied druidique c'est 1/10 de la circonférence d'un cercle de 1m de diamètre. → soit π/10 en mètre..... Donc il y a plein d'unités liées au mètre.
One more thing...
Ce n'est pas tout... On est bien ici en train de parler d'unité de mesure basée sur le nombre d'or ! Et bien il se trouve que la Coudée Royale Egyptienne a aussi un lien avec le fameux nombre φ.
On a vu plus haut que la Coudée Royale c'est le bout vert du cercle, soit π/6. Le reste du cercle, le bout en rouge, vaut donc 5 * π/6.
En nombre ça donne:
5 π/6 ≈ 2.61799387799
Ça te rappelle pas quelques chose écrit tout en haut ?
φ² = φ + 1 ≈ 2.6180339887
En effet, à un cheveu près, c'est pas "exact" ce qui génère de grand débat, la partie rouge du cercle vaut φ².
Si c'est la précision mathématique que l'on cherche, c'est pas parfait. Mais si c'est pour une construction. La différence est minime, quand je dis à un cheveu près.... c'est déjà très gros un cheveu. Là on est à un centième de mm d'écart si l'on se base sur le cercle de 1m !
Liens mathématiques entre le nombre d'or et des nombres "spéciaux"
Cette petite in-exactitude me questionne beaucoup et elle fait aussi couler beaucoup d'encre (ou de pixels) chez les sceptiques.
Il faut quand même dire que l'on mélange là des nombres très spéciaux. Les nombre φ et π sont irrationnels. Il ne se mélangent pas facilement à d'autres. Pire, π est transcendant. Donc réussir à faire quelques chose qui mélange ces deux nombres, c'est peut être juste pas possible ?
Sur un plan philosophique le nombre d'or est souvent vu comme la perfection a atteindre, et les constructions qui en découlent sont généralement réalisées avec une approximation à l'aide de la suite de Fibonacci, car c'est le moyen accessible dans l'imperfection du monde.
Ainsi la coudée royale égyptienne est peut être la meilleure approximation possible du lien enter le π et φ ?
Le problème de la quadrature du cercle est un problème de mathématique qui a occupé les mathématiciens pendant des millénaire. Il s'agit de construire avec les outils du géomètre, un carré de même air, qu'un cercle donné. Pour faire un carré, on a besoin de sa diagonale, et il se trouve que cette diagonale comme je l'ai mentionné plus haut, c'est la racine carrée. Et là il faut trouver la racine carré de π.
Comme π est un nombre transcendantal, et bien il est impossible de réaliser cette opération par une construction géométrique, juste avec un compas et une équerre.
J'ai cherché si il y des liens connus entre ces deux nombres spéciaux. J'ai trouvé un document qui mentionne une solution approximative à 1% près et une à 0.02% près en passant par le nombre i , soit l'unité imaginaire des nombres complexes. Il est intéressant que cette solution fasse intervenir le nombre e ! un autre nombre étrange !
φ² + e² + (i/e)² = π²
Donc effectivement, la Coudée Royale Egyptienne semble vraiment la meilleure approximation de ce lien entre π et φ .
Conclusions
J'ai ouvert beaucoup de portes dans cet article. Le nombre d'or fascine depuis des millénaires, et je crois que ce n'est pas fini.
Je pense qu'il y encore beaucoup à redécouvrir à propos de la compréhension des anciens à propos de ce nombre, de ce rapport que l'on trouve partout dans la nature, et qui semble une référence universelle. Donc c'est bien compréhensible qu'on ai voulu l'utiliser comme base d'unités de mesure.
J'ai l'intuition, qu'il y a encore quelque chose à découvrir autour du mètre. Est-ce que cette unité est naturelle ? Elle est calibrée par rapport à la planète, mais est-ce qu'il y a quelques chose de plus ? Tout comme on a vu qu'il y a un lien fractal entre les triangles dans une étoile à 5 branches. Il y a peut être un lien fractal entre la dimension de la terre et la dimension humaine et de là découlent des unités de mesure naturelle à échelle humaine, comme à échelle planétaire, voir universelles.... ?
C'est en tout cas suggéré par Leonard de Vinci dans son homme de Vitruve...
A méditer.



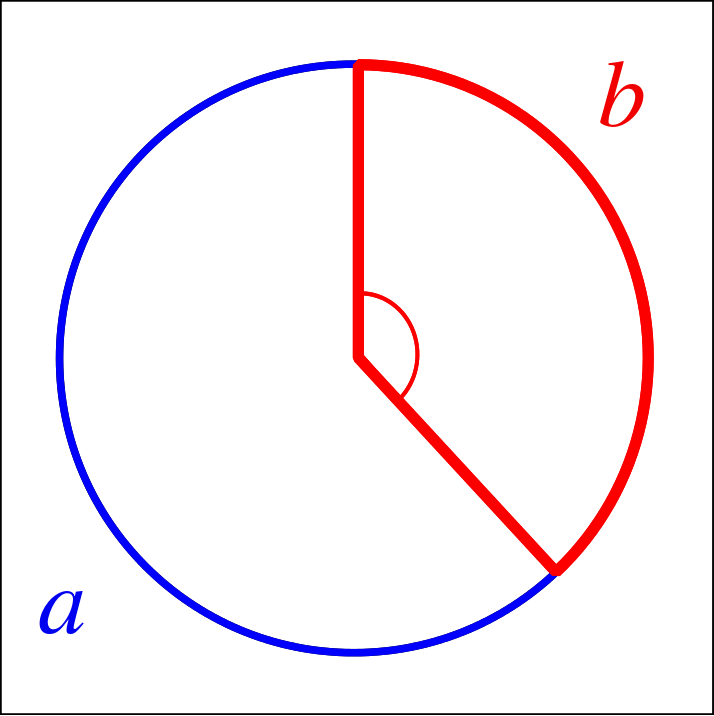






[…] nombre d’or est un nombre particulier qui est le rapport entre la partie et le tout, ceci à plusieurs […]
[…] est vrai qu’il y a de nombreux thèmes qui sont semblables et repris. (notamment la notion de lien entre la coudée royale égyptienne et le mètre, les constructions cyclopéennes de part le monde qui sont énormes, vieilles et anti-syssmiques, […]
[…] Connaissance – Lunaire – Polarisé – Phi (5/6ème de cercle) – […]
[…] pas n’importe quelles mathématiques, celles du nombre d’or, celle de la géométrie […]
[…] le solstice d’hiver et l’équinoxe de printemps qui correspond à la section dorée, le nombre d’or. Tout comme la fête de l’Assomption est placée sur en proportion dorée entre le solstice […]
je doit faire un exposé sur la résonance et conscience et j’en ne trouve pas le liens du nombre d’or et de la résonance et conscience
Bonjour,
Je ne suis pas certain de comprendre l’idée ?
Mais on peut voir dans le nombre d’or une résonance. C’est pas si simple à expliquer… mais ça se voit au début de l’article sur le schéma qui montre la section dorée.
« Le nombre d’or est le seul rapport qui met en résonance la partie avec le tout. On peut donc le voir comme étant une résonance (fractale) entre la créature et son créateur. »
Si on prend une droite, c’est le tout. Puis on la coupe en 2… mais pas n’importe où … à la section dorée. Soit à cet endroit particulier ou on arrive à faire que le rapport de longueur entre ces deux nouvelle partie soit identique au rapport entre la grande partie coupée et le tout.
… mais comme le tout englobe aussi la petite partie… c’est un truc circulaire… on a une boucle de rétroaction.
La petite partie influence aussi sur le rapport entre la grande et le tout…
On est donc la dans une notion de rapport fractal. On peut couper à l’infini.. (voir la spirale dorée.)
Ainsi on a là une résonance à plusieurs échelles.
La chambre haute de la grande pyramide de gizeh est construite avec de nombreux lien en rapport avec le nombre d’or…
[…] En étudiant les dimensions, c’est normal ! Tout est en résonance, on retrouve les rapports musicaux de la gamme de ptolémée dans les rapports entre les murs. On retrouve également une géométrie basées sur un double carré qui ouvre sur toutes les combinaisons possibles avec le nombre d’or. […]
Vorrei segnalarvi che l’Angle d’Or non solo descrive la fillotassi delle piante ma contiene un’informazione riguardo all’altro angolo 𝛑; infatti il regno dei Numeri ama custodire le costanti cosmiche che devono essere svelate tramite altre costanti.
Considerate l’angolo ed il suo Log ed abbiamo;
log (180°- 360°/𝛗^2) = log (180°-137°,507764) = log 42°,492236 = 1,628309585..
che significa [ 1+ 2( 0,3141 547924….)=1,628309585 e risolvendo rispetto a Pi si ha
(1,628309585-1): (10/2)= (0,628309585)*5 = 𝛑 =3,141 547 9585…
e qui occorre dire che si tratta del valore dell’angolo Pi e non un rapporto fra circonferenza e raggio; insomma ,la Natura ci dice che 𝛑 governa, insieme a 𝛗 sia il mondo finito delle cose sia l’infinito della spirale cosmica.
Torino li, 19/7/2019 ( mail- giuseppelucianof@gmail.com)
Passionnant tes articles!!! J’aime ta folie 😉 tu donnes bcp de pistes pour aller lus loin ce que j’apprécie énormément. Merci!!!
Youhouhou…
Plus on est de fous, plus il y a de riz !!
Les fous ouvrent les voies que les sages empruntent par la suite….
Merci pour ce commentaire très encourageant ! 🙂
Oui, c’est un domaine avec énormément de matière pour aller plus loin.
Donc.. parfois je vais plus loin…. et justement je viens de publier un article à propos de la géométrie sacrée. Il est tout à fait complémentaire à cet article-ci.
Bonne lecture… et à la prochaine !
https://martouf.ch/2019/11/quest-ce-que-la-geometrie-sacree-introduction/
Il y a une relation entre le mètre, la coudée, pi et phi car le diamètre de la Terre est par pur hasard égale à racine de phi fois 10 millions 🙂
a salinas,
Nulla nel Cosmos è per caso!
una prova?
distanza Terra-Luna; d=2^10 x 5^3 x 3=384.000 (km)
la Legge del Numero Pitagorico governa l’ordine del Sistema solare,
Mi prendo la libertà di segnalare, riguardo al Phi ,che esso è generato sia dai Numeri sia dalle forme della geometria ,che significa immaginare una posizione spaziale del numero.
Ed ecco cosa ho scoperto: immaginate di tracciare un cerchio di diametro 5( Numero sacro per Pitagora),poi risolvere l’equazione aX^2 – bX +c = 0
le cui radici sono 4 ed 1 ; poi dal punto di coordinate X=4 innalzate un segmento che interseca la circonferenza nel punto P; poi unite con due segmenti P alle estremità del diametro.Ottenete un bellissimo triangolo ,con angolo retto opposto, al diametro -ipotenusa.( e questo fatto era già implicito nell’equazione uguagliata a zero ,dove lo zero implica(significa ) che esso è il coseno di 90°;
tale altezza è; h=2
Ora direte: ed ora? sommate l’ipotenusa al lato minore e dividetelo per il cateto maggiore ed ottenete ; 𝛗 =(5+√5) / (2√5)= 1,618033989..per l’inverso invece sottraete all’ipotenusa il cateto minore e dividete per il cateto maggiore;
1/𝛗 = ( 5 – √5)/ ( 2√ 5 )= 0,618033989..
Se poi inserite nel grafico o cartesiano la parabola (X^2-5X+4 ) scoprirete che la parabola è collocata nel primo quadrante insieme al cerchio ; vi rimane solo da calcolare il vertice della parabola di coordinate (2,5;-2,25).
In buona sostanza un tripudio di matematica: algebra con il teorema di Viéte-geometria euclidea, con Pitagora ed Euclide e geometria analitica con Descartes : Insomma un bijou di prova di verifica per le medie superiori al terzo anno.
Saluti da Joseph( Torino/Italia)
li, 24 settembre 2019
(giuseppelucianof@gmail.com)
[…] est la même que la coudée utilisée par les bâtisseurs de cathédrale dans le système de « quine des bâtisseurs » (aussi appelé parfois « pige des bâtisseurs » et qui sert à construire des outils comme […]
Il y a une relation entre le mètre, la coudée, pi et phi car le diamètre de la Terre est par pur hasard égale à racine de phi fois 10 millions 🙂
Merci pour ce commentaire tout à fait pertinent !
Un jour je ferai un article pour décrire ceci…. ça pourrait être la suite de mon introduction à la géométrie sacrée…
https://martouf.ch/2019/11/quest-ce-que-la-geometrie-sacree-introduction/
Là j’y décrit que √φ ≈ 4/π …..
C’est la hauteur de la grande pyramide de Gizeh.
.. et en effet, on retrouve là aussi les mêmes proportion que la Terre…. à un facteur d’échelle près. (le 10 000 0000ème)
Par contre perso, j’arrive pas à savoir si la valeur juste c’est √φ …. ou si c’est 4/π ?
Le raisonnement que je présente dans mon article sur la géométrie sacrée, c’est que 4/π est la valeur juste. Mais que π est un nombre non constructible, donc on va utiliser sa meilleure approximation constructible, soit √φ.
Je trouve ça plausible… mais la question reste ouverte. Vous en pensez quoi ?
la relazione fra 𝛗 et 𝛑 è mediata dal rapporto fra l’ipotenusa del triangolo retto pitagorico ed il suo cateto più lungo; infatti 5/4=1,2
𝛗^2 *5/4= 2,61803399 * 1,2 = 𝛑 = 3,14164 0787….,che per quei tempi era considerato certamente un numero sacro ,da non profanare e tenerlo segreto alla curiosità degli acustici.
Mi devo correggere riguardo al rapporto 5/4 che non offre 1,2 che è il rapporto fra 2*3/5 ; dunque si tratta del rapporto fra il cateto minore e l’ipotenusa del triangolo retto di Pitagora( ovvero 2(a/c)= 2(3/5);
Vi domandavate da dove arriva la CRE = 0,5236..?
Ecco la formula; [1+1/𝛗^2]^(-1)-(1/5)=( 0,7236..- 0,2)= 0,5236..( C.R.E.)
Infine, nel suo articolo ,molto ampio Lei fa riferimento al tempo di rivoluzione della Terra intorno al Sole che Keplero ha(avrebbe )calcolato correttamente. T= 365,24..
Lei conosce la formula? ( su Wikipedia viene indicata una formula con un coefficiente K che però non viene calcolato(sarà segreto?) a mio avviso il decimale è sottostimato perché non rappresenta il 1/4 (circa 6 ore) che nel quadriennio implica 1 giorno(24) da aggiungere al 365 gg. ( mese di febbraio di 29 gg.)
Keplero , come Pitagora avrebbero scritto 365,528536658..
Se le interessa le offro la possibilità di interpretare la formula che si deriva, con una buona dose d’intuizione, dalla relazione di Pitagora (a,b,c).
cordialità.
li, 14 dicembre 2019
= errata corrige=
(a c u s m a t i c i ) e non acustici .
Merci j’apprends la définition du mot « acusmatique » => https://fr.wiktionary.org/wiki/acousmatique
[…] de toutes les planètes.Je trouve que c’est très harmonieux !!Il y a certainement une géométrie liée au nombre d’or… ou a son approximation, la suite de fibonacci…. comme l’avait montré Souriau […]
[…] haute de la grande pyramide de Gizeh en granite avec ses proportion parfaitement alignée sur le nombre d’or qui sont des rapports de la gamme musicale naturelle. Personnellement je me suis amusé à moduler […]
Le mètre tel qu’il a été défini il y a deux siècles (avec une erreur sur la taille du méridien, mais bon…) est effectivement de l’ordre d’une double corde de la coudée royale égyptienne vu comme le sixième du périmètre d’un cercle de diamètre de l’ordre du mètre. On sait également que le pendule d’un peu moins d’un mètre bâts la seconde… Mais de là à imaginer que le mètre actuel est exactement associé à la coudée royale égyptienne donnée comme 0,5236 me semble aller vite en besogne même si au néolithique on a pu faire des progrès d’astronomie, et de numération comme d’arithmétique (au moins vous ne faites pas référence à un savoir venu d’extraterrestres et vous restez malgré tout prudent avec un mètre qui serait issu de la nuit des temps, d’autant que vous faites bien part de différentes exactitude, celle d’arpenteurs, de bâtisseurs ou celle de mathématiciens ou logisticiens si on s’en réfère au grecs). On ne sait pas si le nombre d’or (en tant que divine proportion) était connu dans l’Antiquité – ce qui ne veut pas dire qu’il ne l’était pas car il a pu en effet être un secret jalousement gardé vu déjà plus tard les sectes pythagoriciennes – et pour pi le problème est que si la figure géométrique d’un cercle faisait bien partie du paysage culturel géométrique, donner une valeur précise à pi relevait d’un défi assez complexe à relever avec une arithmétique très élémentaire. 3 est grandement suffisant pour plein de choses mais effectivement cela peut poser problème en architecture si on y fait référence de façon fondamentale. On donne aussi souvent la valeur 256/81 à peine plus grande que 79/25 = 316/100. On connait aussi le fameux 22/7 connue d’Archimède, valeur par excès. La valeur 355/226 par excès n’a été donnée qu’au Vième siècle par le mathématicien chinois Zu Chongzhi. Donc penser que pi et phi ont été conçus comme on le conçoit aujourd’hui (transcendant pour pi et algébrique irrationnel pour phi) me semble quelque peu erroné. Je pense que dans l’Antiquité l’idée de nombre était rationnelle (avant Euclide… pour ne pas énerver et on n’est pas à quelques siècles près) et que de surcroît il valait mieux en rester à des numérateurs et dénominateurs (pour parler le langage d’aujourd’hui) pas trop grands et effectivement la suite de Fibonacci nous donne une approche des ratios approchant le nombre d’or. Vous donnez d’ailleurs la valeur 144/89 voire 233/144 comme approximation assez correcte de phi, mais qu’est-ce qu’une approximation assez correcte ? Il faudrait pour cela vous penchez sur les approximations diophantiennes, mais sans aller jusque là avec phi on a phi^2 = phi+1 et 1/phi = phi – 1 qui permettent de mieux juger d’une bonne approximation. Pour moi je trouve que 377/233 commence à être mieux (phi+1 = 610/233) et je vous laisse faire le calcul sur une calculette éventuellement scientifique. Je ne dis pas ça pour vous être désagréable mais parce que 377 et 233 pour les civilisations fondées sur une représentation décimale des entiers accrochent le regard aussi (comme 256 quand on bosse en base 2). La suite de Fibonacci c’est du récent, et si on se plonge dans le passé les fractions que l’on peut tirer de cette suite apparaissent comme les convergents de la représentation en fraction continue du nombre d’or. Sur un plan théorique la notion de fraction continue fait hérisser le poil du commun des mortels, mais sur le plan pratique qu’en est-il du nombre d’or ? On a l’encadrement très grossier 1 < phi < 2 que l'on peut écrire 1/1 < phi < 2/1 histoire de faire apparaître clairement des ratios. Je vais donc vous livrer une astuce qui doit dater de la nuit des temps vu sa simplicité : on additionne les numérateurs ensemble et les dénominateurs ensemble et on obtient la fraction 3/2 qui est plus petite que phi d'où un nouvel encadrement 3/2 < phi < 2/1 et on peut recommencer mais là 5/3 est plus grand que phi. Comme phi est irrationnel cela peut se poursuivre à l'infini (avec des entiers qui deviennent vite astronomiques) et phi possède la propriété unique d'alterner un coup plus petit un coup plus grand et en fait on est en lien directement avec les convergents de la fraction continue de phi qui sont les fractions successives obtenues et améliorant l'encadrement. Donc les propriétés arithmétiques de phi via ce genre d'algorithme (que j'appelle algorithme d'approximation continue car pour tout autre nombre compris entre 1 et 2 il est très lié à la fraction continue associée au nombre étudié en donnant les convergents quand on se met à basculer de l'autre côté du nombre étudié) ont pu interpeler certains anciens (ceux aptes au calcul de rationnels) vu que la bascule se produit à chaque pas. Vous retrouvez bien sur avec les dénominateurs la suite de Fibonacci et vous n'avez pas besoin de connaître réellement phi qui est la limite de ce processus et comme personne n'est immortel… (et que la notion topologique de limite a quand même mis du temps à se bâtir) il a bien fallu se contenter d'approximations. Maintenant au delà de l'histoire de savoir si le mètre a été inventé dans des temps immémoriaux, il est probable que les égyptiens avaient compris que le rapport pi/phi^2 était très voisin de 6/5 = 1,2, ou du moins (les petits malins qui ont bâti des pyramides) que l'on pouvait imaginer que pi était les 6/5ième de phi^2 donc un nombre rationnel. Comme ces petits malins savaient manier l'algorithme que j'appelle d'approximation continue, ils ont pu vouloir l'appliquer à la moitié de 6/5(phi+1) donc 3/5x(phi+1) qui est bien un nombre compris entre 1 et 2. Evidemment cela dépend de la fraction que l'on prend pour phi, mais je ne vais pas entrer dans les détails notre “pi d'or“ donne 3/2 qui est en dessous puis 5/3 et encore 8/5 au dessus puis 11/7 (la moitié de 22/7 bien évidemment) toujours au dessus avant de basculer (donc 11/7 est un convergent) en dessous avec 14/9 d'où l'encadrement 14/9 < pidor < 11/7 et là on va mouliner un moment dessous jusqu'à obtenir 366/233 puis on passe au dessus avec 377/230 ce qui fait que 366/233 est un convergent. Tiens donc 366/233 est un convergent pas défaut de pidor et 377/233 un convergent par défaut de phi ; il y a de quoi surprendre nos petits malins même s'il n'y avait pas lieu (ce sont des nombres aussi quelconques que les autres), et du coup phi c'est 377/233 et pi c'est 366/233. La carré de phi c'est alors 610/233 donc phi+1 et donc le rapport pidor/phi2 vaut bien 3/5. Pi vaut alors 732/233 = 3,141630 ce qui est une approximation remarquable – et on pouvait laisser 22/7 aux scribouillards – et pi/6 = 0,52360 tandis que phi/5 = 0,52360 pareil forcément et le tour est joué, si le diamètre du cercle est l'unité. Mais évidemment l'unité c'est la coudée de Pharaon et il en a fallu en prendre une fraction pour avoir le rayon du cercle, et selon les coudées royales ce rayon a varié dans les mêmes proportions en restant autour du demi-mètre actuel ce qui pouvait bien sûr correspondre à une fraction remarquable d'une “unité astronomique terrestre“. Il faut bien sûr penser que phi en tant que rapport privilégié (phi = 377/233 ; phi – 1 = 144/233 ; phi +1 = 610/233) était en effet plus important que pi sur le plan des rapports architecturaux et de la solidité des édifices sans doute aussi, même si cette valeur de pi a aussi pu servir (c'est mieux que le 22/7 des arpenteurs et surtout que le 256/81 ou même le 3 biblique) . Est-ce cela le “secret des pyramides“ qui visiblement n'a pas été transmis en dehors d'un cercle très restreint ? Au sujet de 440 coudées donc surtout de 44 (dizaines de coudées) il faut savoir que (64/63)^44 c'est quasiment 2. Est-ce un clin d'oeil à ce savoir ? Vous noterez aussi que 64/57 à la puissance 6 c'est aussi quasiment 2 (musicalement pour un luthier cela correspond à peu près au ton égal même si 55/49 est meilleur, mais partager un tube en 64 parties égales est plus simple qu'en 55 du moins dans des temps plus reculés encore, et la différence est imperceptible. L'aire avantage de 64/57 c'est que dans un même tracé vous avez aussi la quinte du ton 64/38 = 32/19. Si le luthier répète l'opération il obtient le diton égale et sa quinte, puis le triton égal et sa quinte qui faut ramener dans l'octave en la doublant… et in fine il parvient à l'octave, la moitié de la taille du tube de départ, et à sa quinte comme quoi ce système qui fonde d'ailleurs la double gamme à six tons chinoise a pu émerger il y a très longtemps, sans que l'on ne s'étonne du fait que Jean de BEAUGRAND à la demande du père Marin MERSENNE, a cru bon calculer la “onzième proportionnelle“ autrement dit la racine douzième de deux – et je sais pas si le geostaticien comme le dénommait DESCARTES a usé de la méthode d'approximation continue pour trouver des encadrements par des ratios convergents). Voilà bonne réflexion !
Euzenius de Fribourg
[…] y a des nombres qu'on retrouve partout… une proportion divine ? un nombre divin… c'est la base de la structure de […]
[…] système de "quine des bâtisseurs" (aussi appelé parfois "pige des bâtisseurs" ) est construit sur la base d'une division en […]
[…] personnellement aussi tenté de reprendre les calculs de Paucton, mais bien que le ordres de grandeurs soit souvent assez juste, je ne trouve rien qui colle […]
J’ai recalculé Pi, qui vaut 3,14164, a partir de la coudée egyptienne. Ca vous interesse? Deux pages limpides
Bonjour, merci pour votre commentaire.
C’est intriguant. Ce n’est pas la valeur de π qui est généralement acceptée.
Quelle valeur de coudées utilisez vous ?
Moi j’en vois deux versions.
Donc si vous dites avoir 2 pages limpides… pourquoi pas 🙂
Merci
M.Martouf
–,, proporrei qui, se mi è consentito , di considerare sia M.Eugenio di Friburgo si M.
M.Huart,che hanno esaminato egregiamente la contiguità spirituale di 𝝿 e di 𝞅.
Rammento che in passato avevo trattato le Nombre d’Or sul quale propongo un approccio che risale a Pitagora ma anche alla formula del 𝝿.
Vediamo 𝞅 che dipende dalla tripla pitagorica .
𝞅= A/P±√(c/b) dove A e P sono area e perimetro del triangolo retto (3-4-5) mentre
c et b sono lìipotenusa e cateto lungo del triangolo stesso.
𝞅=6/12±√5/4= 1/2±√1,25 = 0,5±1,118033989..= (1,618..) est (-0,618..)
Dallo stesso triangolo si ottiene 𝞅=∛(b+tg(𝛃/b) dove b è il cateto lungo et 𝛃 è l’angolo opposto al cateto lungo(b).;quindi 𝞅=∛4+(0,236067977)=∛4,236067977=
1,618033989..
In buona sostanza abbiamo scoperto che 𝞅 non è solo un rapporto euclideo fra due lunghezze la cui somma è uguale ad 1 ma anche che 𝞅 è in rapporto indiretto con l’angolo acuto opposto al cateto lungo del triangolo pitagorico.
E, riguardo a questo Pitagora ( si racconta oralmente e non lo troverete mai per iscritto che 𝝿 =355/113(frazione generatrice ).Ma qui i critici che non mancano mai chiederebbero come vi è arrivato Pitagora ancor prima dei cinesi?
Ecco qua:𝝿= a+( b^2/(a+b)^2+(b+c)^2 che sviluppato ,offre;>>
𝝿= 3+4^2/( 3+4)^2+(3+5)^2>>= 3+16/(49+64)= 3+16/113= 355/113 ma Pitagora voleva che 𝝿 derivasse da Numeri primi ed ecco che 𝝿=( 5*71/113).
Da quanto abbiamo esaminato possiamo tranquillamente affermare che i Cinesi ebbero per vie traverse nel quarto secolo ciò che Pitagora 1000anni prima aveva appreso dalla ceto sacerdotale delle culture mesopotamiche ed egizia.
Cordialità
Joseph11
La solution c »est un triangle rectangle de côtés 1 , 2 , et hypothenuse Racine de 5
Total = 5,236 soit 2 Phi² et 10 coudées
Pi = 6 * ( Phi² / 5 )
= 3,141640782 sans problèmes de décimales
OK, je vous que vous avez choisi la version de la coudée que j’appelle « masculine », car prise à partir du triangle formé par la coupe en deux par a diagonale d’un double carré.
Mais pour moi il y a aussi la version féminine, la version de la coudée prise à partir du cercles divisé en 6 (soit au compas l’écartement du rayon du cercle)
Les deux versions de la coudées royale égyptienne sont:
– coudée royale égyptienne = π/6 en mètre = (φ2)/5 => 0,523598…. → soit le 1/6ème de la circonférence d’un cercle de 1 mètre de diamètre.
– coudée royale égyptienne = (1+2+√5)/10 en mètre => 0,523606… → 1/10 du périmètre du triangle de l’équerre des bâtisseurs en mètre (triangle rectangle dont l’hypoténuse est la diagonale d’un double carré.)
On a donc une proposition de π qui est similaire et utilisable dans la plupart des calculs. Mais tout de même, je ne vois pas comment choisir une définition ou une autre de la coudée !
Tant qu’à faire autant utiliser 22/7 comme approximation de π.
π est une nombre transcendant, et c’est ça qui le rend intéressant. Puis on peut le dessiner en l’approchant par la racine de phi. Mais π reste indessinable.. Une perfection à atteindre, mais impossible à toucher dans le réel.
A méditer
Messieur , Le Grand Martouf,
Mi consenta di proporle come trovare dove si siano nascosti i due numeri sacri , ovvero il binomio Sacro(𝞅;𝝿).
Consideri il triangolo retto (3-4-5) inscritto nel semi-cerchio di diametro c=5
La proiezione del cateto (a=3), sul diametro ,vale 1,8 .
Poi considerando il primo teorema di Euclide ,
la diagonale del rettangolo (1,8*5)=9 =3^2
vale >> √(28,24)=5,314132102
Sottraendo alla diagonale il diametro (5) si ha 0,314132102 =(𝝿/10 )da cui
𝝿= 3,141 132 102 ,che è un valore molto preciso per i tempi di Pitagora.
Infatti il rapporto fra 𝚷 delle calcolatrici e 𝝿 calcolato si ha 𝚷/𝝿 =1,000086..
Questa scoperta la possiamo attribuire al secondo teorema di Pitagora che non fu mai scoperto ma che mi prendo l’iniziativa di portarlo a conoscenza dell’Umanità inconsapevole.
Ed ora veniamo allo stesso triangolo retto (3-4-5)
Pitagora aveva in serbo anche questa formula: 𝞅= (c-b)/(c-a)±√(c/b)
= (5-4)/(5-3)±√ 5/4 = 1/2±1,118033989= (1,619033989) e ( -0,618033989)>>𝞅 e (- 1/𝞅)
Cordialità
joseph11
li 5/7/2022
Réponse en trois points :
La coudée ne nécessite pas d’être exprimée en metres. C’est une proportion. Si les pyramides du Caire étaient construites en pieds anglais, elles seraient trois fois plus petites, mais elles auraient les mêmes proportions par rapport à Phi
On peut dessiner Phi, par rapport au rayon d’un cercle. Si l’on prend un compas d’ouverture quelconque, le rayon, et qu’on trace un demi cercle, on trace et on développe bien Pi , qui est 3,141640782 radians (rayon )
Calcul algebrique de Pi :
Considérons un triangle rectangle de côtés 1,2, et donc hypoténuse √5 ( qui satisfait par ailleurs Fibonacci )
Etablissons le périmètre du triangle : 2 + 1 + √5 et divisons le par 10 qui est un nombre comme les 10 doigts de la main.
Prenons-en 6 : on a x= 6* (2+1+√5)/10
Soit en divisant par 2 : x = 6 * (1+ (1+√5)/2)/5 soit x = 6 * (ϕ+1)/5
Soit 6 * ϕ²/5
Vérifions l’application numérique :
X = 6 * ( 2,618033989)/5 → 6* 0,523606797 → 3,141640782
Il existe bien un lien ( contiguita spirituale ) entre π et Phi π = 6* φ²/5
Ces différents calculs sont issus de rapports algébriques, donc parfaitement abstraits.
Vérifions cependant la précision de cette affirmation, en utilisant un grand nombre de décimales de π et de √5 :
Pi vaut donc : 6* 0,523606797 = 3,141640782
et (3,141640782)/(0,523606797 ) = 6 très exactement
Il faut comprendre que dans l’ordre de la ‘’ Création ‘’, ( tout comme dans Fibonacci ), zéro vient en premier, et que passant par un triangle rectangle de cotés 1 et 2, viennent ensuite 1, puis 2, puis 5 sous forme de √5, donc Phi , ( φ= √((5+ √5)/(5- √5)) ) puis arrive seulement π , 6*φ²/5
merci pour vos recherches!
si je peux me permettre une autre approche du calcul de la coudée royale en rapport avec la géométrie des volumes élémentaires. La coudée C est le ratio de la sphère de rayon R (ou diamètre 2R) par la cube de côté 2R. autrement dit la boule s’inscrit le cube. ça donne 4/3Pi R3/8R3 = Pi/6. la coudée est une proportion!
Alors; coudée royale ✍️→ 1/5(𝞿^2)=0,5236
Coudée ordinaire → →1/(𝞿+1/𝞅)= 1/√5= 0,4472.